Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-01T17:45:30.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of Differential Transforms for Heat Semigroups Generated by Schrödinger Operators

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  12 February 2020

Zhang Chao  and
José L. Torrea
Zhang Chao
Affiliation:
School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018, P.R. China email: zaoyangzhangchao@163.com
José L. Torrea
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain email: joseluis.torrea@uam.es
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we analyze the convergence of the following type of series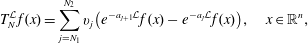

$$\begin{eqnarray}T_{N}^{{\mathcal{L}}}f(x)=\mathop{\sum }_{j=N_{1}}^{N_{2}}v_{j}\big(e^{-a_{j+1}{\mathcal{L}}}f(x)-e^{-a_{j}{\mathcal{L}}}f(x)\big),\quad x\in \mathbb{R}^{n},\end{eqnarray}$$
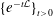where ${\{e^{-t{\mathcal{L}}}\}}_{t>0}$ is the heat semigroup of the operator 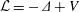${\mathcal{L}}=-\unicode[STIX]{x1D6E5}+V$ with 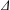$\unicode[STIX]{x1D6E5}$ being the classical laplacian, the nonnegative potential 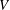$V$ belonging to the reverse Hölder class 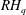$RH_{q}$ with 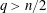$q>n/2$ and 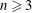$n\geqslant 3$, 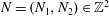$N=(N_{1},N_{2})\in \mathbb{Z}^{2}$ with 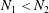$N_{1}<N_{2}$, 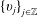${\{v_{j}\}}_{j\in \mathbb{Z}}$ is a bounded real sequences, and 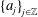${\{a_{j}\}}_{j\in \mathbb{Z}}$ is an increasing real sequence.

Our analysis will consist in the boundedness, in 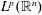$L^{p}(\mathbb{R}^{n})$ and in 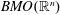$BMO(\mathbb{R}^{n})$, of the operators 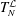$T_{N}^{{\mathcal{L}}}$ and its maximal operator 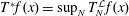$T^{\ast }f(x)=\sup _{N}T_{N}^{{\mathcal{L}}}f(x)$.

It is also shown that the local size of the maximal differential transform operators (with 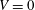$V=0$) is the same with the order of a singular integral for functions 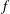$f$ having local support. Moreover, if 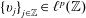${\{v_{j}\}}_{j\in \mathbb{Z}}\in \ell ^{p}(\mathbb{Z})$, we get an intermediate size between the local size of singular integrals and Hardy–Littlewood maximal operator.

Keywords

differential transformheat semigroupSchrödinger operatorLaplacian

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 622 - 655
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Natural Science Foundation of China (Grant Nos. 11971431, 11401525), the Natural Science Foundation of Zhejiang Province (Grant No. LY18A010006), the first Class Discipline of Zhejiang-A (Zhejiang Gongshang University-Statistics) and the State Scholarship Fund (No. 201808330097). The second author was supported by grant PGC2018-099124-B-I00 (MINECO/FEDER) from Government of Spain.

References

Betancor, J. J., Crescimbeni, R., and Torrea, J. L., The 𝜌-variation of the heat semigroup in the Hermitian setting: behaviour in L ∞. Proc. Edinb. Math. Soc. 54(2011), 569–585. https://doi.org/10.1017/S0013091510000556CrossRefGoogle Scholar
Bernardis, A. L., Lorente, M., Martín-Reyes, F. J., Martínez, M. T., de la Torre, A., and Torrea, J. L., Differential transforms in weighted spaces . J. Fourier Anal. Appl. 12(2006), 83–103. https://doi.org/10.1007/s00041-005-5064-zCrossRefGoogle Scholar
Chao, Z., Ma, T., and Torrea, J. L., Boundedness of differential transforms for one-sided fractional Poisson type operator sequence. J. Geom. Anal., to appear. https://arxiv.org/abs/1907.07422Google Scholar
Crescimbeni, R., Macías, R. A., Menárguez, T., Torrea, J. L., and Viviani, B., The 𝜌-variation as an operator between maximal operators and singular integrals. J. Evol. Equ. 9(2009), 81–102. https://doi.org/10.1007/s00028-009-0003-0CrossRefGoogle Scholar
Duoandikoetxea, J., Fourier analysis . Translated and revised from the 1995 Spanish original by David Cruz-Uribe. Graduate Studies in Mathematics, 29, American Mathematical Society, Providence, RI, 2001.Google Scholar
Dziubański, J., Garrigós, G., Martínez, T., Torre, J. L., and Zienkiewicz, J., BMO spaces related to Schrödinger operators with potentials satisfying a reverse Hölder inequality . Math. Z. 249(2005), 329–356. https://doi.org/10.1007/s00209-004-0701-9CrossRefGoogle Scholar
Dziubański, J. and Zienkiewicz, J., H p spaces for Schrödinger operators. In: Fourier analysis and related topics. Banach Center Publ, 56, Polish Acad. Sci. Inst. Math, Warsaw, 2002, pp. 45–53. https://doi.org/10.4064/bc56-0-4Google Scholar
Dziubański, J. and Zienkiewicz, J., H p spaces associated with Schrödinger operators with potentials from reverse Hölder classes . Colloq. Math. 98(2003), 5–38. https://doi.org/10.4064/cm98-1-2CrossRefGoogle Scholar
Jones, R. L. and Rosenblatt, J., Differential and ergodic transforms . Math. Ann. 323(2002), 525–546. https://doi.org/10.1007/s002080200313CrossRefGoogle Scholar
Kato, T., Perturbation theory for linear operators . Grundlehren der Mathematischen Wissenschaften, 132, Springer-Verlag, Berlin-New York, 1976.Google Scholar
Kurata, K., An estimate on the heat kernel of magnetic Schrödinger operators and uniformly elliptic operators with non-negative potentials . J. Lond. Math. Soc. 62(2000), 885–903. https://doi.org/10.1112/S002461070000137XCrossRefGoogle Scholar
Ma, T., Stinga, P., Torrea, J. L., and Zhang, C., Regularity estimates in Hölder spaces for Schrödinger operators via a T1 theorem . Ann. Mat. Pura Appl. 193(2014), 561–589. https://doi.org/10.1007/s10231-012-0291-9CrossRefGoogle Scholar
Ma, T., Torrea, J. L., and Xu, Q., Weighted variation inequalities for differential operators and singular integrals . J. Funct. Anal. 268(2015), 376–416. https://doi.org/10.1016/j.jfa.2014.10.008CrossRefGoogle Scholar
de Francia, J. L. Rubio, Ruiz, F. J., and Torrea, J. L., Calderón–Zygmund theory for operator-valued kernels . Adv. in Math. 62(1986), 7–48. https://doi.org/10.1016/0001-8708(86)90086-1CrossRefGoogle Scholar
Rudin, W., Functional analysis . Second ed., International Series in Pure and Applied Mathematics , McGraw-Hill, Inc., New York, 1991.Google Scholar
Shen, Z., L p estimates for Schrödinger operators with certain potentials . Ann. Inst. Fourier (Grenoble) 45(1995), 513–546.CrossRefGoogle Scholar
Stein, E. M., Topics in harmonic analysis related to the Littlewood-Paley theory . Annals of Mathematics Studies, 63, Princeton University Press, Princeton, NJ, 1970.CrossRefGoogle Scholar