Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-05-31T11:08:12.730Z Has data issue: false hasContentIssue false
  • English
  • Français

Calabi–Yau Quotients of Hyperkähler Four-folds

Part of: Cycles and subschemes Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  15 February 2019

Chiara Camere ,
Alice Garbagnati  and
Giovanni Mongardi
Chiara Camere
Affiliation:
Dipartimento di Matematica, Università degli Studi di Milano, via Cesare Saldini 50, 20133 Milano, Italy Email: chiara.camere@unimi.italice.garbagnati@unimi.it
Alice Garbagnati
Affiliation:
Dipartimento di Matematica, Università degli Studi di Milano, via Cesare Saldini 50, 20133 Milano, Italy Email: chiara.camere@unimi.italice.garbagnati@unimi.it
Giovanni Mongardi
Affiliation:
Dipartimento di Matematica, Alma Mater Studiorum Università di Bologna, Piazza di porta san Donato 5, 40126 Bologna, Italy Email: giovanni.mongardi2@unibo.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to construct Calabi–Yau 4-folds as crepant resolutions of the quotients of a hyperkähler 4-fold 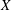$X$ by a non-symplectic involution $\unicode[STIX]{x1D6FC}$. We first compute the Hodge numbers of a Calabi–Yau constructed in this way in a general setting, and then we apply the results to several specific examples of non-symplectic involutions, producing Calabi–Yau 4-folds with different Hodge diamonds. Then we restrict ourselves to the case where 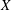$X$ is the Hilbert scheme of two points on a K3 surface 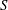$S$, and the involution $\unicode[STIX]{x1D6FC}$ is induced by a non-symplectic involution on the K3 surface. In this case we compare the Calabi–Yau 4-fold 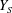$Y_{S}$, which is the crepant resolution of 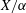$X/\unicode[STIX]{x1D6FC}$, with the Calabi–Yau 4-fold 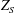$Z_{S}$, constructed from 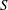$S$ through the Borcea–Voisin construction. We give several explicit geometrical examples of both these Calabi–Yau 4-folds, describing maps related to interesting linear systems as well as a rational 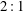$2:1$ map from 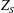$Z_{S}$ to 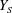$Y_{S}$.

Keywords

irreducible holomorphic symplectic manifoldHyperkähler manifoldCalabi–Yau 4-foldBorcea–Voisin constructionautomorphismquotient mapnon-symplectic involution

MSC classification

Primary: 14J32: Calabi-Yau manifolds
Secondary: 14J35: $4$-folds 14J50: Automorphisms of surfaces and higher-dimensional varieties 14C05: Parametrization (Chow and Hilbert schemes)
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 45 - 92
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author A. G. was partially supported by PRIN 2010-2011: “Geometria delle Varietà Algebriche” and FIRB 2012 “Moduli spaces and their applications”. Author G. M. was supported by FIRB 2012 “Moduli spaces and their applications”.

References

Bǎdescu, L. and Beltrametti, M. C., Seshadri positive submanifolds of polarized manifolds . Cent. Eur. J. Math. 11(2013), no. 3, 447–476. https://doi.org/10.2478/s11533-012-0146-z.Google Scholar
Barth, W. P., Hulek, K., Peters, C. A. M., and Van de Ven, A., Compact complex surfaces, Second ed., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 4, Springer-Verlag, Berlin, 2004.Google Scholar
Batyrev, V. V., Birational Calabi-Yau n-folds have equal Betti numbers . In: New trends in algebraic geometry (Warwick, 1996), London Math. Soc. Lecture Note Ser., 264, Cambridge University Press, Cambridge, 1999, pp. 1–11. https://doi.org/10.1017/CBO9780511721540.002.Google Scholar
Beauville, A., Variétés Kähleriennes dont la premiere classe de Chern est nulle . J. Differential Geom 18(1983), no. 4, 755–782. https://doi.org/10.4310/jdg/1214438181.Google Scholar
Beauville, A., Antisymplectic involutions of holomorphic symplectic manifolds . J. Topol. 4(2011), no. 2, 300–304. https://doi.org/10.1112/jtopol/jtr002.Google Scholar
Bogomolov, F. A., On the decomposition of Kähler manifolds with trivial canonical class . Mat. Sb. (N. S.) 93(135)(1974), no. 4, 573–575, 630.Google Scholar
Boissière, S., Automorphismes naturels de l’espace de Douady de points sur une surface . Canad. J. Math. 64(2012), no. 1, 3–23. https://doi.org/10.4153/CJM-2011-041-5.Google Scholar
Boissière, S., Camere, C., and Sarti, A., Classification of automorphisms on a deformation family of hyper-Kähler four-folds by p-elementary lattices . Kyoto J. Math. 56(2016), no. 3, 465–499. https://doi.org/10.1215/21562261-3600139.Google Scholar
Boissière, S., Nieper-Wiß kirchen, M., and Sarti, A., Higher dimensional Enriques varieties and automorphisms of generalized Kummer varieties . J. Math. Pures Appl. (9) 95(2011), no. 5, 553–563. https://doi.org/10.1016/j.matpur.2010.12.003.Google Scholar
Boissière, S. and Sarti, A., A note on automorphisms and birational transformations of holomorphic symplectic manifolds . Proc. Amer. Math. Soc. 140(2012), no. 12, 4053–4062. https://doi.org/10.1090/S0002-9939-2012-11277-8.Google Scholar
Borcea, C., K3 surfaces with involution and mirror pairs of Calabi–Yau manifolds. Mirror symmetry, II, AMS/IP Stud. Adv. Math., 1, American Mathematical Society, Providence, RI, 1997, pp. 717–743.Google Scholar
Camere, C., Lattice polarized irreducible holomorphic symplectic manifolds . Ann. l’Inst. Fourier (Grenoble) 66(2016), no. 2, 687–709. https://doi.org/10.5802/aif.3022.Google Scholar
Cattaneo, A. and Garbagnati, A., Calabi-Yau 3-folds of Borcea-Voisin type and elliptic fibrations . Tohoku Math. J. (2) 68(2016), no. 4, 515–558. https://doi.org/10.2748/tmj/1486177214.Google Scholar
Cynk, S. and Hulek, K., Higher-dimensional modular Calabi-Yau manifolds . Canad. Math. Bull. 50(2007), no. 4, 486–503. https://doi.org/10.4153/CMB-2007-049-9.Google Scholar
Cynk, S. and van Straten, D., Infinitesimal deformations of double covers of smooth algebraic varieties . Math. Nachr. 279(2006), no. 7, 716–726. https://doi.org/10.1002/mana.200310388.Google Scholar
Debarre, O., Higher-dimensional algebraic geometry. Universitext, Springer-Verlag, New York, 2001. https://doi.org/10.1007/978-1-4757-5406-3.Google Scholar
Denef, J. and Loeser, F., Germs of arcs on singular algebraic varieties and motivic integration . Invent. Math. 135(1999), no. 1, 201–232. https://doi.org/10.1007/s002220050284.Google Scholar
Dillies, J., Generalized Borcea–Voisin construction . Lett. Math. Phys. 100(2012), no. 1, 77–96. https://doi.org/10.1007/s11005-011-0528-3.Google Scholar
Dolgachev, I. V., Mirror symmetry for lattice polarized K3 surfaces . J. Math. Sci. 81(1996), no. 3, 2599–2630. https://doi.org/10.1007/BF02362332.Google Scholar
Esnault, H. and Viehweg, E., Lectures on vanishing theorems. DMV Seminar, 20, Birkhäuser Verlag, Basel, 1992. https://doi.org/10.1007/978-3-0348-8600-0.Google Scholar
Ferretti, A., Special subvarieties of EPW sextics . Math. Z. 272(2012), no. 3–4, 1137–1164. https://doi.org/10.1007/s00209-012-0980-5.Google Scholar
Fujiki, A., On primitively symplectic compact Kähler V-manifolds of dimension four . In: Classification of algebraic and analytic manifolds (Katata, 1982), Progr. Math., 39, Birkhäuser Boston, Boston, MA, 1983, pp. 71–250.Google Scholar
Fujiki, A., Finite automorphism groups of complex tori of dimension two . Publ. Res. Inst. Math. Sci. 24(1988), no. 1, 1–97. https://doi.org/10.2977/prims/1195175326.Google Scholar
Fulton, W., Intersection theory, Second ed., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 2, Springer-Verlag, Berlin, 1998. https://doi.org/10.1007/978-1-4612-1700-8.Google Scholar
Gross, M., Huybrechts, D., and Joyce, D., Calabi–Yau manifolds and related geometries: Lectures at a summer school in Nordfjordeid Norway, June 2001. Universitext, Springer-Verlag, Berlin, 2003. https://doi.org/10.1007/978-3-642-19004-9.Google Scholar
Guan, D., On the Betti numbers of irreducible compact hyperkähler manifolds of complex dimension four . Math. Res. Lett. 8(2001), no. 5–6, 663–669. https://doi.org/10.4310/MRL.2001.v8.n5.a8.Google Scholar
Hassett, B. and Tschinkel, Y., Hodge Theory and Lagrangian planes on generalized Kummer fourfolds . Moscow Math. J. 13(2013), no. 1, 33–56, 189.Google Scholar
Huybrechts, D., Moduli spaces of hyperkähler manifolds and mirror symmetry . In: Intersection theory and moduli, ICTP Lect. Notes, 19, Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2004, pp. 185–247.Google Scholar
Iliev, A., Kapustka, G., Kapustka, M., and Ranestad, K., Hyper-kähler fourfolds and Kummer surfaces . Proc. Lond. Math. Soc. 115(2017), no. 6, 1276–1316. https://doi.org/10.1112/plms.12063.Google Scholar
Ito, T., Birational smooth minimal models have equal Hodge numbers in all dimensions . In: Calabi-Yau varieties and mirror symmetry (Toronto, ON, 2001), Fields Inst. Commun., 38, American Mathematical Society, Providence, RI, 2003, pp. 183–194.Google Scholar
Joyce, D. D., Compact manifolds with special holonomy. Oxford Mathematical Monographs, Oxford University Press, Oxford, 2000.Google Scholar
Kawamata, Y., Flops connect minimal models . Publ. Res. Inst. Math. Sci. 44(2008), no. 2, 419–423. https://doi.org/10.2977/prims/1210167332.Google Scholar
Kawatani, K., On the birational geometry for irreducible symplectic 4-folds related to the Fano schemes of lines. 2009. arxiv:0906.0654.Google Scholar
Kempf, G. R., Algebraic varieties. London Mathematical Society Lecture Note Series, 172, Cambridge University Press, Cambridge, 1993. https://doi.org/10.1017/CBO9781107359956.Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, 134, Cambridge University Press, 1998. https://doi.org/10.1017/CBO9780511662560.Google Scholar
Krug, A., Ploog, D., and Sosna, P., Derived categories of resolutions of cyclic quotient singularities . Q. J. Math. 69(2018), 509–548. https://doi.org/10.1093/qmath/hax048.Google Scholar
Logachev, D., Fano threefolds of genus 6 . Asian J. Math. 16(2012), no. 3, 515–559. https://doi.org/10.4310/AJM.2012.v16.n3.a9.Google Scholar
Menet, G., On the integral cohomology of quotients of manifolds by cyclic groups . J. Math. Pures Appl. (9)(2017) . https://doi.org/10.1016/j.matpur.2017.11.008.Google Scholar
Miranda, R., The basic theory of elliptic surfaces. Dottorato di Ricerca in Matematica. ETS Editrice, Pisa, 1989. http://www.math.colostate.edu/∼miranda/BTES-Miranda.pdf.Google Scholar
Mongardi, G., Tari, K., and Wandel, M., Automorphisms of generalised Kummer fourfolds . Manuscripta Math.(2017) . https://doi.org/10.1007/s00229-017-0942-7.Google Scholar
Mongardi, G. and Wandel, M., Induced automorphisms on irreducible symplectic manifolds . J. Lond. Math. Soc. (2) 92(2015), no. 1, 123–143. https://doi.org/10.1112/jlms/jdv012.Google Scholar
Nikulin, V. V., Kummer surfaces . Izv. Akad. Nauk SSSR Ser. Mat. 39(1975), no. 2, 278–293, 471.Google Scholar
Nikulin, V. V., Finite groups of automorphisms of Kählerian K3 surfaces . Trudy Moskov. Mat. Obshch. 38(1979), 75–137.Google Scholar
Nikulin, V. V., Involutions of integral quadratic forms and their applications to real algebraic geometry . Izvestiya: Mathematics 22(1984), no. 1, 99–172.Google Scholar
O’Grady, K. G., Irreducible symplectic 4-folds and Eisenbud-Popescu-Walter sextics . Duke Math. J. 134(2006), no. 1, 99–137. https://doi.org/10.1215/S0012-7094-06-13413-0.Google Scholar
Oguiso, K., No cohomologically trivial non-trivial automorphism of generalized Kummer manifolds. 2012. arxiv:1208.3750.Google Scholar
Oguiso, K., On Jacobian fibrations on the Kummer surfaces of the product of nonisogenous elliptic curves . J. Math. Soc. Japan 41(1989), no. 4, 651–680. https://doi.org/10.2969/jmsj/04140651.Google Scholar
Oguiso, K., On automorphisms of the punctual Hilbert schemes of K3 surfaces . Eur. J. Math. 2(2016), no. 1, 246–261. https://doi.org/10.1007/s40879-015-0070-4.Google Scholar
Oguiso, K. and Schröer, S., Enriques manifolds . J. Reine Angew. Math. 661(2011), 215–235. https://doi.org/10.1515/CRELLE.2011.077.Google Scholar
Ohashi, H. and Wandel, M., Non-natural non-symplectic involutions on symplectic manifolds of $K3^{[2]}$ -type. 2013. arxiv:1305.6353.Google Scholar
Saint-Donat, B., Projective models of K - 3 surfaces . Amer. J. Math. 96(1974), 602–639. https://doi.org/10.2307/2373709.Google Scholar
Sawon, J., Abelian fibred holomorphic symplectic manifolds . Turkish J. Math. 27(2003), no. 1, 197–230.Google Scholar
van Geemen, B., Some remarks on Brauer groups of K3 surfaces . Adv. Math. 197(2005), no. 1, 222–247. https://doi.org/10.1016/j.aim.2004.10.004.Google Scholar
Voisin, C., Miroirs et involutions sur les surfaces K3 . Journées de Géométrie Algébrique d’Orsay (Orsay, 1992). Astérisque 218(1993), 273–323.Google Scholar
Voisin, C., Hodge theory and complex algebraic geometry. I. Cambridge Studies in Advanced Mathematics, 76, Cambridge University Press, Cambridge, 2002. https://doi.org/10.1017/CBO9780511615344.Google Scholar
Wang, C.-L., Cohomology theory in birational geometry . J. Differential Geom. 60(2002), no. 2, 345–354. https://doi.org/10.4310/jdg/1090351105.Google Scholar