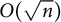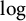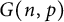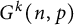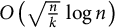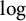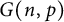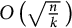1 Introduction and results
1.1 Motivation
The game of Cops and Robber was introduced by Quilliot [Reference Quilliot25] and independently by Nowakowski and Winkler [Reference Nowakowski and Winkler23]. It is a two-player game played on a simple connected graph
![]() $G= (V,E)$
, with one player controlling a set of m cops and the other player controlling a single robber. For convenience, we will sometimes refer to the cops and the robber as pieces. At the start of the game, the first player chooses a starting vertex for each of the cops, then the second player chooses a starting vertex for the robber. Subsequently, the players take alternating turns and in each turn a player can move each of their pieces to an adjacent vertex (i.e., the pieces move along the edges of G). Note that more than one cop can simultaneously occupy a single vertex and that not every piece must be moved in every turn. The position of all the pieces is known to both players throughout the game. The cops win if at some point in the game a cop occupies the same vertex as the robber, otherwise the robber wins. As this is a game with full information, for each graph G and each number of initial cops m, one of the two players has a winning strategy. The cop number
$G= (V,E)$
, with one player controlling a set of m cops and the other player controlling a single robber. For convenience, we will sometimes refer to the cops and the robber as pieces. At the start of the game, the first player chooses a starting vertex for each of the cops, then the second player chooses a starting vertex for the robber. Subsequently, the players take alternating turns and in each turn a player can move each of their pieces to an adjacent vertex (i.e., the pieces move along the edges of G). Note that more than one cop can simultaneously occupy a single vertex and that not every piece must be moved in every turn. The position of all the pieces is known to both players throughout the game. The cops win if at some point in the game a cop occupies the same vertex as the robber, otherwise the robber wins. As this is a game with full information, for each graph G and each number of initial cops m, one of the two players has a winning strategy. The cop number
![]() $c(G)$
of a graph G is defined as the minimum number
$c(G)$
of a graph G is defined as the minimum number
![]() $m \in \mathbb {N}$
such that m cops have a winning strategy on G. The cop number has been extensively studied since the introduction of this game.
$m \in \mathbb {N}$
such that m cops have a winning strategy on G. The cop number has been extensively studied since the introduction of this game.
While there is a structural characterization of the graphs with cop number 1 [Reference Nowakowski and Winkler23], in general the problem of determining the cop number of a graph is EXPTIME-complete [Reference Kinnersley19], and so research in this area has been focused on bounding the cop number of particular graph classes. For example, a classic result of Aigner and Fromme [Reference Aigner and Fromme2] shows that the cop number of a connected planar graph is at most 3. More generally, it is known that the cop number is bounded for any proper minor-closed class of graphs [Reference Andreae3], and there has been much research into determining the largest cop number of a graph that can be embedded in a fixed surface [Reference Bowler, Erde, Lehner and Pitz7, Reference Clarke, Fiorini, Joret and Theis11, Reference de la Maza, Hosseini, Knox, Mohar and Reed22, Reference Iršič, Mohar and Wesolek17, Reference Quilliot26, Reference Schroeder27].
Perhaps the most well-known conjecture in this area is Meyniel’s conjecture (communicated by Frankl [Reference Frankl13]).
Conjecture 1.1 Let G be a connected graph on n vertices. Then
![]() $c(G) = O\left (\sqrt {n}\right )$
.
$c(G) = O\left (\sqrt {n}\right )$
.
Despite much interest in this conjecture, there has been relatively little improvement to the trivial bound of
![]() $O(n)$
. Frankl [Reference Frankl13] gave the first nontrivial upper bound on the cop number of
$O(n)$
. Frankl [Reference Frankl13] gave the first nontrivial upper bound on the cop number of
![]() $O\left (\frac {n \log \log n}{\log n}\right )$
, and this bound was improved to
$O\left (\frac {n \log \log n}{\log n}\right )$
, and this bound was improved to
![]() $O\left (\frac {n}{\log n}\right )$
by Chiniforooshan [Reference Chiniforooshan10]. As of today, the best known general upper bound on the cop number is
$O\left (\frac {n}{\log n}\right )$
by Chiniforooshan [Reference Chiniforooshan10]. As of today, the best known general upper bound on the cop number is
![]() $n 2^{-(1+o(1)) \sqrt {\log n}}$
, given independently by Lu and Peng [Reference Lu and Peng20] and by Scott and Sudakov [Reference Scott and Sudakov28], which was later generalized to different variations of the Cops and Robber game by Frieze, Krivelevich, and Loh [Reference Frieze, Krivelevich and Loh14]. We note that this bound is still
$n 2^{-(1+o(1)) \sqrt {\log n}}$
, given independently by Lu and Peng [Reference Lu and Peng20] and by Scott and Sudakov [Reference Scott and Sudakov28], which was later generalized to different variations of the Cops and Robber game by Frieze, Krivelevich, and Loh [Reference Frieze, Krivelevich and Loh14]. We note that this bound is still
![]() $\Omega \left (n^{1-o(1)} \right )$
, and it remains an open question as to whether the cop number can be bounded by
$\Omega \left (n^{1-o(1)} \right )$
, and it remains an open question as to whether the cop number can be bounded by
![]() $O\left (n^{1-\epsilon }\right )$
for any fixed
$O\left (n^{1-\epsilon }\right )$
for any fixed
![]() $\epsilon>0$
[Reference Baird and Bonato4].
$\epsilon>0$
[Reference Baird and Bonato4].
A natural step toward understanding Conjecture 1.1 is to consider the cop number of the binomial random graph
![]() $G(n,p)$
. For p constant, it was shown by Bonato, Hahn, and Wang [Reference Bonato, Hahn and Wang6] that whpFootnote
1
the cop number of
$G(n,p)$
. For p constant, it was shown by Bonato, Hahn, and Wang [Reference Bonato, Hahn and Wang6] that whpFootnote
1
the cop number of
![]() $G(n,p)$
is logarithmic in n, and hence Conjecture 1.1 holds for almost all graphs. However, if we let p vary as a function of n, then more interesting behavior can be seen to develop. Indeed, Łuczak and Prałat [Reference Łuczak and Prałat21] showed that the cop number of
$G(n,p)$
is logarithmic in n, and hence Conjecture 1.1 holds for almost all graphs. However, if we let p vary as a function of n, then more interesting behavior can be seen to develop. Indeed, Łuczak and Prałat [Reference Łuczak and Prałat21] showed that the cop number of
![]() $G(n,p)$
behaves in a rather interesting manner in dense regimes. Their result can be roughly summarized as follows, where we use
$G(n,p)$
behaves in a rather interesting manner in dense regimes. Their result can be roughly summarized as follows, where we use
![]() $\tilde {\Theta }(\cdot )$
to indicate a bound which holds up to logarithmic factors.
$\tilde {\Theta }(\cdot )$
to indicate a bound which holds up to logarithmic factors.
Theorem 1.2 [Reference Łuczak and Prałat21, Theorem 1.1]
Let
![]() $0 < \alpha <1$
and
$0 < \alpha <1$
and
![]() $d = np = n^{\alpha +o(1)}$
.
$d = np = n^{\alpha +o(1)}$
.
-
(1) If
 $\frac {1}{2j+1} < \alpha < \frac {1}{2j}$
, for some
$\frac {1}{2j+1} < \alpha < \frac {1}{2j}$
, for some
 $j \in \mathbb {N}$
, then whp
$j \in \mathbb {N}$
, then whp  $$ \begin{align*} c\left(G(n,p)\right) = \Theta\left(d^j\right). \end{align*} $$
$$ \begin{align*} c\left(G(n,p)\right) = \Theta\left(d^j\right). \end{align*} $$
-
(2) If
 $\frac {1}{2j} < \alpha < \frac {1}{2j-1}$
, for some
$\frac {1}{2j} < \alpha < \frac {1}{2j-1}$
, for some
 $j \in \mathbb {N}$
, then whp
$j \in \mathbb {N}$
, then whp  $$ \begin{align*} c\left(G(n,p)\right) = \tilde{\Theta}\left(\frac{n}{d^j} \right). \end{align*} $$
$$ \begin{align*} c\left(G(n,p)\right) = \tilde{\Theta}\left(\frac{n}{d^j} \right). \end{align*} $$
In particular, Theorem 1.2 implies that the function
![]() $f\colon (0,1) \to \mathbb {R}$
, defined as
$f\colon (0,1) \to \mathbb {R}$
, defined as
 $$ \begin{align} f(x) = \frac{\log \left( \bar{c}\left(G \left(n,n^{x-1}\right) \right)\right)}{\log n}, \end{align} $$
$$ \begin{align} f(x) = \frac{\log \left( \bar{c}\left(G \left(n,n^{x-1}\right) \right)\right)}{\log n}, \end{align} $$
where
![]() $\bar {c}$
denotes the median of the cop number, has a characteristic zigzag shape (see Figure 1).
$\bar {c}$
denotes the median of the cop number, has a characteristic zigzag shape (see Figure 1).

Figure 1: Zigzag shape of the function f.
In particular, Theorem 1.2 implies that whp
![]() $c\left (G(n,p)\right ) = \tilde {O}\left (\sqrt {n}\right )$
throughout this range of p and that conversely there are choices of p where whp
$c\left (G(n,p)\right ) = \tilde {O}\left (\sqrt {n}\right )$
throughout this range of p and that conversely there are choices of p where whp
![]() $c\left (G(n,p)\right ) = \tilde {\Theta }\left (\sqrt {n}\right )$
and Conjecture 1.1 is close to tight for almost all graphs of this density. Note that, although Theorem 1.2 does not explicitly deal with the case
$c\left (G(n,p)\right ) = \tilde {\Theta }\left (\sqrt {n}\right )$
and Conjecture 1.1 is close to tight for almost all graphs of this density. Note that, although Theorem 1.2 does not explicitly deal with the case
![]() $d = n^{\frac {1}{k} + o(1)}$
with
$d = n^{\frac {1}{k} + o(1)}$
with
![]() $k \in \mathbb {N}$
, the proofs for the upper bounds in [Reference Łuczak and Prałat21] also cover this case, and the authors indicate how to extend the lower bound to this range of d. Bollobás, Kun, and Leader [Reference Bollobás, Kun and Leader5] gave a similar bound which holds also for sparser regimes of p.
$k \in \mathbb {N}$
, the proofs for the upper bounds in [Reference Łuczak and Prałat21] also cover this case, and the authors indicate how to extend the lower bound to this range of d. Bollobás, Kun, and Leader [Reference Bollobás, Kun and Leader5] gave a similar bound which holds also for sparser regimes of p.
Meyniel’s conjecture was finally resolved for all random graphs above the connectedness threshold by Prałat and Wormald [Reference Prałat and Wormald24]. In fact, their result holds for all random graphs with density above
![]() $\frac {1}{2} \log n$
.
$\frac {1}{2} \log n$
.
Theorem 1.3 [Reference Prałat and Wormald24, Theorem 1.2]
Let
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $p(n-1) \geq \left (\frac {1}{2} +\epsilon \right )\log n $
. Then whp
$p(n-1) \geq \left (\frac {1}{2} +\epsilon \right )\log n $
. Then whp
In this paper, we consider a variant of the Cops and Robber game on hypergraphs, and in particular k-uniform hypergraphs, which we call k-graphs, for
![]() $k \in \mathbb {N}_{\geq 2}$
. The game is defined analogously to the
$k \in \mathbb {N}_{\geq 2}$
. The game is defined analogously to the
![]() $2$
-graph case, with the only difference being that the pieces move along hyperedges instead of edges. For the sake of brevity, when it is clear from the context that we are talking about a hypergraph, we will refer to hyperedges as simply edges. Similarly to
$2$
-graph case, with the only difference being that the pieces move along hyperedges instead of edges. For the sake of brevity, when it is clear from the context that we are talking about a hypergraph, we will refer to hyperedges as simply edges. Similarly to
![]() $2$
-graphs, we define the cop number of a hypergraph H to be
$2$
-graphs, we define the cop number of a hypergraph H to be
This game was first considered by Gottlob, Leone, and Scarcello [Reference Gottlob, Leone and Scarcello15] and by Adler [Reference Adler1]. For more recent results on the hypergraph game, we refer the reader to [Reference Siriwong, Boonklurb, Liu and Singhun29], where some classic results on the cop number of
![]() $2$
-graphs are generalized to this setting.
$2$
-graphs are generalized to this setting.
Note that by replacing every edge in a hypergraph by a clique, we arrive at an equivalent
![]() $2$
-graph game on the same vertex set. Thus, the game of Cops and Robber on hypergraphs is equivalent to the
$2$
-graph game on the same vertex set. Thus, the game of Cops and Robber on hypergraphs is equivalent to the
![]() $2$
-graph game played on a restricted class of graphs. On the other hand, we can transform a graph G into a
$2$
-graph game played on a restricted class of graphs. On the other hand, we can transform a graph G into a
![]() $2k$
-uniform hypergraph H with
$2k$
-uniform hypergraph H with
![]() $c(G) = c\left (H\right )$
via a simple blow-up construction: We replace each vertex v in G by k vertices
$c(G) = c\left (H\right )$
via a simple blow-up construction: We replace each vertex v in G by k vertices
![]() $\{v_1,v_2,\ldots v_k\}$
and form a hypergraph
$\{v_1,v_2,\ldots v_k\}$
and form a hypergraph
![]() $H = H(G)$
on
$H = H(G)$
on
![]() $\{ v_i \colon v\in V(G), i \in [k]\}$
by taking an edge of the form
$\{ v_i \colon v\in V(G), i \in [k]\}$
by taking an edge of the form
![]() $\{u_1,u_2,\ldots , u_k, v_1,v_2,\ldots ,v_k\}$
for each edge
$\{u_1,u_2,\ldots , u_k, v_1,v_2,\ldots ,v_k\}$
for each edge
![]() $e=\{u,v\}$
of G (see Figure 2). It is then easy to check that
$e=\{u,v\}$
of G (see Figure 2). It is then easy to check that
![]() $c(G) = c\left (H\right )$
, and moreover
$c(G) = c\left (H\right )$
, and moreover
![]() $|V(H)| = k |V(G)|$
.
$|V(H)| = k |V(G)|$
.

Figure 2: An example of the blow-up construction to generate a
![]() $2k$
-graph H from a
$2k$
-graph H from a
![]() $2$
-graph that has the same cop number. In this case,
$2$
-graph that has the same cop number. In this case,
![]() $k = 5$
,
$k = 5$
,
![]() $|V(H)| = 20$
and
$|V(H)| = 20$
and
![]() $c\left (H\right ) = 2$
.
$c\left (H\right ) = 2$
.
From these two observations, it is easy to see that the following holds:
 $$ \begin{align} \max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|=\frac{2n}{k} \right\} &\leq \max_{} \left\{ c\left(H\right) \colon H \text{ a }k\text{-graph }, |V(H)| = n \right\} \\ &\leq \max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|=n \right\}\!. \nonumber \end{align} $$
$$ \begin{align} \max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|=\frac{2n}{k} \right\} &\leq \max_{} \left\{ c\left(H\right) \colon H \text{ a }k\text{-graph }, |V(H)| = n \right\} \\ &\leq \max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|=n \right\}\!. \nonumber \end{align} $$
In particular, as there are graphs with
![]() $c(G) = \Omega \left (\sqrt {n}\right )$
, there are also k-graphs with
$c(G) = \Omega \left (\sqrt {n}\right )$
, there are also k-graphs with
![]() $c\left (H\right ) = \Omega \left (\sqrt {\frac {n}{k}}\right )$
. It would seem surprising that such a simple construction, which is essentially graphical in nature, could capture the worst-case behavior for the cop number in hypergraphs of higher uniformity, but we conjecture that this bound is in fact tight.
$c\left (H\right ) = \Omega \left (\sqrt {\frac {n}{k}}\right )$
. It would seem surprising that such a simple construction, which is essentially graphical in nature, could capture the worst-case behavior for the cop number in hypergraphs of higher uniformity, but we conjecture that this bound is in fact tight.
Conjecture 1.4 Let H be a connected k-graph on n vertices. Then
![]() $c\left (H\right ) = O\left (\sqrt {\frac {n}{k}}\,\right )$
.
$c\left (H\right ) = O\left (\sqrt {\frac {n}{k}}\,\right )$
.
Clearly, Conjecture 1.4 is a generalization of Meyniel’s conjecture, but we note further that for any polynomial function
![]() $k:=k(n) = n^{\alpha }$
with
$k:=k(n) = n^{\alpha }$
with
![]() $\alpha <1$
, Conjecture 1.4 implies Meyniel’s conjecture. Indeed, if
$\alpha <1$
, Conjecture 1.4 implies Meyniel’s conjecture. Indeed, if
![]() $c\left (H\right ) = O\left (\sqrt {\frac {n}{k(n)}}\right ) = O\left (n^{\frac {1-\alpha }{2}} \right )$
for all n-vertex
$c\left (H\right ) = O\left (\sqrt {\frac {n}{k(n)}}\right ) = O\left (n^{\frac {1-\alpha }{2}} \right )$
for all n-vertex
![]() $n^{\alpha }$
-graphs, then by (1.2),
$n^{\alpha }$
-graphs, then by (1.2),
 $$\begin{align*}&\max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|= 2m \right\} \\&\quad\leq \max_{} \left\{ c\left(H\right) \colon H \text{ a }m^{\frac{\alpha}{1-\alpha}}\text{-graph }, |V(H)| = m^{\frac{1}{1-\alpha}} \right\} \leq O\left(\sqrt{m} \right). \end{align*}$$
$$\begin{align*}&\max_{} \left\{ c\left(G\right) \colon G \text{ a graph }, |V(G)|= 2m \right\} \\&\quad\leq \max_{} \left\{ c\left(H\right) \colon H \text{ a }m^{\frac{\alpha}{1-\alpha}}\text{-graph }, |V(H)| = m^{\frac{1}{1-\alpha}} \right\} \leq O\left(\sqrt{m} \right). \end{align*}$$
As with Meyniel’s Conjecture, a first step toward Conjecture 1.4 is to consider the behavior of the cop number of random k-graphs.
1.2 Main results
The k-uniform binomial random hypergraph, which we denote by
![]() $G^k(n,p)$
, is a random k-graph with vertex set
$G^k(n,p)$
, is a random k-graph with vertex set
![]() $[n]$
in which each edge, that is, each subset of
$[n]$
in which each edge, that is, each subset of
![]() $[n]$
of size k, appears independently with probability p. Although the main focus of this paper is
$[n]$
of size k, appears independently with probability p. Although the main focus of this paper is
![]() $G^k(n,p)$
, the strategies we develop for the cops work in a more general class of k-graphs, those satisfying certain expansion properties.
$G^k(n,p)$
, the strategies we develop for the cops work in a more general class of k-graphs, those satisfying certain expansion properties.
Very roughly, if we denote by
![]() $N^r_V(v)$
the vertices that are at most at a fixed distance r from v, then in
$N^r_V(v)$
the vertices that are at most at a fixed distance r from v, then in
![]() $G^k(n,p)$
we expect this set to be growing exponentially quickly in r, with its size tightly concentrated around its expectation. Furthermore, for different vertices v and w, we do not expect the neighborhoods
$G^k(n,p)$
we expect this set to be growing exponentially quickly in r, with its size tightly concentrated around its expectation. Furthermore, for different vertices v and w, we do not expect the neighborhoods
![]() $N^r_V(v)$
and
$N^r_V(v)$
and
![]() $N^r_V(w)$
to have a large intersection, and so, for small subsets
$N^r_V(w)$
to have a large intersection, and so, for small subsets
![]() $A \subseteq [n]$
, we expect the number of vertices at most at a fixed distance r from A to be around
$A \subseteq [n]$
, we expect the number of vertices at most at a fixed distance r from A to be around
![]() $|A|$
times the size of
$|A|$
times the size of
![]() $N^r_V(v)$
. Similarly, we expect the set of edges
$N^r_V(v)$
. Similarly, we expect the set of edges
![]() $N^r_E(v)$
at most at a fixed distance
$N^r_E(v)$
at most at a fixed distance
![]() $r-1$
from v to be growing at some uniform exponential rate, and for ranges of p where the random hypergraph is sparse enough, and so few pairs of edges have a large intersection, this rate of growth should be roughly
$r-1$
from v to be growing at some uniform exponential rate, and for ranges of p where the random hypergraph is sparse enough, and so few pairs of edges have a large intersection, this rate of growth should be roughly
![]() $\frac {1}{k}$
times that of the vertex-neighborhoods.
$\frac {1}{k}$
times that of the vertex-neighborhoods.
Informally, given
![]() ${\xi }>0$
, we say that a graph is
${\xi }>0$
, we say that a graph is
![]() $\xi $
-expanding if the sizes of its vertex and edge-neighborhoods have this uniform exponential growth, up to some multiplicative error in terms of
$\xi $
-expanding if the sizes of its vertex and edge-neighborhoods have this uniform exponential growth, up to some multiplicative error in terms of
![]() ${\xi }$
. See Definition 2.1 for a precise definition of this notion.
${\xi }$
. See Definition 2.1 for a precise definition of this notion.
Our first result supports Conjecture 1.4 up to a
![]() $\log $
-factor for k-graphs that are
$\log $
-factor for k-graphs that are
![]() $\xi $
-expanding for a fixed expansion constant
$\xi $
-expanding for a fixed expansion constant
![]() ${\xi }$
.
${\xi }$
.
Theorem 1.5 Let
![]() $k \in \mathbb {N}_{\geq 2}$
, let
$k \in \mathbb {N}_{\geq 2}$
, let
![]() ${\xi }>0$
and let G be a
${\xi }>0$
and let G be a
![]() $\xi $
-expanding k-graph on n vertices. Then
$\xi $
-expanding k-graph on n vertices. Then
In fact, depending on the relationship between the average degree d of the hypergraph, its uniformity k, and its order n, we can give a more refined bound for the cop number of a
![]() $\xi $
-expanding hypergraph.
$\xi $
-expanding hypergraph.
Theorem 1.6 Let
![]() $k \in \mathbb {N}_{\geq 2}, \xi \in (0,1]$
be fixed and let G be a
$k \in \mathbb {N}_{\geq 2}, \xi \in (0,1]$
be fixed and let G be a
![]() $\xi $
-expanding k-graph on n vertices with average vertex degreeFootnote
2
$\xi $
-expanding k-graph on n vertices with average vertex degreeFootnote
2
![]() $d=d(G)$
. For all
$d=d(G)$
. For all
![]() $j \in \mathbb {N}$
, the cop number of G satisfies the following.
$j \in \mathbb {N}$
, the cop number of G satisfies the following.
-
(1) If
 $n^{\frac {1}{2j+1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
, then with
$n^{\frac {1}{2j+1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
, then with
 ${\lambda } = \left \lceil \frac {n}{d^{2j+1}} \log n \right \rceil $
,
${\lambda } = \left \lceil \frac {n}{d^{2j+1}} \log n \right \rceil $
,  $$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-2} d^{j} {\lambda}. \end{align*} $$
$$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-2} d^{j} {\lambda}. \end{align*} $$
-
(2) If
 $\left (\frac {n}{k}\right )^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j}}$
, then
$\left (\frac {n}{k}\right )^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j}}$
, then  $$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-1} \frac{n}{k d^j } \log n. \end{align*} $$
$$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-1} \frac{n}{k d^j } \log n. \end{align*} $$
-
(3) If
 $n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}}$
, then with
$n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}}$
, then with
 ${\lambda } = \max _{} \left \{ \left \lceil \frac {n}{d^{2j}} \log n \right \rceil ,\left \lceil \frac {k}{d^{j}} \log n \right \rceil \right \}$
,
${\lambda } = \max _{} \left \{ \left \lceil \frac {n}{d^{2j}} \log n \right \rceil ,\left \lceil \frac {k}{d^{j}} \log n \right \rceil \right \}$
,  $$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-2} \frac{d^{j}}{k} {\lambda}. \end{align*} $$
$$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-2} \frac{d^{j}}{k} {\lambda}. \end{align*} $$
-
(4) If
 $(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
, then
$(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
, then  $$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-1} \frac{n}{d^{j}} \log n. \end{align*} $$
$$ \begin{align*} c\left(G\right) \leq 20 {\xi}^{-1} \frac{n}{d^{j}} \log n. \end{align*} $$
Let us explain in more detail the bounds in Theorem 1.6. In general, the upper bounds in Theorem 1.6 are increasing in d in the regimes (1) and (3) and decreasing in d in the regimes (2) and (4). In particular, and perhaps surprisingly, if we fix k and n and vary d, in certain regimes, increasing the average degree, and hence the number of edges, can help the cops, and in other regimes, increasing the number of edges can help the robber.
We note that some of the regimes of Theorem 1.6 can “collapse” if the left border of a regime is larger than its right border. Specifically, this can happen in regime (1), if we have
![]() $d \leq n^{\frac {1}{2j}}$
and
$d \leq n^{\frac {1}{2j}}$
and
![]() $n^{\frac {1}{2j+1}}> \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
or equivalently
$n^{\frac {1}{2j+1}}> \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
or equivalently
![]() $k> n^{\frac {1}{2j+1}}$
and it can happen in regime (4), if
$k> n^{\frac {1}{2j+1}}$
and it can happen in regime (4), if
![]() $d \leq n^{\frac {1}{2j-1}}$
and
$d \leq n^{\frac {1}{2j-1}}$
and
![]() $(nk)^{\frac {1}{2j}}> n^{\frac {1}{2j-1}}$
, or equivalently
$(nk)^{\frac {1}{2j}}> n^{\frac {1}{2j-1}}$
, or equivalently
![]() $k> n^{\frac {1}{2j-1}}$
. However, under the reasonable assumption that G is connected, we have
$k> n^{\frac {1}{2j-1}}$
. However, under the reasonable assumption that G is connected, we have
![]() $k \leq d$
, and so this second case does not occur, and the first case only occurs if
$k \leq d$
, and so this second case does not occur, and the first case only occurs if
![]() $n^{\frac {1}{2j+1}} \leq k \leq d \leq n^{\frac {1}{2j}}$
holds for some
$n^{\frac {1}{2j+1}} \leq k \leq d \leq n^{\frac {1}{2j}}$
holds for some
![]() $j \in \mathbb {N}$
. In this case, regime (1) collapses and the cop number is bounded as in (2). Furthermore, we note that the second argument of the maximum in the definition of
$j \in \mathbb {N}$
. In this case, regime (1) collapses and the cop number is bounded as in (2). Furthermore, we note that the second argument of the maximum in the definition of
![]() ${\lambda }$
in regime (3) is only relevant in the special case where
${\lambda }$
in regime (3) is only relevant in the special case where
![]() $k \geq \sqrt {n}$
. In that case, the factor takes its largest value of
$k \geq \sqrt {n}$
. In that case, the factor takes its largest value of
![]() $\log n$
for the smallest possible value of d, namely
$\log n$
for the smallest possible value of d, namely
![]() $d=k$
. For increasing d, the factor then decreases until d is larger than k by a
$d=k$
. For increasing d, the factor then decreases until d is larger than k by a
![]() $\log $
-factor, at which it attains its smallest value of
$\log $
-factor, at which it attains its smallest value of
![]() $1$
. Otherwise, in regimes (1) and (3), the factor
$1$
. Otherwise, in regimes (1) and (3), the factor
![]() ${\lambda }$
takes its largest value of
${\lambda }$
takes its largest value of
![]() $\log n$
at the left border of the respective regimes of d. Again, it then decreases with increasing d until it takes the value of
$\log n$
at the left border of the respective regimes of d. Again, it then decreases with increasing d until it takes the value of
![]() $1$
, which happens as soon as d is bound away from the left border by a sufficiently large multiplicative factor (
$1$
, which happens as soon as d is bound away from the left border by a sufficiently large multiplicative factor (
![]() $\log ^{\frac {1}{2j+1}} n$
in (1) and
$\log ^{\frac {1}{2j+1}} n$
in (1) and
![]() $\log ^{\frac {1}{2j}} n$
in (3)).
$\log ^{\frac {1}{2j}} n$
in (3)).
Our final result shows that whp
![]() $G^k(n,p)$
satisfies the desired expansion properties as long as k is growing with n and p is not too small.
$G^k(n,p)$
satisfies the desired expansion properties as long as k is growing with n and p is not too small.
Theorem 1.7 There exists a universal constant
![]() ${\xi }> 0$
such that if
${\xi }> 0$
such that if
![]() $k = k(n), p\,{=}\, p(n)\,{>}\,0$
are such that
$k = k(n), p\,{=}\, p(n)\,{>}\,0$
are such that
![]() $k = \omega (\log n)$
and
$k = \omega (\log n)$
and
![]() $\frac {n}{k} \geq p \binom {n-1}{k-1} = \omega \left (\log ^3 n\right )$
, then whp
$\frac {n}{k} \geq p \binom {n-1}{k-1} = \omega \left (\log ^3 n\right )$
, then whp
![]() $G^k(n,p)$
is
$G^k(n,p)$
is
![]() $\xi $
-expanding.
$\xi $
-expanding.
Let us give some intuition for the conditions on k and p. The value
![]() $p \binom {n-1}{k-1}$
is roughly the expected number of edges every vertex in
$p \binom {n-1}{k-1}$
is roughly the expected number of edges every vertex in
![]() $G^k(n,p)$
meets, and the lower bound on this quantity ensures that we can assume this is concentrated around its expectation. On the other hand,
$G^k(n,p)$
meets, and the lower bound on this quantity ensures that we can assume this is concentrated around its expectation. On the other hand,
![]() $p k \binom {n-1}{k-1}$
is roughly the expected degree of a vertex in
$p k \binom {n-1}{k-1}$
is roughly the expected degree of a vertex in
![]() $G^k(n,p)$
, and so it is natural to restrict this to be at most n.
$G^k(n,p)$
, and so it is natural to restrict this to be at most n.
Note that it follows from Theorems 1.5 and 1.7 that Conjecture 1.8 holds for the same range of
![]() $n,p$
, and k up to polylogarithmic factors.
$n,p$
, and k up to polylogarithmic factors.
Corollary 1.8 If
![]() $k = k(n), p= p(n)>0$
are such that
$k = k(n), p= p(n)>0$
are such that
![]() $k = \omega (\log n)$
and
$k = \omega (\log n)$
and
![]() $\frac {n}{k} \geq p \binom {n-1}{k-1} = \omega (\log ^3 n)$
, then whp
$\frac {n}{k} \geq p \binom {n-1}{k-1} = \omega (\log ^3 n)$
, then whp
![]() $c\left (G^k(n,p)\right ) = \tilde {O}\left ( \sqrt {\frac {n}{k}}\,\right )$
.
$c\left (G^k(n,p)\right ) = \tilde {O}\left ( \sqrt {\frac {n}{k}}\,\right )$
.
Furthermore, Theorem 1.7 allows us to apply Theorem 1.6 to
![]() $G^k(n,p)$
for a broad range of parameters and we can bound
$G^k(n,p)$
for a broad range of parameters and we can bound
![]() $c\left (G^k(n,p)\right )$
more precisely in certain ranges. It turns out that a sensible parameterization to take is as follows. Let us define
$c\left (G^k(n,p)\right )$
more precisely in certain ranges. It turns out that a sensible parameterization to take is as follows. Let us define ![]() , which is roughly the expected degree of a vertex in
, which is roughly the expected degree of a vertex in
![]() $G^k(n,p)$
and let
$G^k(n,p)$
and let
![]() $\hat {d} = n^\alpha $
and
$\hat {d} = n^\alpha $
and
![]() $ k = n^\beta $
for some
$ k = n^\beta $
for some
![]() $0 < \beta \leq \alpha \leq 1$
. We consider the function
$0 < \beta \leq \alpha \leq 1$
. We consider the function
![]() $f_\beta \colon (\beta ,1) \to \mathbb {R}$
defined as
$f_\beta \colon (\beta ,1) \to \mathbb {R}$
defined as

with
![]() $\bar {c}$
being the upper bound for the cop number obtained from Theorem 1.6. It follows that
$\bar {c}$
being the upper bound for the cop number obtained from Theorem 1.6. It follows that
![]() $f_\beta $
again has a characteristic zigzag shape (see Figure 3). In contrast to the case of
$f_\beta $
again has a characteristic zigzag shape (see Figure 3). In contrast to the case of
![]() $G(n,p)$
(see Figure 1), the zigzag shape in
$G(n,p)$
(see Figure 1), the zigzag shape in
![]() $G^k(n,p)$
arises as the intersection of two complementary zigzags, coming from two different strategies, and so has twice as many peaks and troughs. In particular, it can be seen that
$G^k(n,p)$
arises as the intersection of two complementary zigzags, coming from two different strategies, and so has twice as many peaks and troughs. In particular, it can be seen that
![]() $f_\beta (\alpha ) \leq (1+o(1))\frac {1-\beta }{2}$
for all
$f_\beta (\alpha ) \leq (1+o(1))\frac {1-\beta }{2}$
for all
![]() $\alpha \in (\beta ,1)$
, corresponding to the bound of
$\alpha \in (\beta ,1)$
, corresponding to the bound of
![]() $\tilde {O}\left (\sqrt {\frac {n}{k}}\,\right )$
on the cop number.
$\tilde {O}\left (\sqrt {\frac {n}{k}}\,\right )$
on the cop number.

Figure 3: Alternating zigzag shape of the function
![]() $f_\beta (\alpha )$
for
$f_\beta (\alpha )$
for
![]() $\beta = \frac {2}{19}$
. The blue (dashed) line is the upper bound coming from the edge strategy, the red (dotted) line is the upper bound coming from the vertex strategy. As can be seen, the two strategies give rise to two alternating zigzag shapes, that together make up the single zigzag with increased frequency. We note that the worst bounds occur at the intersection points of the two lines, which all lie on the green (solid) line at
$\beta = \frac {2}{19}$
. The blue (dashed) line is the upper bound coming from the edge strategy, the red (dotted) line is the upper bound coming from the vertex strategy. As can be seen, the two strategies give rise to two alternating zigzag shapes, that together make up the single zigzag with increased frequency. We note that the worst bounds occur at the intersection points of the two lines, which all lie on the green (solid) line at
![]() $\frac {1-\beta }{2}$
.
$\frac {1-\beta }{2}$
.
1.3 Techniques
To give a lower bound for the cop number, we need to exhibit a strategy for the cops. As in the work of Łuczak and Prałat [Reference Łuczak and Prałat21], we show the existence of a strategy for the cops to surround the robber using a probabilistic argument. While in [Reference Łuczak and Prałat21] the strategies focused solely on surrounding a small vertex-neighborhood of the robber, we also consider a second type of strategy which aims to surround a small edge-neighborhood, and utilize both these strategies in our result.
Assuming the robber starts on a vertex v, after his first r moves, the robber has to be in the rth vertex-neighborhood ![]() , and specifically in some edge of the rth edge-neighborhood
, and specifically in some edge of the rth edge-neighborhood ![]() . The cops aim to occupy each edge in
. The cops aim to occupy each edge in ![]() before the robber has had time to leave this set. Since the cops move first and a cop can catch the robber in a single move once they occupy the same edge, the cops need to occupy each edge in
before the robber has had time to leave this set. Since the cops move first and a cop can catch the robber in a single move once they occupy the same edge, the cops need to occupy each edge in ![]() within their first r moves (see Figure 4). The strategy of surrounding via vertices works similarly, the only difference being that the cops surround the rth vertex-neighborhood and have
within their first r moves (see Figure 4). The strategy of surrounding via vertices works similarly, the only difference being that the cops surround the rth vertex-neighborhood and have
![]() $r+1$
moves before the robber can escape. The payoff in choosing to surround via vertices or edges can be seen as follows – in the former, we can use cops at a larger distance, and so in general we will have more cops to work with, whereas in the latter, since each edge contains many vertices, we will not have to occupy as many edges as we would have vertices, and so perhaps we can catch the robber with fewer cops.
$r+1$
moves before the robber can escape. The payoff in choosing to surround via vertices or edges can be seen as follows – in the former, we can use cops at a larger distance, and so in general we will have more cops to work with, whereas in the latter, since each edge contains many vertices, we will not have to occupy as many edges as we would have vertices, and so perhaps we can catch the robber with fewer cops.

Figure 4: A visualization of the edge-surrounding strategy. The cops try to cover all edges of the third edge-neighborhood of v in three moves, which is possible if there is a matching between ![]() and all vertices occupied by cops within distance three of these edges, which covers all edges of
and all vertices occupied by cops within distance three of these edges, which covers all edges of ![]() .
.
For a fixed vertex v and a fixed distance r, the existence of such a strategy can then be reduced to a matching problem – for instance, in the case of the edge strategy, for each edge e at distance at most r from v, we need to assign a unique cop at distance at most r from e, whose strategy is to occupy e within the first r turns of the game. We aim to show (see Claims 1 and 2) that such an assignment of cops can be found with positive probability if we choose a random set of cops, assigning a cop to each vertex in the graph independently with some probability q (see Figure 4).
Assuming that our k-graph G is
![]() $\xi $
-expanding, we have quite good control over the sizes of
$\xi $
-expanding, we have quite good control over the sizes of ![]() and
and ![]() , and also over the number of vertices at a fixed distance from each vertex and edge contained in these sets. Using some standard probabilistic and combinatorial tools, we can show that for an appropriate choice of q, with positive probability, we can find an appropriate assignment of cops for each possible starting vertex v and bound the number of cops m we use in such a strategy, which in general depends not only on r but also on the uniformity k and average degree d of G.
, and also over the number of vertices at a fixed distance from each vertex and edge contained in these sets. Using some standard probabilistic and combinatorial tools, we can show that for an appropriate choice of q, with positive probability, we can find an appropriate assignment of cops for each possible starting vertex v and bound the number of cops m we use in such a strategy, which in general depends not only on r but also on the uniformity k and average degree d of G.
This leads to a family of bounds on the cop number, one for each
![]() $r\in \mathbb {N}$
, for both the vertex and edge surrounding strategy. For a fixed choice of parameters k and d, we then have to solve an integer optimization problem to find which choice of r (and of a vertex or edge surrounding strategy) leads to the best bound on the cop number, from which we can derive the bounds in Theorem 1.6.
$r\in \mathbb {N}$
, for both the vertex and edge surrounding strategy. For a fixed choice of parameters k and d, we then have to solve an integer optimization problem to find which choice of r (and of a vertex or edge surrounding strategy) leads to the best bound on the cop number, from which we can derive the bounds in Theorem 1.6.
1.4 Outline of the paper
The rest of the paper is structured as follows. In Section 2, we introduce some notation and important definitions and state some auxiliary results. In Section 3, we prove Theorems 1.5 and 1.6, and in Section 4, we prove Theorem 1.7. We conclude in Section 5 by discussing some unresolved questions and possible directions for future research.
2 Preliminaries
All asymptotics in the paper are taken as n tends to infinity. We say that a statement
![]() $A(n)$
holds with high probability (whp for short) if
$A(n)$
holds with high probability (whp for short) if
![]() $\lim _{n \to \infty } \mathbb {P}\left [A(n)\right ] = 1$
. We use standard Landau notation for all asymptotics. Furthermore, we omit floors or ceilings in proofs to improve readability. Let
$\lim _{n \to \infty } \mathbb {P}\left [A(n)\right ] = 1$
. We use standard Landau notation for all asymptotics. Furthermore, we omit floors or ceilings in proofs to improve readability. Let
![]() $\mathbb {N}_0 = \mathbb {N} \cup \{0\}$
and
$\mathbb {N}_0 = \mathbb {N} \cup \{0\}$
and
![]() $\mathbb {N}_{\geq 2} = \{2,3,\ldots \}$
. Throughout the paper, we assume
$\mathbb {N}_{\geq 2} = \{2,3,\ldots \}$
. Throughout the paper, we assume
![]() $k \in \mathbb {N}_{\geq 2}$
.
$k \in \mathbb {N}_{\geq 2}$
.
Let G be a k-uniform hypergraph, or k-graph, on vertex set
![]() $[n]$
. The distance between two different vertices
$[n]$
. The distance between two different vertices
![]() $d_G (x,y ) $
is equal to the smallest length of a loose path between them, that is, the smallest
$d_G (x,y ) $
is equal to the smallest length of a loose path between them, that is, the smallest
![]() $t \in \mathbb {N}$
such that there exists a sequence
$t \in \mathbb {N}$
such that there exists a sequence
![]() $e_1,e_2,\ldots , e_t$
of edges such that
$e_1,e_2,\ldots , e_t$
of edges such that
![]() $x \in e_1, y \in e_t$
and
$x \in e_1, y \in e_t$
and
![]() $e_i \cap e_{i+1} \neq \emptyset $
for all
$e_i \cap e_{i+1} \neq \emptyset $
for all
![]() $1\leq i \leq t-1$
. Furthermore, we define
$1\leq i \leq t-1$
. Furthermore, we define
![]() $d_G (x,x ) = 0$
, for all
$d_G (x,x ) = 0$
, for all
![]() $x \in V(G)$
. The distance between two sets of vertices A and
$x \in V(G)$
. The distance between two sets of vertices A and
![]() $A'$
is defined as the minimum distance between all pairs of vertices from the two sets:
$A'$
is defined as the minimum distance between all pairs of vertices from the two sets:
For a set of vertices
![]() $A \subseteq V(G)$
and
$A \subseteq V(G)$
and
![]() $r \in \mathbb {N}_0$
, we denote the closed rth vertex-neighborhood of A by
$r \in \mathbb {N}_0$
, we denote the closed rth vertex-neighborhood of A by ![]() . Formally,
. Formally,
For a set of edges
![]() $B \subseteq E(G)$
, we write
$B \subseteq E(G)$
, we write
for the set of all vertices contained in at least one of the edges in B. We extend the definition of the closed rth vertex-neighborhood to sets of edges in the obvious way by setting
Furthermore, for a set of vertices
![]() $A \subseteq V(G)$
and
$A \subseteq V(G)$
and
![]() $r \in \mathbb {N}$
, we define the closed rth edge-neighborhood of A as
$r \in \mathbb {N}$
, we define the closed rth edge-neighborhood of A as
Note that to be included in the rth edge-neighborhood, an edge has to be within distance
![]() $r-1$
of the respective vertex set. The motivation behind this parameter shift is that the amount of “discovered” vertices is the same for the rth vertex- and edge-neighborhood, or in other words
$r-1$
of the respective vertex set. The motivation behind this parameter shift is that the amount of “discovered” vertices is the same for the rth vertex- and edge-neighborhood, or in other words ![]() . For notational convenience, we will omit the superscript for the first vertex- and edge-neighborhood and write
. For notational convenience, we will omit the superscript for the first vertex- and edge-neighborhood and write ![]() and
and ![]() , respectively.
, respectively.
We denote the average vertex degree of G by
where we consider the degree of a vertex v to be
![]() $|N_V(v)|$
, and not
$|N_V(v)|$
, and not
![]() $|N_E(v)|$
which is also sometimes referred to as the degree of a vertex in a hypergraph.
$|N_E(v)|$
which is also sometimes referred to as the degree of a vertex in a hypergraph.
Note that the average vertex degree of
![]() $G^k(n,p)$
, i.e.,
$G^k(n,p)$
, i.e., ![]() , is a random variable that is concentrated around its expectation, which is given as
, is a random variable that is concentrated around its expectation, which is given as
For appropriate ranges of p and k, we can estimate
![]() $\mathbb {E}\left [d\right ]$
as follows:
$\mathbb {E}\left [d\right ]$
as follows:
where the penultimate equation holds when
![]() $p\binom {n-2}{k-2} = o(1)$
and the final equation holds for
$p\binom {n-2}{k-2} = o(1)$
and the final equation holds for
![]() $k = o(n)$
. In the context of Cops and Robber games on random hypergraphs, these are reasonable assumptions, as otherwise either each edge-neighborhood (deterministically) or each vertex-neighborhood (in expectation) covers a constant fraction of the vertex set. If the graph is also connected, it can be shown in both cases that the cop number is then whp at most logarithmic in n. We will also restrict ourselves to the case
$k = o(n)$
. In the context of Cops and Robber games on random hypergraphs, these are reasonable assumptions, as otherwise either each edge-neighborhood (deterministically) or each vertex-neighborhood (in expectation) covers a constant fraction of the vertex set. If the graph is also connected, it can be shown in both cases that the cop number is then whp at most logarithmic in n. We will also restrict ourselves to the case
![]() $d\geq k \geq 2$
, since for
$d\geq k \geq 2$
, since for
![]() $d <k$
the hypergraph will contain isolated vertices. Since the cop number is additive over disjoint unions, it is natural to restrict our attention to connected hypergraphs.
$d <k$
the hypergraph will contain isolated vertices. Since the cop number is additive over disjoint unions, it is natural to restrict our attention to connected hypergraphs.
For convenience, rather than working with d, we will work with the following explicit quantity:
We will show later (see Lemma 4.3) that the size of the first vertex-neighborhood of every vertex in
![]() $G^k(n,p)$
lies close to
$G^k(n,p)$
lies close to
![]() $\hat {d}$
, from which it then follows, that d is approximately
$\hat {d}$
, from which it then follows, that d is approximately
![]() $\hat {d}$
.
$\hat {d}$
.
Definition 2.1 Let G be a k-graph on n vertices with average vertex degree
![]() $d\geq k$
. Given a positive constant
$d\geq k$
. Given a positive constant
![]() $0< {\xi } \leq 1$
, which we call the expanding constant, we say G is
$0< {\xi } \leq 1$
, which we call the expanding constant, we say G is
![]() $\xi $
-expanding if G has the following properties.
$\xi $
-expanding if G has the following properties.
-
(A.1) For every vertex
 $v \in V(G)$
and
$v \in V(G)$
and
 $r \in \mathbb {N}$
satisfying
$r \in \mathbb {N}$
satisfying
 $d^r \leq \sqrt {nk}$
,
$d^r \leq \sqrt {nk}$
, 
-
(A.2) For every subset
 $A \subseteq V(G)$
of vertices and
$A \subseteq V(G)$
of vertices and
 $r \in \mathbb {N}$
,
$r \in \mathbb {N}$
, 
-
(A.3) For every subset
 $B \subseteq E(G)$
of edges and
$B \subseteq E(G)$
of edges and
 $r \in \mathbb {N}$
,
$r \in \mathbb {N}$
, 
Throughout the paper, we use the following corollaries of the Chernoff bounds (see, for example, [Reference Janson, Łuczak and Rucinski18, Theorem 2.1 and Corollary 2.3]).
Theorem 2.1 Let
![]() $X \sim \textrm {Bin}(n,p)$
. Then, for any
$X \sim \textrm {Bin}(n,p)$
. Then, for any
![]() $t>0$
, we have
$t>0$
, we have
 $$ \begin{align} \mathbb{P}\left[\,|X - \mathbb{E}\left[X\right]| \geq t\,\right] \leq 2 \exp \left( -\frac{t^2}{2\left(\mathbb{E}\left[X\right]+t/3\right)}\right) \end{align} $$
$$ \begin{align} \mathbb{P}\left[\,|X - \mathbb{E}\left[X\right]| \geq t\,\right] \leq 2 \exp \left( -\frac{t^2}{2\left(\mathbb{E}\left[X\right]+t/3\right)}\right) \end{align} $$
and
 $$ \begin{align} \mathbb{P}\left[\,X \leq \mathbb{E}\left[X\right] - t\,\right] \leq \exp \left(-\frac{t^2}{2 \mathbb{E}\left[X\right]} \right). \end{align} $$
$$ \begin{align} \mathbb{P}\left[\,X \leq \mathbb{E}\left[X\right] - t\,\right] \leq \exp \left(-\frac{t^2}{2 \mathbb{E}\left[X\right]} \right). \end{align} $$
In particular, if
![]() $a \leq 10 \mathbb {E}\left [X\right ]$
, then
$a \leq 10 \mathbb {E}\left [X\right ]$
, then
An important step in the proof of the main theorems is constructing matchings in specific bipartite graphs which cover one partition class. To this end, we use Hall’s marriage theorem, which we state here for the sake of completeness.
Theorem 2.2 [Reference Hall16, Theorem 1], Theorem 1
Let
![]() $(A\cup B,E)$
be a bipartite graph. The following two statements are equivalent.
$(A\cup B,E)$
be a bipartite graph. The following two statements are equivalent.
-
(1) There is a matching covering all vertices of A.
-
(2)
 $ |N_V(X)\setminus X |\geq |X|$
for all
$ |N_V(X)\setminus X |\geq |X|$
for all
 $X \subseteq A$
.
$X \subseteq A$
.
3 Proofs of Theorems 1.5 and 1.6
We start by proving Theorem 1.6, from which Theorem 1.5 follows as a direct consequence.
Proof Let G be a
![]() $\xi $
-expanding k-graph on n vertices. Note that, as the stated bounds on the cop number are all clearly at least
$\xi $
-expanding k-graph on n vertices. Note that, as the stated bounds on the cop number are all clearly at least
![]() $20$
, we can assume w.l.o.g. that
$20$
, we can assume w.l.o.g. that
![]() $n\geq 20$
.
$n\geq 20$
.
Our strategy is to choose the initial placement of our cops in such a way that we can catch the robber in j moves for some
![]() $j \in \mathbb {N}$
. In order to show the existence of such a choice of initial positions, we will use the expansion properties of G to show that a random choice succeeds with positive probability.
$j \in \mathbb {N}$
. In order to show the existence of such a choice of initial positions, we will use the expansion properties of G to show that a random choice succeeds with positive probability.
In regimes (1) and (4), we will catch the robber by surrounding its
![]() $(j-1)$
st vertex-neighborhood. In fact, cops that start too far from the robber will not actively participate in the game. The following key claim characterizes how many cops we need in the respective regimes to guarantee that sufficiently many cops are close enough to the starting vertex of the robber to make this strategy work. The proof of the claim is deferred to the end of this section.
$(j-1)$
st vertex-neighborhood. In fact, cops that start too far from the robber will not actively participate in the game. The following key claim characterizes how many cops we need in the respective regimes to guarantee that sufficiently many cops are close enough to the starting vertex of the robber to make this strategy work. The proof of the claim is deferred to the end of this section.
Claim 1 Let
![]() $j \in \mathbb {N}$
. There exists a subset
$j \in \mathbb {N}$
. There exists a subset
![]() $Y \subseteq V(G)$
such that for every vertex
$Y \subseteq V(G)$
such that for every vertex
![]() $v \in V(G)$
, there exists an injection
$v \in V(G)$
, there exists an injection ![]() such that for every vertex
such that for every vertex ![]() , we have
, we have
![]() $d_G (x,f(x) ) \leq j$
. Furthermore,
$d_G (x,f(x) ) \leq j$
. Furthermore,
-
(a) if
 $j \neq 1$
and
$j \neq 1$
and
 $n^{\frac {1}{2j-1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j-2}}$
, then
$n^{\frac {1}{2j-1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j-2}}$
, then
 $|Y| \leq 20 {\xi }^{-2}d^{j-1} \left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil $
;
$|Y| \leq 20 {\xi }^{-2}d^{j-1} \left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil $
; -
(d) if
 $(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
, then
$(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
, then
 $|Y| \leq 20 {\xi }^{-1}\frac {n}{d^j} \log n$
.
$|Y| \leq 20 {\xi }^{-1}\frac {n}{d^j} \log n$
.
Given Y as in the claim, the cops’ strategy is to initially occupy the vertices of Y. The robber starts on some vertex v. By Claim 1, there exists an injection f such that for every vertex ![]() , the cop on vertex
, the cop on vertex
![]() $f(x)$
is within distance j of x at the start of the game. Each cop which starts on a vertex w in the image
$f(x)$
is within distance j of x at the start of the game. Each cop which starts on a vertex w in the image ![]() moves to the vertex
moves to the vertex
![]() $f^{-1}(w)$
in the first j moves. After
$f^{-1}(w)$
in the first j moves. After
![]() $j-1$
moves, the robber is positioned at some vertex
$j-1$
moves, the robber is positioned at some vertex ![]() . Since the cops move first, in the next turn, the cop that started on the vertex
. Since the cops move first, in the next turn, the cop that started on the vertex
![]() $f(w)$
moves to the vertex w and catches the robber. Note that in regime (1), we use the described strategy after applying the index shift
$f(w)$
moves to the vertex w and catches the robber. Note that in regime (1), we use the described strategy after applying the index shift
![]() $j \to j+1$
to obtain the desired result.
$j \to j+1$
to obtain the desired result.
In regimes (2) and (3), we instead catch the robber by surrounding his jth edge-neighborhood. Similar to the previous case, it suffices to prove the following claim, which we will do at the end of this section.
Claim 2 Let
![]() $j \in \mathbb {N}$
. There exists a subset
$j \in \mathbb {N}$
. There exists a subset
![]() $Z \subseteq V(G)$
such that for all vertices
$Z \subseteq V(G)$
such that for all vertices
![]() $v \in V(G)$
there exists an injection
$v \in V(G)$
there exists an injection ![]() , such that for every edge
, such that for every edge ![]() , we have
, we have
![]() $d_G (e,g(e) ) \leq j$
. Furthermore,
$d_G (e,g(e) ) \leq j$
. Furthermore,
-
(b) if
 $\left (\frac {n}{k}\right )^{\frac {1}{2j}}\leq d \leq n^{\frac {1}{2j}}$
, then
$\left (\frac {n}{k}\right )^{\frac {1}{2j}}\leq d \leq n^{\frac {1}{2j}}$
, then
 $|Z| \leq 20 {\xi }^{-1} \frac {n}{kd^j} \log n$
;
$|Z| \leq 20 {\xi }^{-1} \frac {n}{kd^j} \log n$
; -
(c) if
 $n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}} $
, then
$n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}} $
, then
 $|Z| \leq 20 {\xi }^{-2}\frac {d^j}{k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {k}{d^{j}} \log n \right \rceil $
.
$|Z| \leq 20 {\xi }^{-2}\frac {d^j}{k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {k}{d^{j}} \log n \right \rceil $
.
Indeed, given such a set Z, the cops’ strategy is to initially occupy the vertices of Z. The robber starts on some vertex v. By Claim 2, there exists an injection g such that for every edge ![]() , we have
, we have
![]() $d_G (e,g(e) ) \leq j$
. Each cop which starts on a vertex w in the image
$d_G (e,g(e) ) \leq j$
. Each cop which starts on a vertex w in the image ![]() moves to some vertex u in the edge
moves to some vertex u in the edge
![]() $g^{-1}(w)$
in the first j moves. After j moves, the robber is on some vertex x in some edge
$g^{-1}(w)$
in the first j moves. After j moves, the robber is on some vertex x in some edge ![]() . Since the cops move first, the cop that started at
. Since the cops move first, the cop that started at
![]() $g(e)$
is currently at some vertex
$g(e)$
is currently at some vertex
![]() $u \in e$
, and hence can catch the robber in the next move.
$u \in e$
, and hence can catch the robber in the next move.
It remains to prove the two claims.
Proof of Claim 1
Clearly, such a set Y exists if we do not make any restrictions on its size, so we may assume that one of (a) or (d) holds. We will choose our set Y by specifying some probability q and letting each vertex lie in Y independently with probability q. We show that with positive probability a random choice of Y satisfies the conclusions of the claim, and hence there must exist some suitable set Y.
Let us start with case (d), so we are assuming that
![]() $(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
. In this case, we set
$(nk)^{\frac {1}{2j}} \leq d \leq n^{\frac {1}{2j-1}}$
. In this case, we set
![]() $q = 10 {\xi }^{-1} d^{-j} \log n$
, where we note that our assumptions on d ensure that
$q = 10 {\xi }^{-1} d^{-j} \log n$
, where we note that our assumptions on d ensure that
![]() $q \leq 1$
. Since
$q \leq 1$
. Since
![]() $|Y| \sim \text {Bin}(n,q)$
, it follows from the Chernoff bound (2.4) that
$|Y| \sim \text {Bin}(n,q)$
, it follows from the Chernoff bound (2.4) that
![]() $|Y| \leq 20 \frac {n}{{\xi } d^{j}} \log n$
with probability at least
$|Y| \leq 20 \frac {n}{{\xi } d^{j}} \log n$
with probability at least
![]() $\frac {2}{3}$
. We will show that an injection as stated in the claim exists with probability at least
$\frac {2}{3}$
. We will show that an injection as stated in the claim exists with probability at least
![]() $\frac {2}{3}$
, and hence Y satisfies the conclusion of the claim with probability at least
$\frac {2}{3}$
, and hence Y satisfies the conclusion of the claim with probability at least
![]() $\frac {1}{3}>0$
.
$\frac {1}{3}>0$
.
Given a fixed vertex
![]() $v \in V$
, an injection of the desired form corresponds to a matching in the bipartite graph
$v \in V$
, an injection of the desired form corresponds to a matching in the bipartite graph ![]() with edge set
with edge set ![]() , which covers all vertices of
, which covers all vertices of ![]() . To find a matching as described above, it is enough to check that Hall’s condition (see Theorem 2.2) is satisfied for all
. To find a matching as described above, it is enough to check that Hall’s condition (see Theorem 2.2) is satisfied for all ![]() .
.
We split into two cases. First, suppose that ![]() with
with
![]() $a:=|A| \leq \frac {n}{d^j}$
. Slightly abusing notation, we write
$a:=|A| \leq \frac {n}{d^j}$
. Slightly abusing notation, we write
![]() $N_H(A)$
for the vertices at exactly distance
$N_H(A)$
for the vertices at exactly distance
![]() $1$
from A in the auxiliary graph H. By Property (A.2), it follows that
$1$
from A in the auxiliary graph H. By Property (A.2), it follows that ![]() . Thus, by our choice of Y, we have
. Thus, by our choice of Y, we have ![]() stochastically dominates a binomial random variable
stochastically dominates a binomial random variable
![]() $\textrm {Bin} \left ({\xi } ad^{j},q \right )$
, the expectation of which satisfies
$\textrm {Bin} \left ({\xi } ad^{j},q \right )$
, the expectation of which satisfies
![]() $\mathbb {E}\left [\textrm {Bin} \left ( {\xi } ad^{j},q \right )\right ]= {\xi } ad^{j }q \geq 10 a \log n $
. Therefore, by the Chernoff bound (2.6), it follows that
$\mathbb {E}\left [\textrm {Bin} \left ( {\xi } ad^{j},q \right )\right ]= {\xi } ad^{j }q \geq 10 a \log n $
. Therefore, by the Chernoff bound (2.6), it follows that
 $$\begin{align*}&\mathbb{P}\left[\,|N_H(A)|< |A|\,\right] \leq \mathbb{P}\left[\textrm{Bin}\left({\xi} ad^{j},q\right) < a\right] \\&\quad\leq \mathbb{P}\left[\textrm{Bin}\left({\xi} ad^{j},q\right) \leq a \log n\right] \leq \exp(-4 a \log n) = n^{-4a}. \end{align*}$$
$$\begin{align*}&\mathbb{P}\left[\,|N_H(A)|< |A|\,\right] \leq \mathbb{P}\left[\textrm{Bin}\left({\xi} ad^{j},q\right) < a\right] \\&\quad\leq \mathbb{P}\left[\textrm{Bin}\left({\xi} ad^{j},q\right) \leq a \log n\right] \leq \exp(-4 a \log n) = n^{-4a}. \end{align*}$$
Then, using a union bound over all sets ![]() with
with
![]() $|A| \leq \frac {n}{d^j}$
, we can bound the probability that there exists such a set A that violates Hall’s condition from above by
$|A| \leq \frac {n}{d^j}$
, we can bound the probability that there exists such a set A that violates Hall’s condition from above by

In the second case, when
![]() $a:=|A|> \frac {n}{d^j}$
, we note that since
$a:=|A|> \frac {n}{d^j}$
, we note that since ![]() , by Property (A.2), we have
, by Property (A.2), we have ![]() and
and ![]() . Hence,
. Hence, ![]() stochastically dominates a binomial random variable
stochastically dominates a binomial random variable
![]() $\textrm {Bin} \left ({\xi } n,q \right )$
, the expectation of which satisfies
$\textrm {Bin} \left ({\xi } n,q \right )$
, the expectation of which satisfies
Here, we used the fact that in this regime we have
![]() $d \leq n^{\frac {1}{2j-1}}$
. From the Chernoff bound (2.6), it follows that
$d \leq n^{\frac {1}{2j-1}}$
. From the Chernoff bound (2.6), it follows that
 $$\begin{align*}&\mathbb{P}\left[\,|N_H(A)|< |A|\,\right] \leq \mathbb{P}\left[\textrm{Bin} \left( {\xi} n,q \right) <a \right] \\&\quad\leq \mathbb{P}\left[\textrm{Bin} \left({\xi} n,q \right) \leq {\xi}^{-1} d^{j-1} \log n\right] \leq \exp(-4 d^{j-1} \log n) = n^{-4d^{j-1}}. \end{align*}$$
$$\begin{align*}&\mathbb{P}\left[\,|N_H(A)|< |A|\,\right] \leq \mathbb{P}\left[\textrm{Bin} \left( {\xi} n,q \right) <a \right] \\&\quad\leq \mathbb{P}\left[\textrm{Bin} \left({\xi} n,q \right) \leq {\xi}^{-1} d^{j-1} \log n\right] \leq \exp(-4 d^{j-1} \log n) = n^{-4d^{j-1}}. \end{align*}$$
Again, using the union bound and the fact that
![]() $a \leq {\xi }^{-1} d^{j-1}$
, we can bound the probability that there is such a set A violating Hall’s condition from above by
$a \leq {\xi }^{-1} d^{j-1}$
, we can bound the probability that there is such a set A violating Hall’s condition from above by

Thus, for every vertex v, an injection of the desired form exists with probability at least
![]() $1-\frac {1}{3n}$
. Using another union bound over all vertices, we can bound the probability that there exists a vertex for which there is no such injection by
$1-\frac {1}{3n}$
. Using another union bound over all vertices, we can bound the probability that there exists a vertex for which there is no such injection by
![]() $\frac {1}{3}$
, concluding the proof in the case (d).
$\frac {1}{3}$
, concluding the proof in the case (d).
In the case (a), where
![]() $n^{\frac {1}{2j-1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j-2}}$
, we proceed similarly as in case (d), but with a slightly different value of q. We let
$n^{\frac {1}{2j-1}} \leq d \leq \left (\frac {n}{k}\right )^{\frac {1}{2j-2}}$
, we proceed similarly as in case (d), but with a slightly different value of q. We let
![]() $q = 10 {\xi }^{-2} \frac {d^{j-1}}{n} \left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil $
, noting again that our assumptions on d ensure that
$q = 10 {\xi }^{-2} \frac {d^{j-1}}{n} \left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil $
, noting again that our assumptions on d ensure that
![]() $q \leq 1$
.
$q \leq 1$
.
Arguing as before, splitting into cases according to whether or not
![]() $|A|> \frac {n}{d^j}$
, we see that it suffices to prove the following two inequalities:
$|A|> \frac {n}{d^j}$
, we see that it suffices to prove the following two inequalities:

and

To show (3.3), we note that
Then, as before, it is clear that (2.6) yields the desired concentration to bound the sum as in (3.1).
Similarly, to show (3.4), we first note that, since
![]() $\left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil \geq 1$
, it follows that
$\left \lceil \frac {n}{d^{2j-1}} \log n \right \rceil \geq 1$
, it follows that
![]() $\mathbb {E}\left [\textrm {Bin} \left ({\xi } n,q \right )\right ] = {\xi } n q \geq 10 {\xi }^{-1} d^{j-1}$
. Hence, by (2.6),
$\mathbb {E}\left [\textrm {Bin} \left ({\xi } n,q \right )\right ] = {\xi } n q \geq 10 {\xi }^{-1} d^{j-1}$
. Hence, by (2.6),
and since
![]() $a \leq {\xi }^{-1}d^{j-1}$
by Property (A.2), we can bound the sum as in (3.2), although we have to be more careful in our estimates. Plugging into (3.4), we obtain
$a \leq {\xi }^{-1}d^{j-1}$
by Property (A.2), we can bound the sum as in (3.2), although we have to be more careful in our estimates. Plugging into (3.4), we obtain

where we used the facts that
![]() $d^{j-1} \geq n^{\frac {j-1}{2j-1}} \geq n^{\frac {1}{3}}$
, as
$d^{j-1} \geq n^{\frac {j-1}{2j-1}} \geq n^{\frac {1}{3}}$
, as
![]() $j \geq 2$
, and that
$j \geq 2$
, and that
![]() $n \geq 20$
.
$n \geq 20$
.
Proof of Claim 2
As in the previous claim, the existence of such a set Y is clear if we make no assumptions on its size, so we may assume that one of (b) or (c) holds. Again, we will choose the set Y by letting each vertex lie in Y independently with some fixed probability q and show that with positive probability such a set Y satisfies the conclusions of the claim.
Let us start with case (c), where
![]() $n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}}$
. Here, we set
$n^{\frac {1}{2j}} \leq d \leq (nk)^{\frac {1}{2j}}$
. Here, we set
![]() $q=10{\xi }^{-2} \frac {d^{j}}{ n k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
. As in the previous claim, it follows from (2.4) that
$q=10{\xi }^{-2} \frac {d^{j}}{ n k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
. As in the previous claim, it follows from (2.4) that
![]() $|Y| \leq 20 \frac {d^{j}}{{\xi }^{2}k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
with probability at least
$|Y| \leq 20 \frac {d^{j}}{{\xi }^{2}k} \left \lceil \frac {n}{d^{2j}} \log n \right \rceil \left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
with probability at least
![]() $\frac {2}{3}$
. We will show that an injection as stated in the claim exists with probability at least
$\frac {2}{3}$
. We will show that an injection as stated in the claim exists with probability at least
![]() $\frac {2}{3}$
, and hence Y satisfies the conclusion of the claim with probability at least
$\frac {2}{3}$
, and hence Y satisfies the conclusion of the claim with probability at least
![]() $\frac {1}{3}>0$
.
$\frac {1}{3}>0$
.
Given a fixed
![]() $v \in V$
, an injection of the desired form corresponds to a matching in the bipartite graph
$v \in V$
, an injection of the desired form corresponds to a matching in the bipartite graph ![]() with
with ![]() , which covers all of
, which covers all of ![]() . To find such a matching, it is enough to check that Hall’s condition (see Theorem 2.2) is satisfied for all
. To find such a matching, it is enough to check that Hall’s condition (see Theorem 2.2) is satisfied for all ![]() . We again split into two cases, depending on the size of B.
. We again split into two cases, depending on the size of B.
First, suppose that
![]() $b:=|B| \leq \frac {n}{kd^j}$
. Then, by Property (A.3), it follows that
$b:=|B| \leq \frac {n}{kd^j}$
. Then, by Property (A.3), it follows that ![]() and so
and so ![]() stochastically dominates a binomial random variable
stochastically dominates a binomial random variable
![]() $\textrm {Bin} \left ({\xi } b k d^{j},q \right )$
with expectation
$\textrm {Bin} \left ({\xi } b k d^{j},q \right )$
with expectation
Similarly to the previous case, using the Chernoff bound (2.6), we can bound the probability that Hall’s condition fails for such a set B from above by
Taking a union bound over all sets ![]() with
with
![]() $|B| \leq \frac {n}{kd^j}$
as in (3.1), we see that the probability that any such set violates Hall’s condition is at most
$|B| \leq \frac {n}{kd^j}$
as in (3.1), we see that the probability that any such set violates Hall’s condition is at most
![]() $ \frac {1}{6n}$
.
$ \frac {1}{6n}$
.
In the second case when
![]() $b:=|B|> \frac {n}{kd^j}$
, we note that as
$b:=|B|> \frac {n}{kd^j}$
, we note that as ![]() , by Property (A.1) we have
, by Property (A.1) we have
![]() $b \leq \frac {d^j}{{\xi } k}$
and by Property (A.3) we have
$b \leq \frac {d^j}{{\xi } k}$
and by Property (A.3) we have ![]() . Hence,
. Hence, ![]() stochastically dominates a binomial random variable
stochastically dominates a binomial random variable
![]() $\textrm {Bin} \left ({\xi } n,q \right )$
with expectation
$\textrm {Bin} \left ({\xi } n,q \right )$
with expectation
![]() $\mathbb {E}\left [\textrm {Bin} \left ({\xi } n,q \right )\right ]= {\xi } n q \geq 10 \frac {d^j}{{\xi } k}$
. Hence, from (2.6), it follows that
$\mathbb {E}\left [\textrm {Bin} \left ({\xi } n,q \right )\right ]= {\xi } n q \geq 10 \frac {d^j}{{\xi } k}$
. Hence, from (2.6), it follows that
 $$\begin{align*}\mathbb{P}\left[\textrm{Bin} \left( {\xi} n,q \right) <b \right] \leq \mathbb{P}\left[\textrm{Bin} \left({\xi} n,q \right) \leq \frac{d^j}{{\xi} k}\right] \leq e^{-4 d^{j}/({\xi} k) }. \end{align*}$$
$$\begin{align*}\mathbb{P}\left[\textrm{Bin} \left( {\xi} n,q \right) <b \right] \leq \mathbb{P}\left[\textrm{Bin} \left({\xi} n,q \right) \leq \frac{d^j}{{\xi} k}\right] \leq e^{-4 d^{j}/({\xi} k) }. \end{align*}$$
Again, taking a union bound over all sets B of size
![]() $\frac {n}{kd^j} < |B| \leq \frac {d^j}{{\xi } k}$
, we can bound from above the probability that Hall’s condition fails for some B with
$\frac {n}{kd^j} < |B| \leq \frac {d^j}{{\xi } k}$
, we can bound from above the probability that Hall’s condition fails for some B with
![]() $|B| k d^j> n$
from above as in (3.5). Note that in the case
$|B| k d^j> n$
from above as in (3.5). Note that in the case
![]() $j =1$
and
$j =1$
and
![]() $k \geq \frac {\hat {d}}{\log n}$
, we need the additional factor
$k \geq \frac {\hat {d}}{\log n}$
, we need the additional factor
![]() $\left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
for this union bound to work.
$\left \lceil \frac {n}{d^{2j}} \log n \right \rceil $
for this union bound to work.
Hence, for every vertex v, an injection of the desired form exists with probability at least
![]() $1-\frac {1}{3n}$
. Using another union bound over all vertices, we can bound the probability that there exists a vertex for which there is no such injection by
$1-\frac {1}{3n}$
. Using another union bound over all vertices, we can bound the probability that there exists a vertex for which there is no such injection by
![]() $\frac {1}{3}$
, concluding the proof in the case (c).
$\frac {1}{3}$
, concluding the proof in the case (c).
The proof in the case (b) is again analogous, using
![]() $q= \frac {10}{{\xi } kd^j} \log n$
. Since the calculations are similar in nature to cases (a), (c), and (d), we omit them.
$q= \frac {10}{{\xi } kd^j} \log n$
. Since the calculations are similar in nature to cases (a), (c), and (d), we omit them.
Theorem 1.5 then follows by checking that in each regime the bounds given by Theorem 1.6 are not significantly larger than
![]() $\sqrt {\frac {n}{k}}$
.
$\sqrt {\frac {n}{k}}$
.
Proof of Theorem 1.5
Let
![]() $j \in \mathbb {N}$
be such that the average degree
$j \in \mathbb {N}$
be such that the average degree
![]() $d:=d(G)$
of G falls into one of the regimes defined in Theorem 1.6. We note that the upper bound in regimes (1) and (3) is increasing in d and the upper bound in regimes (2) and (4) is decreasing in d. Hence, the bound obtained by applying Theorem 1.6 to G is at least as good as the bound given at the beginning of regime (2), where
$d:=d(G)$
of G falls into one of the regimes defined in Theorem 1.6. We note that the upper bound in regimes (1) and (3) is increasing in d and the upper bound in regimes (2) and (4) is decreasing in d. Hence, the bound obtained by applying Theorem 1.6 to G is at least as good as the bound given at the beginning of regime (2), where
![]() $d = \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
, or at the beginning of regime (4), where
$d = \left (\frac {n}{k}\right )^{\frac {1}{2j}}$
, or at the beginning of regime (4), where
![]() $d = (nk)^{\frac {1}{2j}}$
.
$d = (nk)^{\frac {1}{2j}}$
.
In the first case, the cop number is bounded from above by
 $$\begin{align*}c\left(G\right) \leq 20 {\xi}^{-2} \frac{n}{k d^j}\log n = 20 {\xi}^{-2} \frac{n}{k }\sqrt{\frac{k}{n}}\log n= 20 {\xi}^{-2} \sqrt{\frac{n}{k}} \log n, \end{align*}$$
$$\begin{align*}c\left(G\right) \leq 20 {\xi}^{-2} \frac{n}{k d^j}\log n = 20 {\xi}^{-2} \frac{n}{k }\sqrt{\frac{k}{n}}\log n= 20 {\xi}^{-2} \sqrt{\frac{n}{k}} \log n, \end{align*}$$
and in the second case by
4 Proof of Theorem 1.7
To show the existence of a
![]() ${\xi } \in (0,1]$
such that whp
${\xi } \in (0,1]$
such that whp
![]() $G^k(n,p)$
is
$G^k(n,p)$
is
![]() $\xi $
-expanding, we will proceed as follows: First, we will show that
$\xi $
-expanding, we will proceed as follows: First, we will show that
![]() $G^k(n,p)$
expands very well (in terms of the expansion constant) in the first edge-neighborhood and in the first vertex-neighborhood. Then we will inductively use these results to extend the expansion properties to larger distance neighborhoods. As might be expected, the expansion constant remains quite good until the neighborhoods come close to containing the whole graph. We begin by showing that the first edge-neighborhoods of subsets of
$G^k(n,p)$
expands very well (in terms of the expansion constant) in the first edge-neighborhood and in the first vertex-neighborhood. Then we will inductively use these results to extend the expansion properties to larger distance neighborhoods. As might be expected, the expansion constant remains quite good until the neighborhoods come close to containing the whole graph. We begin by showing that the first edge-neighborhoods of subsets of
![]() $G^k(n,p)$
expand well. In fact, for our inductive step, it will be necessary to show a stronger property that unless a subset A is too large, the size of its first edge-neighborhood will be quite tightly concentrated around the value
$G^k(n,p)$
expand well. In fact, for our inductive step, it will be necessary to show a stronger property that unless a subset A is too large, the size of its first edge-neighborhood will be quite tightly concentrated around the value
![]() $\frac {\hat {d}}{k} |A|$
, where we recall from (2.3) that
$\frac {\hat {d}}{k} |A|$
, where we recall from (2.3) that
![]() $\hat {d} = pk\binom {n-1}{k-1}$
. In order to get good estimates in larger neighborhoods, we need to calculate the deviation in the first neighborhood quite precisely. To this end, we set
$\hat {d} = pk\binom {n-1}{k-1}$
. In order to get good estimates in larger neighborhoods, we need to calculate the deviation in the first neighborhood quite precisely. To this end, we set

Lemma 4.1 Assume the parameters of
![]() $G= G^k(n,p)$
are such that
$G= G^k(n,p)$
are such that
![]() $\frac {\hat {d}}{k} = \omega \left (\log ^3 n \right )$
and
$\frac {\hat {d}}{k} = \omega \left (\log ^3 n \right )$
and
![]() $k \leq \frac {n}{4}$
. Then whp the following holds:
$k \leq \frac {n}{4}$
. Then whp the following holds:
For every subset
![]() $A \subseteq [n]$
satisfying
$A \subseteq [n]$
satisfying
![]() $|A| \leq \frac {2 n}{k \log n}$
,
$|A| \leq \frac {2 n}{k \log n}$
,

Moreover, for every subset
![]() $A \subseteq [n]$
,
$A \subseteq [n]$
,

Proof We will start by proving the first statement. Let
![]() $A \subseteq [n]$
be given where
$A \subseteq [n]$
be given where
![]() $a:= |A| \leq \frac {2 n}{k \log n}$
and let
$a:= |A| \leq \frac {2 n}{k \log n}$
and let ![]() denote the number of edges in G that contain at least one vertex of A. Let us write
denote the number of edges in G that contain at least one vertex of A. Let us write
![]() ${M}$
for the number of edges meeting A in the complete k-uniform hypergraph
${M}$
for the number of edges meeting A in the complete k-uniform hypergraph
![]() $K^k(n)$
on n vertices. A standard inclusion–exclusion type argument implies that
$K^k(n)$
on n vertices. A standard inclusion–exclusion type argument implies that
 $$\begin{align*}{M}= \sum_{j =1}^{\min_{} \left\{ a,k\right\}} \binom{a}{j} \binom{n-j}{k-j} (-1)^{j+1}.\end{align*}$$
$$\begin{align*}{M}= \sum_{j =1}^{\min_{} \left\{ a,k\right\}} \binom{a}{j} \binom{n-j}{k-j} (-1)^{j+1}.\end{align*}$$
The (absolute) ratio of consecutive terms in the sum is given as
 $$ \begin{align} \frac{\binom{a}{j} \binom{n-j}{k-j}}{\binom{a}{j-1} \binom{n-j+1}{k-j+1}} = \frac{(a-j+1) (k-j+1)}{ j(n-j+1)} < \frac{a k}{n} \leq \frac{1}{2}, \quad \text{for all } 2 \leq j \leq \min_{} \left\{ a,k\right\}. \end{align} $$
$$ \begin{align} \frac{\binom{a}{j} \binom{n-j}{k-j}}{\binom{a}{j-1} \binom{n-j+1}{k-j+1}} = \frac{(a-j+1) (k-j+1)}{ j(n-j+1)} < \frac{a k}{n} \leq \frac{1}{2}, \quad \text{for all } 2 \leq j \leq \min_{} \left\{ a,k\right\}. \end{align} $$
Hence,
![]() ${M}$
is dominated by the first term of the sum and the total contribution from all latter terms is at most an
${M}$
is dominated by the first term of the sum and the total contribution from all latter terms is at most an
![]() $O\left (\frac {ak}{n} \right )$
-fraction of this value. More formally,
$O\left (\frac {ak}{n} \right )$
-fraction of this value. More formally,
 $$\begin{align*}M = \sum_{j =1}^{\min\{a,k\}} \binom{a}{j} \binom{n-j}{k-j} (-1)^{j+1} = a \binom{n-1}{k-1} \left(1 + O\left(\frac{ak}{n} \right)\right). \end{align*}$$
$$\begin{align*}M = \sum_{j =1}^{\min\{a,k\}} \binom{a}{j} \binom{n-j}{k-j} (-1)^{j+1} = a \binom{n-1}{k-1} \left(1 + O\left(\frac{ak}{n} \right)\right). \end{align*}$$
Since
![]() $X \sim \text {Bin}(M,p)$
, it follows from
$X \sim \text {Bin}(M,p)$
, it follows from ![]() (see (2.3)) and the fact that
(see (2.3)) and the fact that
![]() $\frac {ak}{n}= O\left (\frac {1}{ \log n}\right ) = o(\delta )$
that
$\frac {ak}{n}= O\left (\frac {1}{ \log n}\right ) = o(\delta )$
that
 $$\begin{align*}\mathbb{E}\left[X\right] = Mp = p a \binom{n-1}{k-1} \left(1 + O\left( \frac{1}{\log n}\right)\right) = \frac{a \hat{d}}{k}\left(1 + o(\delta)\right). \end{align*}$$
$$\begin{align*}\mathbb{E}\left[X\right] = Mp = p a \binom{n-1}{k-1} \left(1 + O\left( \frac{1}{\log n}\right)\right) = \frac{a \hat{d}}{k}\left(1 + o(\delta)\right). \end{align*}$$
Hence, by the Chernoff bound (2.4), it follows that
 $$\begin{align*}\mathbb{P}\left[\left|X-\frac{a\hat{d}}{k}\right|> \frac{a\hat{d} {\delta} }{k}\right] \leq 2 \exp \left(-\frac{a \hat{d} {\delta}^2}{3k} \right). \end{align*}$$
$$\begin{align*}\mathbb{P}\left[\left|X-\frac{a\hat{d}}{k}\right|> \frac{a\hat{d} {\delta} }{k}\right] \leq 2 \exp \left(-\frac{a \hat{d} {\delta}^2}{3k} \right). \end{align*}$$
Therefore, by a union bound, the probability that there exists a set
![]() $A \subseteq [n]$
with
$A \subseteq [n]$
with
![]() $|A| \leq \frac {2 n}{k \log n}$
such that
$|A| \leq \frac {2 n}{k \log n}$
such that ![]() differs from
differs from
![]() $|A|\frac {\hat {d}}{k}$
by more than
$|A|\frac {\hat {d}}{k}$
by more than
![]() $\frac {|A|\hat {d} {\delta }}{k}$
is at most
$\frac {|A|\hat {d} {\delta }}{k}$
is at most
 $$\begin{align*}\sum_{a = 1}^{\frac{2 n}{k \log n}} 2 \binom{n}{a} \exp \left(-\frac{ a \hat{d} {\delta}^2}{3k} \right) \leq \sum_{a = 1}^\infty 2 n^a n^{-a \omega (1)} = o(1), \end{align*}$$
$$\begin{align*}\sum_{a = 1}^{\frac{2 n}{k \log n}} 2 \binom{n}{a} \exp \left(-\frac{ a \hat{d} {\delta}^2}{3k} \right) \leq \sum_{a = 1}^\infty 2 n^a n^{-a \omega (1)} = o(1), \end{align*}$$
where we used our assumption that
![]() $\frac {\hat {d}}{k } = \omega \left (\log ^3 n\right ) = \omega \left ({\delta }^{-2} \log n \right )$
. Therefore, whp
$\frac {\hat {d}}{k } = \omega \left (\log ^3 n\right ) = \omega \left ({\delta }^{-2} \log n \right )$
. Therefore, whp

To show the second statement, we split into two cases. First, let us assume that
![]() $a:=|A| \leq \frac {n}{2k}$
. Let X and
$a:=|A| \leq \frac {n}{2k}$
. Let X and
![]() ${M}$
be defined as above and note that by our assumption on the size of A (4.3) still holds. Hence,
${M}$
be defined as above and note that by our assumption on the size of A (4.3) still holds. Hence,
![]() ${M}$
is an alternating sum with decreasing terms, and therefore is bounded from below by the difference of the first two terms, and it follows from (4.3) that
${M}$
is an alternating sum with decreasing terms, and therefore is bounded from below by the difference of the first two terms, and it follows from (4.3) that
Again, since
![]() $X \sim \text {Bin}(M,p)$
and using
$X \sim \text {Bin}(M,p)$
and using ![]() , we have
, we have
 $$ \begin{align*} \mathbb{E}\left[X\right] = M p \geq p \frac{a}{2} \binom{n-1}{k-1} = \frac{a\hat{d}}{2k}, \end{align*} $$
$$ \begin{align*} \mathbb{E}\left[X\right] = M p \geq p \frac{a}{2} \binom{n-1}{k-1} = \frac{a\hat{d}}{2k}, \end{align*} $$
and hence, by the Chernoff bound (2.5),
 $$\begin{align*}\mathbb{P}\left[X \leq \frac{a\hat{d}}{4k}\right] \leq \mathbb{P}\left[X \leq \frac{1}{2} \mathbb{E}\left[X\right]\right] \leq \exp\left(-\frac{\mathbb{E}\left[X\right]}{8}\right) \leq \exp \left(-\frac{a \hat{d}}{16 k}\right). \end{align*}$$
$$\begin{align*}\mathbb{P}\left[X \leq \frac{a\hat{d}}{4k}\right] \leq \mathbb{P}\left[X \leq \frac{1}{2} \mathbb{E}\left[X\right]\right] \leq \exp\left(-\frac{\mathbb{E}\left[X\right]}{8}\right) \leq \exp \left(-\frac{a \hat{d}}{16 k}\right). \end{align*}$$
Thus, by a union bound, we can bound the probability that there exists a set
![]() $A\subseteq [n]$
with
$A\subseteq [n]$
with
![]() $|A| \leq \frac {n}{2k}$
and
$|A| \leq \frac {n}{2k}$
and ![]() from above by
from above by
 $$\begin{align*}\sum_{a = 1}^{\frac{n}{2k}} \binom{n}{a} \exp \left(-\frac{a \hat{d} }{16 k } \right) \leq \sum_{a= 1}^\infty n^a n^{-a \omega(1)} = o(1), \end{align*}$$
$$\begin{align*}\sum_{a = 1}^{\frac{n}{2k}} \binom{n}{a} \exp \left(-\frac{a \hat{d} }{16 k } \right) \leq \sum_{a= 1}^\infty n^a n^{-a \omega(1)} = o(1), \end{align*}$$
where we used our assumption that
![]() $\frac {\hat {d}}{k} = \omega (\log n)$
. Therefore, whp for every set
$\frac {\hat {d}}{k} = \omega (\log n)$
. Therefore, whp for every set
![]() $A \subseteq [n]$
with
$A \subseteq [n]$
with
![]() $|A| \leq \frac {n}{2k}$
,
$|A| \leq \frac {n}{2k}$
,

If A is such that
![]() $ a> \frac {n}{2k}$
, we pick the largest possible subset
$ a> \frac {n}{2k}$
, we pick the largest possible subset
![]() $A' \subseteq A$
such that
$A' \subseteq A$
such that
![]() $a'k:=|A'| k \leq n/2 $
. Therefore,
$a'k:=|A'| k \leq n/2 $
. Therefore,
![]() $( a'+1)k> n/2$
, and so
$( a'+1)k> n/2$
, and so
![]() $a'k \geq n/2 - k> n/4$
. Using the previous argument and the fact that
$a'k \geq n/2 - k> n/4$
. Using the previous argument and the fact that
![]() $\hat {d} \geq k$
, we see that
$\hat {d} \geq k$
, we see that

In total, the previous two cases yield that whp for all subsets
![]() $A\subseteq [n]$
,
$A\subseteq [n]$
,

To show an analogous result for the vertex-neighborhood, we recall that for a set of edges B we defined
![]() $V_{B} = \{v \in e \colon e \in B\}$
and that the vertex-neighborhood
$V_{B} = \{v \in e \colon e \in B\}$
and that the vertex-neighborhood ![]() of a set A can be written as
of a set A can be written as ![]() . Thus, to show that the first vertex-neighborhood expands well, it will suffices to show that in
. Thus, to show that the first vertex-neighborhood expands well, it will suffices to show that in
![]() $G^k(n,p)$
sets of edges are unlikely to have large overlaps.
$G^k(n,p)$
sets of edges are unlikely to have large overlaps.
Lemma 4.2 Assume the parameters of
![]() $G = G^k(n,p)$
are such that
$G = G^k(n,p)$
are such that
![]() $ k = \omega (\log n) $
,
$ k = \omega (\log n) $
,
![]() $ k \leq 2^{-11} n$
and
$ k \leq 2^{-11} n$
and
![]() $\hat {d} \leq n$
. Then whp the following holds.
$\hat {d} \leq n$
. Then whp the following holds.
For every subset
![]() $B\subseteq E(G)$
of edges and every
$B\subseteq E(G)$
of edges and every
![]() $\epsilon = \epsilon (n) \in \left (0,\frac {1}{2}\right ]$
such that
$\epsilon = \epsilon (n) \in \left (0,\frac {1}{2}\right ]$
such that
![]() $\left (\frac {|B|k}{n}\right )^\epsilon \leq 2^{-5}$
,
$\left (\frac {|B|k}{n}\right )^\epsilon \leq 2^{-5}$
,
Moreover, for every subset
![]() $B\subseteq E(G)$
of edges,
$B\subseteq E(G)$
of edges,
Proof We start by showing the first statement. Let
![]() $b=b(n) \in \mathbb {N}$
and
$b=b(n) \in \mathbb {N}$
and
![]() $\epsilon = \epsilon (n) \in \left (0,\frac {1}{2}\right ]$
be such that
$\epsilon = \epsilon (n) \in \left (0,\frac {1}{2}\right ]$
be such that
![]() $\left (\frac {bk}{n}\right )^\epsilon \leq 2^{-5}$
. We set
$\left (\frac {bk}{n}\right )^\epsilon \leq 2^{-5}$
. We set ![]() and denote by
and denote by
![]() $X_b$
the number of edge sets B in G with
$X_b$
the number of edge sets B in G with
![]() $|B|=b$
and
$|B|=b$
and
![]() $|V_B| \leq t_{b}$
.
$|V_B| \leq t_{b}$
.
To bound the expectation of
![]() $X_b$
, we count the number of possible choices for such an edge set B as follows: We think of B as a partition of the multiset
$X_b$
, we count the number of possible choices for such an edge set B as follows: We think of B as a partition of the multiset
![]() $\hat {V}_B$
, which is given by including each element x of
$\hat {V}_B$
, which is given by including each element x of
![]() $V_B$
with multiplicity equal to the number of edges in B which contain x, into k-sets. In particular, each such edge set B can be specified by fixing the set
$V_B$
with multiplicity equal to the number of edges in B which contain x, into k-sets. In particular, each such edge set B can be specified by fixing the set
![]() $V_B$
of size
$V_B$
of size
![]() $t \leq t_{b}$
, the vector
$t \leq t_{b}$
, the vector
![]() $(x_1,\ldots , x_t)$
determining the multiplicity of each vertex in B, and a partition of the multiset
$(x_1,\ldots , x_t)$
determining the multiplicity of each vertex in B, and a partition of the multiset
![]() $\hat {V}_B$
into b many k-sets.
$\hat {V}_B$
into b many k-sets.
Now, there are at most
![]() $\binom {n}{t}$
many possible sets
$\binom {n}{t}$
many possible sets
![]() $V_B$
and, since
$V_B$
and, since
![]() $\sum _{i=1}^t x_i = bk$
, it follows that there are at most
$\sum _{i=1}^t x_i = bk$
, it follows that there are at most
![]() $\binom {bk+t-1}{t}$
ways to choose the vector
$\binom {bk+t-1}{t}$
ways to choose the vector
![]() $(x_1,\ldots ,x_t)$
. Finally, a crude upper bound for the number of partitions is
$(x_1,\ldots ,x_t)$
. Finally, a crude upper bound for the number of partitions is
![]() $b^{bk}$
, since each of the
$b^{bk}$
, since each of the
![]() $bk$
vertices in
$bk$
vertices in
![]() $\hat {V}_B$
has to be assigned to one of the b many k-sets. It follows that
$\hat {V}_B$
has to be assigned to one of the b many k-sets. It follows that
 $$ \begin{align} \mathbb{E}\left[X_b\right] \leq \sum_{t=1}^{tb} \binom{n}{t}\binom{bk+t-1}{t} b^{bk} p^b. \end{align} $$
$$ \begin{align} \mathbb{E}\left[X_b\right] \leq \sum_{t=1}^{tb} \binom{n}{t}\binom{bk+t-1}{t} b^{bk} p^b. \end{align} $$
Using our assumption that
![]() $\hat {d} \leq n$
, we get that
$\hat {d} \leq n$
, we get that
 $$\begin{align*}p \leq \frac{n}{k \binom{n-1}{k-1}} \leq \frac{n}{k \left(\frac{n-1}{k-1}\right)^{k-1}} \leq \left(\frac{k}{n}\right)^{k-2}, \end{align*}$$
$$\begin{align*}p \leq \frac{n}{k \binom{n-1}{k-1}} \leq \frac{n}{k \left(\frac{n-1}{k-1}\right)^{k-1}} \leq \left(\frac{k}{n}\right)^{k-2}, \end{align*}$$
and hence, using the fact that
![]() $\binom {n}{t}$
is increasing for
$\binom {n}{t}$
is increasing for
![]() $1 \leq t \leq t_{b}$
, we can bound
$1 \leq t \leq t_{b}$
, we can bound
![]() $\mathbb {E}\left [X_b\right ]$
from above by
$\mathbb {E}\left [X_b\right ]$
from above by
 $$ \begin{align*} \mathbb{E}\left[X_b\right] &\leq \sum_{t = 1}^{t_{b}} \binom{n}{t} \binom{bk +t-1}{t} b^{bk} p^b\\ &\leq t_b \left( \frac{en}{t_b} \right)^{t_b} 2^{2bk} b^{bk} \left(\frac{k}{n}\right)^{b(k-2)}\\ &= \left(t_b^{\frac{1}{bk}} \left( \frac{n}{k} \right)^{\frac{2}{k}} \frac{4e^{1-\epsilon}}{(1-\epsilon)^{1-\epsilon} }\left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk}. \end{align*} $$
$$ \begin{align*} \mathbb{E}\left[X_b\right] &\leq \sum_{t = 1}^{t_{b}} \binom{n}{t} \binom{bk +t-1}{t} b^{bk} p^b\\ &\leq t_b \left( \frac{en}{t_b} \right)^{t_b} 2^{2bk} b^{bk} \left(\frac{k}{n}\right)^{b(k-2)}\\ &= \left(t_b^{\frac{1}{bk}} \left( \frac{n}{k} \right)^{\frac{2}{k}} \frac{4e^{1-\epsilon}}{(1-\epsilon)^{1-\epsilon} }\left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk}. \end{align*} $$
However, since
![]() $k=\omega (\log n)$
and
$k=\omega (\log n)$
and
![]() $bk \leq n$
, it follows that
$bk \leq n$
, it follows that
![]() $t_b^{\frac {1}{bk}} \left ( \frac {n}{k} \right )^{\frac {2}{k}} \leq 2$
. Furthermore, it is easy to check that
$t_b^{\frac {1}{bk}} \left ( \frac {n}{k} \right )^{\frac {2}{k}} \leq 2$
. Furthermore, it is easy to check that
![]() $(1-\epsilon )^{(1-\epsilon )}$
is decreasing on
$(1-\epsilon )^{(1-\epsilon )}$
is decreasing on
![]() $\left (0,\frac {1}{2}\right ]$
and hence
$\left (0,\frac {1}{2}\right ]$
and hence
 $$ \begin{align*} \mathbb{E}\left[X_b\right] &\leq \left(\frac{8e}{\sqrt{2} }\left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk} \leq \left(2^4 \left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk} = o\left (\frac{1}{n}\right), \end{align*} $$
$$ \begin{align*} \mathbb{E}\left[X_b\right] &\leq \left(\frac{8e}{\sqrt{2} }\left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk} \leq \left(2^4 \left(\frac{bk}{n}\right)^{\epsilon} \right)^{bk} = o\left (\frac{1}{n}\right), \end{align*} $$
where we used our assumption
![]() $2^4\left (\frac {bk}{n}\right )^{\epsilon } \leq \frac {1}{2}$
and
$2^4\left (\frac {bk}{n}\right )^{\epsilon } \leq \frac {1}{2}$
and
![]() $bk = \omega ( \log n)$
. In particular, since
$bk = \omega ( \log n)$
. In particular, since
![]() $b \leq 2^{-\frac {5}{\epsilon }} \frac {n}{k} \leq n$
, we can conclude by a union bound over all possible values of b that whp there are no edge sets violating the first part of the lemma.
$b \leq 2^{-\frac {5}{\epsilon }} \frac {n}{k} \leq n$
, we can conclude by a union bound over all possible values of b that whp there are no edge sets violating the first part of the lemma.
To show the second statement, suppose that
![]() $B \subseteq E(G)$
is given. If
$B \subseteq E(G)$
is given. If
![]() $|B| \leq \frac {n}{2^{10}k}$
, then
$|B| \leq \frac {n}{2^{10}k}$
, then
 $$\begin{align*}\left( \frac{|B|k}{n}\right)^{\frac{1}{2}} \leq 2^{-5}, \end{align*}$$
$$\begin{align*}\left( \frac{|B|k}{n}\right)^{\frac{1}{2}} \leq 2^{-5}, \end{align*}$$
and so by the first part of the lemma with
![]() $\epsilon =\frac {1}{2}$
, we have
$\epsilon =\frac {1}{2}$
, we have
If
![]() $|B|> \frac {n}{2^{10}k}$
, we simply pick a largest subset
$|B|> \frac {n}{2^{10}k}$
, we simply pick a largest subset
![]() $B' \subset B$
such that
$B' \subset B$
such that
![]() $b' := |B'| \leq \frac {n}{2^{10}k}$
. Then,
$b' := |B'| \leq \frac {n}{2^{10}k}$
. Then,
![]() $b'> \frac {n}{2^{10}k} - 1 \geq \frac {n}{2^{11}k}$
, for large enough n. By the previous observation, it follows that
$b'> \frac {n}{2^{10}k} - 1 \geq \frac {n}{2^{11}k}$
, for large enough n. By the previous observation, it follows that
proving also the second statement.
We note that an immediate corollary of Lemmas 4.1 and 4.2 is that not too large sets in
![]() $G^k(n,p)$
have relatively uniform vertex expansion.
$G^k(n,p)$
have relatively uniform vertex expansion.
Lemma 4.3 Assume that the parameters of
![]() $G = G^k(n,p)$
are such that
$G = G^k(n,p)$
are such that
![]() $\frac {\hat {d}}{k} = \omega (\log ^3 n)$
,
$\frac {\hat {d}}{k} = \omega (\log ^3 n)$
,
![]() $k=\omega (\log n)$
, and
$k=\omega (\log n)$
, and
![]() $\hat {d}\leq n$
. Then whp the following holds. For every subset
$\hat {d}\leq n$
. Then whp the following holds. For every subset
![]() $A \subseteq V(G)$
and every
$A \subseteq V(G)$
and every
![]() $\epsilon =\epsilon (n) \in \left (0,\frac {1}{2}\right ]$
such that
$\epsilon =\epsilon (n) \in \left (0,\frac {1}{2}\right ]$
such that
![]() $\left (\frac {|A| \hat {d}}{n}\right )^{\epsilon } \leq 2^{-6}$
,
$\left (\frac {|A| \hat {d}}{n}\right )^{\epsilon } \leq 2^{-6}$
,
Moreover, for every subset
![]() $A \subseteq [n]$
,
$A \subseteq [n]$
,
Proof We start by showing the first statement. Given a set A and
![]() $\epsilon $
satisfying the conditions of the corollary, we note that, since
$\epsilon $
satisfying the conditions of the corollary, we note that, since
![]() $\hat {d} = \omega \left ( k \log ^3 n\right )$
and
$\hat {d} = \omega \left ( k \log ^3 n\right )$
and
![]() $\epsilon \leq \frac {1}{2}$
,
$\epsilon \leq \frac {1}{2}$
,
 $$\begin{align*}|A| \leq 2^{-\frac{6}{\epsilon}} \frac{n}{\hat{d}} = o\left(\frac{n}{k\log n} \right). \end{align*}$$
$$\begin{align*}|A| \leq 2^{-\frac{6}{\epsilon}} \frac{n}{\hat{d}} = o\left(\frac{n}{k\log n} \right). \end{align*}$$
Hence, we can apply the first part of Lemma 4.1 to conclude that whp

If we let ![]() , then it is immediate that
, then it is immediate that
On the other hand, by (4.9) and our assumption on
![]() $|A|$
,
$|A|$
,
 $$\begin{align*}\left(\frac{|B|k}{n}\right)^{\epsilon} \leq \left( \left(1+{\delta}\right)|A|\frac{\hat{d}}{n}\right)^{\epsilon} \leq 2 \left(|A|\frac{\hat{d}}{n}\right)^{\epsilon} \leq 2^{-5}. \end{align*}$$
$$\begin{align*}\left(\frac{|B|k}{n}\right)^{\epsilon} \leq \left( \left(1+{\delta}\right)|A|\frac{\hat{d}}{n}\right)^{\epsilon} \leq 2 \left(|A|\frac{\hat{d}}{n}\right)^{\epsilon} \leq 2^{-5}. \end{align*}$$
Hence, we can apply Lemma 4.2 to conclude that
as claimed.
To show the second statement, let
![]() $A \subseteq [n]$
and assume first that
$A \subseteq [n]$
and assume first that
![]() $|A| \hat {d} \leq 2^{-12}n.$
Then, by the first statement with
$|A| \hat {d} \leq 2^{-12}n.$
Then, by the first statement with
![]() $\epsilon = \frac {1}{2}$
,
$\epsilon = \frac {1}{2}$
,
showing the second statement in this case. On the other hand, for
![]() $|A| \hat {d}> 2^{-12}n$
, note first the trivial upper bound
$|A| \hat {d}> 2^{-12}n$
, note first the trivial upper bound
For the lower bound, we can apply the second part of Lemma 4.1 to conclude that

Setting ![]() , it now follows from Lemma 4.2 that
, it now follows from Lemma 4.2 that
concluding the proof.
Note that, in particular, Lemma 4.3 implies that ![]() is roughly
is roughly
![]() $\hat {d}$
for every vertex v of
$\hat {d}$
for every vertex v of
![]() $G^k(n,p)$
. To prove Theorem 1.7, we will first show that neighborhoods in
$G^k(n,p)$
. To prove Theorem 1.7, we will first show that neighborhoods in
![]() $G^k(n,p)$
expand well in terms of
$G^k(n,p)$
expand well in terms of
![]() $\hat {d}$
and then finally conclude by showing that d is whp close to
$\hat {d}$
and then finally conclude by showing that d is whp close to
![]() $\hat {d}$
.
$\hat {d}$
.
Proof of Theorem 1.7
We note first that by our assumptions on k and p,
![]() $G^k(n,p)$
satisfies the conditions of Lemmas 4.1–4.3. We therefore assume in what follows that the conclusions of these lemmas hold deterministically in
$G^k(n,p)$
satisfies the conditions of Lemmas 4.1–4.3. We therefore assume in what follows that the conclusions of these lemmas hold deterministically in
![]() $G^k(n,p)$
.
$G^k(n,p)$
.
For
![]() $i \in \{1,2,3\}$
, we say a graph G satisfies Property
$i \in \{1,2,3\}$
, we say a graph G satisfies Property
![]() $\mathbf {(A. i)}$
’, if there exists a constant
$\mathbf {(A. i)}$
’, if there exists a constant
![]() $0 < \xi ^{\prime }_i \leq 1$
such that G satisfies Property
$0 < \xi ^{\prime }_i \leq 1$
such that G satisfies Property
![]() $\mathbf {(A.i)}$
for this constant, but when d is replaced by
$\mathbf {(A.i)}$
for this constant, but when d is replaced by
![]() $\hat {d}$
in Definition 2.1. We will start by showing that
$\hat {d}$
in Definition 2.1. We will start by showing that
![]() $G^k(n,p)$
satisfies the Properties
$G^k(n,p)$
satisfies the Properties
![]() $\mathbf {(A.i)}$
’. Taking a minimum over all respective constants, we obtain a universal constant
$\mathbf {(A.i)}$
’. Taking a minimum over all respective constants, we obtain a universal constant
![]() $\xi '$
such that G satisfies all properties
$\xi '$
such that G satisfies all properties
![]() $\mathbf {(A.i)}$
’ for this constant. We conclude by showing that
$\mathbf {(A.i)}$
’ for this constant. We conclude by showing that
![]() $\hat {d}$
lies sufficiently close to d and in particular that properties
$\hat {d}$
lies sufficiently close to d and in particular that properties
![]() $\mathbf {(A.i)}$
’ imply properties
$\mathbf {(A.i)}$
’ imply properties
![]() $\mathbf {(A.i)}$
for a universal constant
$\mathbf {(A.i)}$
for a universal constant
![]() $\xi $
that is only a constant factor smaller than
$\xi $
that is only a constant factor smaller than
![]() $\xi '$
.
$\xi '$
.
Our first step will be to show that the size of the vertex-neighborhoods in
![]() $G^k(n,p)$
grow relatively uniformly for small enough sets, by inductively applying Lemma 4.3. However, we will need to carefully pick the parameter
$G^k(n,p)$
grow relatively uniformly for small enough sets, by inductively applying Lemma 4.3. However, we will need to carefully pick the parameter
![]() $\epsilon $
in each step so that the cumulative error in these approximations is not too large.
$\epsilon $
in each step so that the cumulative error in these approximations is not too large.
Let
![]() $A \subseteq [n]$
with
$A \subseteq [n]$
with
![]() $a := |A|$
and let
$a := |A|$
and let
![]() $r \in \mathbb {N}$
be such that
$r \in \mathbb {N}$
be such that
![]() $a\hat {d}^r \leq \frac {n}{2 \log n}$
. Note that, since
$a\hat {d}^r \leq \frac {n}{2 \log n}$
. Note that, since
![]() $\hat {d} = \omega \left ( \log ^4 n\right )$
, it follows that
$\hat {d} = \omega \left ( \log ^4 n\right )$
, it follows that
![]() $r \leq \frac {\log n}{4 \log \log n}$
. Our aim will be to show the following:
$r \leq \frac {\log n}{4 \log \log n}$
. Our aim will be to show the following:
In particular, note that if we take
![]() $A=\{v\}$
to be a single vertex, then, since
$A=\{v\}$
to be a single vertex, then, since
![]() $\sqrt {nk} \leq \sqrt {n \frac {\hat {d}}{\log ^3 n}} \leq \frac {n}{2 \log n}$
, it follows from (4.10) that Property (A.1)’ holds for v with
$\sqrt {nk} \leq \sqrt {n \frac {\hat {d}}{\log ^3 n}} \leq \frac {n}{2 \log n}$
, it follows from (4.10) that Property (A.1)’ holds for v with
![]() $\xi _1' = 2$
.
$\xi _1' = 2$
.
In order to apply Lemma 4.3, let us set
![]() $\epsilon _0 = 0$
and
$\epsilon _0 = 0$
and

Note that, since
![]() $a\hat {d}^{i} \leq \frac {n}{2 \log n}$
, it follows that
$a\hat {d}^{i} \leq \frac {n}{2 \log n}$
, it follows that
![]() $\epsilon _i = o(1)$
for each
$\epsilon _i = o(1)$
for each
![]() $i \leq r$
.
$i \leq r$
.
We claim inductively that the following bound holds for each
![]() $0\leq i \leq r$
:
$0\leq i \leq r$
:

where the statement is clear for
![]() $i=0$
.
$i=0$
.
Suppose that (4.12) holds for some
![]() $i <r$
. Then, since
$i <r$
. Then, since
![]() $i < r = o\left ( \frac {1}{{\delta }}\right )$
, we have
$i < r = o\left ( \frac {1}{{\delta }}\right )$
, we have

and so

Hence, we can apply Lemma 4.3 to ![]() to conclude that
to conclude that

and so the induction step holds.
In particular, taking
![]() $i=r$
, it follows from (4.13) that
$i=r$
, it follows from (4.13) that

Hence it remains to bound the term
![]() $\prod _{j=0}^{r}\left (1-\epsilon _j \right )$
. The following claim, whose verification we defer to the end of the proof, provides such a bound.
$\prod _{j=0}^{r}\left (1-\epsilon _j \right )$
. The following claim, whose verification we defer to the end of the proof, provides such a bound.
Claim 3 Let
![]() $a \leq n$
and r be such that
$a \leq n$
and r be such that
![]() $a\hat {d}^r \leq \frac {n}{2 \log n}$
, and let
$a\hat {d}^r \leq \frac {n}{2 \log n}$
, and let
![]() $\epsilon _i$
be defined as in (4.11). Then
$\epsilon _i$
be defined as in (4.11). Then
 $$ \begin{align} \prod_{j=0}^{r}\left(1-\epsilon_j \right) \geq 2^{-4}.\\[-42pt]\nonumber \end{align} $$
$$ \begin{align} \prod_{j=0}^{r}\left(1-\epsilon_j \right) \geq 2^{-4}.\\[-42pt]\nonumber \end{align} $$
It is now clear that (4.14) and Claim 3 together imply (4.10).
Now let us turn to Property (A.2)’. Let us fix a subset
![]() $A \subseteq [n]$
with
$A \subseteq [n]$
with
![]() $a:=|A|$
and
$a:=|A|$
and
![]() $r \in \mathbb {N}$
. We let
$r \in \mathbb {N}$
. We let
![]() $r_0 = \min \Bigl \{ r, \max _{} \left \{ i : |A|\hat {d}^i \leq \frac {n}{2 \log n}\right \}\Bigr \}$
and let
$r_0 = \min \Bigl \{ r, \max _{} \left \{ i : |A|\hat {d}^i \leq \frac {n}{2 \log n}\right \}\Bigr \}$
and let
![]() $A' = N_V^{r_0}(A)$
. Then, by (4.10), we have
$A' = N_V^{r_0}(A)$
. Then, by (4.10), we have
In particular, if
![]() $r=r_0$
, then (4.16) implies that (A.2)’ holds for A with
$r=r_0$
, then (4.16) implies that (A.2)’ holds for A with
![]() $\xi _2'= 2^{-5}$
.
$\xi _2'= 2^{-5}$
.
If
![]() $r = r_0+1$
, then by (4.16) and the second part of Lemma 4.3,
$r = r_0+1$
, then by (4.16) and the second part of Lemma 4.3,
implying that Property (A.2)’ holds for A with
![]() ${\xi }_2' = 2^{-21}$
. Finally, for
${\xi }_2' = 2^{-21}$
. Finally, for
![]() $r \geq r_0+2$
, note that since
$r \geq r_0+2$
, note that since
![]() $\hat {d} = \omega (\log ^3 n)$
, we have
$\hat {d} = \omega (\log ^3 n)$
, we have
![]() $a\hat {d}^r \geq n$
, and so applying the second part of Lemma 4.3 to
$a\hat {d}^r \geq n$
, and so applying the second part of Lemma 4.3 to ![]() yields together with (4.17)
yields together with (4.17)
and hence Property (A.2)’ holds also in this case with
![]() ${\xi }_2' = 2^{-37}$
.
${\xi }_2' = 2^{-37}$
.
Let us finally turn to Property (A.3)’. Let
![]() $B \subseteq E(G)$
. By the second part of Lemma 4.2, we conclude that
$B \subseteq E(G)$
. By the second part of Lemma 4.2, we conclude that
However, since
![]() $N_V^r(B) = N_V^r(V_B)$
, we can apply (A.2)’ to
$N_V^r(B) = N_V^r(V_B)$
, we can apply (A.2)’ to
![]() $V_B$
to conclude that
$V_B$
to conclude that

and hence
![]() $G^k(n,p)$
satisfies Property (A.3)’ with
$G^k(n,p)$
satisfies Property (A.3)’ with
![]() $\xi ^{\prime }_3=2^{-49}$
. It remains to show that Properties
$\xi ^{\prime }_3=2^{-49}$
. It remains to show that Properties
![]() $\mathbf {(A.i)}$
’ imply Properties
$\mathbf {(A.i)}$
’ imply Properties
![]() $\mathbf {(A.i)}$
. To this end, we note that if
$\mathbf {(A.i)}$
. To this end, we note that if
![]() $r_1 = \max _{} \left \{ i : d^i \leq n\right \}$
, then it is sufficient to show that Properties
$r_1 = \max _{} \left \{ i : d^i \leq n\right \}$
, then it is sufficient to show that Properties
![]() $\mathbf {(A.i)}$
hold for all
$\mathbf {(A.i)}$
hold for all
![]() $r \leq r_1$
. It is clear then that the result follows from the following claim, which we again verify at the end of the proof.
$r \leq r_1$
. It is clear then that the result follows from the following claim, which we again verify at the end of the proof.
Claim 4 For all
![]() $r \leq r_1$
, we have
$r \leq r_1$
, we have
This completes the proof.
It remains to prove Claims 3 and 4.
Proof of Claim 3
Note first that as
![]() $\epsilon _j \leq \frac {1}{2}$
for all
$\epsilon _j \leq \frac {1}{2}$
for all
![]() $1 \leq j \leq r$
, we can estimate the product as
$1 \leq j \leq r$
, we can estimate the product as
 $$ \begin{align} \prod_{j=0}^{r}\left(1-\epsilon_j \right) = \prod_{j=1}^{r}\left(1-\epsilon_j \right)\geq \exp\biggl(-2 \sum_{j=1}^{r} \epsilon_j \biggr). \end{align} $$
$$ \begin{align} \prod_{j=0}^{r}\left(1-\epsilon_j \right) = \prod_{j=1}^{r}\left(1-\epsilon_j \right)\geq \exp\biggl(-2 \sum_{j=1}^{r} \epsilon_j \biggr). \end{align} $$
By reversing the order of summation, we can write this sum as
 $$ \begin{align} \sum_{j=1}^{r} \epsilon_j &= \sum_{j=1}^{r} \frac{5}{\log n -\log \left(2a\hat{d}^{j} \right)} = 5\sum_{j=1}^{r} \frac{1}{\log n - \log \left(2a\hat{d}^{r-j+1} \right)}. \end{align} $$
$$ \begin{align} \sum_{j=1}^{r} \epsilon_j &= \sum_{j=1}^{r} \frac{5}{\log n -\log \left(2a\hat{d}^{j} \right)} = 5\sum_{j=1}^{r} \frac{1}{\log n - \log \left(2a\hat{d}^{r-j+1} \right)}. \end{align} $$
To bound the term
![]() $\log \left (2a\hat {d}^{r-j+1} \right )$
from above, we first note that since
$\log \left (2a\hat {d}^{r-j+1} \right )$
from above, we first note that since
![]() $a\hat {d}^r \leq \frac {n}{2\log n}$
, we have
$a\hat {d}^r \leq \frac {n}{2\log n}$
, we have
 $$ \begin{align*} \log \left(2a\hat{d}^{r} \right) \leq \log \left(\frac{n}{\log n} \right) = \log n -\log \log n. \end{align*} $$
$$ \begin{align*} \log \left(2a\hat{d}^{r} \right) \leq \log \left(\frac{n}{\log n} \right) = \log n -\log \log n. \end{align*} $$
Furthermore, since
![]() $\hat {d} = \omega \left (k \log ^3 n\right ) = \omega \left ( \log ^4 n\right )$
, it follows that for all
$\hat {d} = \omega \left (k \log ^3 n\right ) = \omega \left ( \log ^4 n\right )$
, it follows that for all
![]() $j\in \mathbb {N}$
,
$j\in \mathbb {N}$
,
which, together with the previous equation, yields that
Combining this bound with (4.20), we obtain
 $$ \begin{align} \sum_{j=1}^{r_0} \epsilon_j \leq 5 \sum_{j=1}^{r_0} \frac{1}{(4j-3) \log \log n} \leq \frac{5}{\log \log n} \left(1+ \sum_{j=1}^{r_0} \frac{1}{ 4j} \right) \leq \frac{5}{4} \cdot \frac{5+\log r_0}{\log \log n} \leq \frac{5}{4}, \end{align} $$
$$ \begin{align} \sum_{j=1}^{r_0} \epsilon_j \leq 5 \sum_{j=1}^{r_0} \frac{1}{(4j-3) \log \log n} \leq \frac{5}{\log \log n} \left(1+ \sum_{j=1}^{r_0} \frac{1}{ 4j} \right) \leq \frac{5}{4} \cdot \frac{5+\log r_0}{\log \log n} \leq \frac{5}{4}, \end{align} $$
where the penultimate inequality comes from a standard bound on the harmonic sum and the last inequality uses
![]() $r_0 \leq \frac {\log n}{e^5}$
. Plugging (4.21) into (4.19), we obtain
$r_0 \leq \frac {\log n}{e^5}$
. Plugging (4.21) into (4.19), we obtain
 $$\begin{align*}\prod_{j=0}^{r_0}\left(1-\epsilon_j \right) \geq \exp\left(-\frac{5}{2}\right) \geq \frac{1}{2^4}, \end{align*}$$
$$\begin{align*}\prod_{j=0}^{r_0}\left(1-\epsilon_j \right) \geq \exp\left(-\frac{5}{2}\right) \geq \frac{1}{2^4}, \end{align*}$$
which concludes the proof of Claim 3.
Proof of Claim 4
Clearly, it is sufficient to prove the claim for
![]() $r=r_1$
, and we note that
$r=r_1$
, and we note that
![]() $r_1 \geq 1$
, since
$r_1 \geq 1$
, since
![]() $\hat {d} \leq n$
. If
$\hat {d} \leq n$
. If
![]() $r_1$
=
$r_1$
=
![]() $1$
, we get from Property (A.2)’
$1$
, we get from Property (A.2)’
which immediately implies (4.18).
Otherwise, note that for each vertex
![]() $v \in [n]$
and each
$v \in [n]$
and each
![]() $\epsilon \in \left (0,\frac {1}{2}\right ]$
such that
$\epsilon \in \left (0,\frac {1}{2}\right ]$
such that
![]() $\left (\frac {\hat {d}}{n}\right )^\epsilon \leq 2^{-6}$
, we have by Lemma 4.3 that
$\left (\frac {\hat {d}}{n}\right )^\epsilon \leq 2^{-6}$
, we have by Lemma 4.3 that
Therefore, recalling that ![]() , we have
, we have
As
![]() $r_0 \geq 2$
, it follows that
$r_0 \geq 2$
, it follows that
![]() $\hat {d} \leq \sqrt {n}$
and so we can take
$\hat {d} \leq \sqrt {n}$
and so we can take
![]() $\epsilon = {\delta }$
and by (4.22) obtain the following:
$\epsilon = {\delta }$
and by (4.22) obtain the following:
5 Concluding discussion
In Theorem 1.5, we prove Conjecture 1.4 for
![]() $G^k(n,p)$
in dense regimes up to a
$G^k(n,p)$
in dense regimes up to a
![]() $\log $
-factor. It would be interesting to remove this
$\log $
-factor. It would be interesting to remove this
![]() $\log $
-factor to match the conjectured bound. We note that in the case of
$\log $
-factor to match the conjectured bound. We note that in the case of
![]() $G(n,p)$
, Prałat and Wormald [Reference Prałat and Wormald24] gave a two-stage cop strategy with similarities to the vertex surrounding strategy of Łuczak and Prałat [Reference Łuczak and Prałat21] to show that Meyniel’s Conjecture holds whp in
$G(n,p)$
, Prałat and Wormald [Reference Prałat and Wormald24] gave a two-stage cop strategy with similarities to the vertex surrounding strategy of Łuczak and Prałat [Reference Łuczak and Prałat21] to show that Meyniel’s Conjecture holds whp in
![]() $G(n,p)$
in the dense regime. Similar ideas might be of use in order to remove this
$G(n,p)$
in the dense regime. Similar ideas might be of use in order to remove this
![]() $\log $
-factor.
$\log $
-factor.
Furthermore, our theorems give upper bounds on the cop number. It would be interesting to know if these upper bounds are close to tight. Łuczak and Prałat [Reference Łuczak and Prałat21] gave an escape strategy for the Robber which matches their upper bound up to logarithmic factors, which also uses in a critical way the regular (vertex-)expansion properties of
![]() $G(n,p)$
. However, while there are already some technical issues to overcome with extending their analysis of such a strategy to the case of
$G(n,p)$
. However, while there are already some technical issues to overcome with extending their analysis of such a strategy to the case of
![]() $G^k(n,p)$
with
$G^k(n,p)$
with
![]() $k = \omega (1)$
, the robber must also have to take into account in some way the “edge-expansion” of
$k = \omega (1)$
, the robber must also have to take into account in some way the “edge-expansion” of
![]() $G^k(n,p)$
, as we know there are regimes of p where the cops can do strictly better than the bounds given by the vertex surrounding strategy. Hence, some new ideas will be necessary to find a corresponding robber strategy in the hypergraph game.
$G^k(n,p)$
, as we know there are regimes of p where the cops can do strictly better than the bounds given by the vertex surrounding strategy. Hence, some new ideas will be necessary to find a corresponding robber strategy in the hypergraph game.
More generally, it seems the game of Cops and Robber on hypergraphs has been much less well studied than the graphical counterpart. In particular, it would be interesting to find some natural classes of hypergraphs on which the cop number is bounded. Motivated by the classic result of Aigner and Fromme [Reference Aigner and Fromme2] on the cop number of planar graphs, it is natural to ask such questions in relation to geometric notions of embeddability.
However, even in the case
![]() $k=3$
, it is clear that there are k-graphs which are embeddable without crossings in
$k=3$
, it is clear that there are k-graphs which are embeddable without crossings in
![]() $\mathbb {R}^k$
but have arbitrary large cop number. Hence, in order to bound the cop number, we need to make further assumptions on the structure of the k-graphs, and a natural one in the case of
$\mathbb {R}^k$
but have arbitrary large cop number. Hence, in order to bound the cop number, we need to make further assumptions on the structure of the k-graphs, and a natural one in the case of
![]() $3$
-graphs would be to ask that the
$3$
-graphs would be to ask that the
![]() $3$
-graph, when viewed as a two-dimensional simplicial complex, is simply connected.
$3$
-graph, when viewed as a two-dimensional simplicial complex, is simply connected.
Question 5.1 Is there a constant K such that every simply connected
![]() $3$
-graph G which can be embedded without crossings in
$3$
-graph G which can be embedded without crossings in
![]() $\mathbb {R}^3$
satisfies
$\mathbb {R}^3$
satisfies
![]() $c(G) \leq K$
?
$c(G) \leq K$
?
For simply connected
![]() $3$
-graphs, it is known that embeddability in
$3$
-graphs, it is known that embeddability in
![]() $\mathbb {R}^3$
, as with Kuratowski’s theorem, has a characterization in terms of excluded minors [Reference Carmesin8, Reference Carmesin9], here in terms of space minors. In the case of graphs, a result of Andreae [Reference Andreae3] shows that excluding a fixed minor bounds the cop number of a graph, and it would be interesting to know if, for an appropriate notion of minor, this also holds for the hypergraph game.
$\mathbb {R}^3$
, as with Kuratowski’s theorem, has a characterization in terms of excluded minors [Reference Carmesin8, Reference Carmesin9], here in terms of space minors. In the case of graphs, a result of Andreae [Reference Andreae3] shows that excluding a fixed minor bounds the cop number of a graph, and it would be interesting to know if, for an appropriate notion of minor, this also holds for the hypergraph game.
Question 5.2 Let H be a fixed k-graph. Does there exist a constant
![]() $K:=K(H)$
such that every k-graph G with no H-“minor” satisfies
$K:=K(H)$
such that every k-graph G with no H-“minor” satisfies
![]() $c(G) \leq K$
?
$c(G) \leq K$
?
Finally, we note that there are perhaps other natural ways to extend the game of Cops and Robber to the hypergraph setting. One particularly natural variant would be to play the game on the edges of the hypergraph, rather than the vertices. That is, the cops and robber live on the edges of the hypergraph and are allowed to move to incident edges, instead of adjacent vertices. Let us denote the minimum number of cops needed to win in the edge-game on G by
![]() $c_e(G)$
. In the case of graphs, the edge-game was considered by Dudek, Gordinowicz, and Prałat [Reference Dudek, Gordinowicz and Prałat12], who showed that it is closely related to the vertex-game, in that for any graph G,
$c_e(G)$
. In the case of graphs, the edge-game was considered by Dudek, Gordinowicz, and Prałat [Reference Dudek, Gordinowicz and Prałat12], who showed that it is closely related to the vertex-game, in that for any graph G,
 $$ \begin{align} \left\lceil \frac{c(G)}{2} \right\rceil \leq c_e(G) \leq c(G)+1. \end{align} $$
$$ \begin{align} \left\lceil \frac{c(G)}{2} \right\rceil \leq c_e(G) \leq c(G)+1. \end{align} $$
In particular,
![]() $c(G)$
and
$c(G)$
and
![]() $c_e(G)$
cannot differ by more than a fixed multiplicative constant. In the hypergraph game, it is less clear whether
$c_e(G)$
cannot differ by more than a fixed multiplicative constant. In the hypergraph game, it is less clear whether
![]() $c(G)$
and
$c(G)$
and
![]() $c_e(G)$
can have wildly different behavior.
$c_e(G)$
can have wildly different behavior.
Question 5.3 Is there a function
![]() $f:\mathbb {N} \rightarrow \mathbb {R}$
such that for any k-graph G,
$f:\mathbb {N} \rightarrow \mathbb {R}$
such that for any k-graph G,
Acknowledgements
This work is the result of the fourth author’s visit of TU Graz under Oberwolfach’s Simons Visiting Professors program in December 2021. This research was funded in whole or in part by the Austrian Science Fund (FWF) [10.55776/{W1230, P36131, I6502}]. For open access purposes, the author has applied a CC BY public copyright license to any author-accepted manuscript version arising from this submission.