Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-08T16:34:39.098Z Has data issue: false hasContentIssue false
  • English
  • Français

Chromatic Solutions

Published online by Cambridge University Press:  20 November 2018

W. T. Tutte
W. T. Tutte*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Early in the Seventies I sought the number of rooted λ-coloured triangulations of the sphere with 2p faces. In these triangulations double joins, but not loops, were permitted. The investigation soon took the form of a discussion of a certain formal power series l(y, z, λ) in two independent variables y and z.

The basic theory of l is set out in [1]. There l is defined as the coefficient of x2 in a more complicated power series g(x, y, z, λ). But the definition is equivalent to the following formula.

1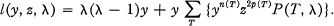

Here T denotes a general rooted triangulation. n(T) is the valency of its root-vertex, and 2p(T) is the number of its faces. P(T, λ) is the chromatic polynomial of the graph of T.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 741 - 758
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Tutte, W. T., Chromatic sums for rooted planar triangulations: the cases λ = 1 and λ = 2, Can. J. Math. 25 (1973), 426–447.Google Scholar
2. Tutte, W. T., Chromatic sums for rooted planar triangulations II: the case λ = ⸆ +• l, Can. J. Math. 25 (1973), 657–671.Google Scholar
3. Tutte, W. T., Chromatic sums for rooted planar triangulations III: the case λ = 3, Can. J. Math. 25 (1973), 780–790.Google Scholar
4. Tutte, W. T., Chromatic sums for rooted planar triangulations V: special equations, Can. J. Math. 26 (1974), 893–907.Google Scholar
5. Tutte, W. T., On a pair of functional equations of combinatorial interest, Aequationes Math. 17 (1978), 121–140.Google Scholar