Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-08T18:36:46.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Classes of Positive Definite Unimodular Circulants

Published online by Cambridge University Press:  20 November 2018

Morris Newman  and
Olga Taussky
Morris Newman
Affiliation:
National Bureau of Standards, Washington 25, D.C.
Olga Taussky
Affiliation:
National Bureau of Standards, Washington 25, D.C.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All matrices considered here have rational integral elements. In particular some circulants of this nature are investigated. An n × n circulant is of the form

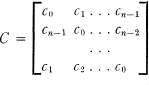
The following result concerning positive definite unimodular circulants was obtained recently (3 ; 4 ):

Let C be a unimodular n × n circulant and assume that C = AA' where A is an n × n matrix and A' its transpose. Then it follows that C = C1C1', where C1 is again a circulant.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 9 , 1957 , pp. 71 - 73
Copyright
Copyright © Canadian Mathematical Society 1957

References

1. Minkowski, H., Grundlagen für eine Théorie der quadratischen Formen mit ganzzahligec Koeffizienten, Gesammelte Abhandlungen 1 (1911), 3–144.Google Scholar
2. Mordell, L. J., The definite quadratic forms in 8 variables with determinant unity, J. de Math. pures et appliquées, 17 (1938), 41–46.Google Scholar
3. Newman, M. and Taussky, O., On a generalization of the normal basis in abelian algebrain number fields, Comm. on Pure and Applied Math. 9 (1956), 85–91.Google Scholar
4. Taussky, O., Unimodular integral circulants, Math. Zeitschr. 63 (1955), 286–289.Google Scholar