Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-07T04:23:34.632Z Has data issue: false hasContentIssue false
  • English
  • Français

The Classical N-body Problem in the Context of Curved Space

Published online by Cambridge University Press:  20 November 2018

Florin Diacu
Florin Diacu*
Affiliation:
Pacific Institute for the Mathematical Sciences and, Department of Mathematics and Statistics, University of Victoria, P.O. Box 1700 STN CSC, Victoria, BC, Canada, V8W 2Y2 e-mail: diacu@uvic.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide the differential equations that generalize the Newtonian 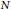$N$-body problem of celestial mechanics to spaces of constant Gaussian curvature 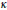$\kappa $, for all $\kappa \in \mathbb{R}$. In previous studies, the equations of motion made sense only for 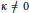$\kappa \ne 0$. The system derived here does more than just include the Euclidean case in the limit 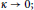$\kappa \to 0;$ it recovers the classical equations for 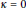$\kappa =0$. This new expression of the laws of motion allows the study of the 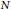$N$-body problem in the context of constant curvature spaces and thus oòers a natural generalization of the Newtonian equations that includes the classical case. We end the paper with remarks about the bifurcations of the first integrals.

Keywords

N-body problemspaces of constant curvature
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 4 , 01 August 2017 , pp. 790 - 806
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bertrand, J., Théorème relatif au mouvement d'un point attiré vers un center fixe. C. R. Acad. Sci. 77(1873), 849–853.Google Scholar
[2] Bolyai, W. and Bolyai, J., Geometrische Untersuchungen. Hrsg. P. Stäckel, Teubner, Leipzig, 1913.Google Scholar
[3] Bruns, H., Über die Intégrale des Vielkörper- (1887), 25–96.http://dx.doi.org/10.1007/BF02612319 Google Scholar
[4] Diacu, F., On the singularities of the curved N-body problem. Trans. Amer. Math. Soc. 363(2011),no. 4, 2249–2264.http://dx.doi.org/10.1090/S0002-9947-2010-05251-1 Google Scholar
[5] Diacu, F., Polygonal homographie orbits of the curved 3-body problem. Trans. Amer. Math. Soc. 364(2012), 2783–2802.http://dx.doi.org/10.1090/S0002-9947-2011-05558-3 Google Scholar
[6] Diacu, F., Relative equilibria of the curved N-body problem. Atlantis Studies in Dynamical Systems,1. Atlantis Press, Amsterdam, 2012.Google Scholar
[7] Diacu, F., The non-existence of the center-of-mass and the linear-momentum integrals in the curved N-body problem. Libertas Math. (NS) 32(2012), no. 1, 25–37.Google Scholar
[8] Diacu, F., Relative equilibria of the 3-dimensional curved n-body problem. Memoirs Amer. Math. Soc. 228(2013), no. 1071.Google Scholar
[9] Diacu, F., The curved N-body problem: risks and rewards,. Math. Intelligencer 35(2013), no .3, 24–33.http://dx.doi.org/10.1007/s00283-013-9397-1 Google Scholar
[10] Diacu, F. and Kordlou, S., Rotopukators of the curved N-body problem. J. Differential Equations 255(2013), 2709–2750.http://dx.doi.Org/10.1016/j.jde.2013.07.009 Google Scholar
[11] Diacu, F., Martinez, R., Pérez-Chavela, E., andSimó, C., On the stability of tetrahedral relative equilibria in the positively curved 4-body problem. Physica D 256–257(2013), 21–35.http://dx.doi.Org/10.1016/j.physd.2O13.04.007 Google Scholar
[12] Diacu, F. and Pérez-Chavela, E., Homographie solutions of the curved 3-body problem. J. Differential Equations 250(2011), 340–366. http://dx.doi.Org/10.1016/j.jde.2O10.08.011 Google Scholar
[13] Diacu, F., Pérez-Chavela, E., and Santoprete, M., Saari's conjecture for the collinear N-body problem. Trans. Amer. Math. Soc. 357(2005), no. 10, 4215–4223.http://dx.doi.Org/10.1090/S0002-9947-04-03606-2 Google Scholar
[14] Diacu, F., The N-body problem in spaces of constant curvature. Part I: Relative equilibria. J. Nonlinear Sci. 22(2012), no. 2, 247–266. http://dx.doi.Org/10.1007/s00332-011-911 6-z Google Scholar
[15] Diacu, F. The N-body problem in spaces of constant curvature. Part II:Singularities. J. Nonlinear Sci. 22(2012), no. 2, 267–275, http://dx.doi.org/10.1007/s00332-011-911 7-y Google Scholar
[16] Diacu, F., Pérez-Chavela, E., and Reyes, J. G. Victoria, An intrinsic approach in the curved N-body problem. The negative curvature case. J. Differential Equations 252(2012), 4529–4562.http://dx.doi.Org/10.1016/j.jde.2O12.01.002 Google Scholar
[17] Diacu, F. and Thorn, B., Rectangular orbits of the curved 4-body problem. Proc. Amer. Math. Soc. 143(2015), 1583–1593.http://dx.doi.org/10.1090/S0002-9939-2014-12326-4 Google Scholar
[18] Dubrovin, B., Fomenko, A., and Novikov, P., Modern geometry, methods and applications. Vol. I, Springer-Verlag, New York, 1984.Google Scholar
[19] Euler, L., Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. In: Opera Omnia, 10. Birkhäuser, 1980.Google Scholar
[20] Goe, G., Comments on Miller's “The myth of Gauss-s experiment on the Euclidean nature of physical space”. Isis 65(1974), no. 1, 83–87.http://dx.doi.Org/10.1086/351220 Google Scholar
[21] Halsted, G. B., Gauss and non-Euclidean geometry. Amer. Math. Monthly 7(1900), no. 11, 247–252.http://dx.doi.Org/10.2307/2968396 Google Scholar
[22] Liebmann, H., Die Kegelschnitte und die Planetenbewegung im nichteuklidischen Raum. Berichte Königl. Sächsischen Gesell. Wiss., Math. Phys. Klasse 54(1902), 393–423.Google Scholar
[23] Liebmann, H., Über die Zentralbewegung in der nichteuklidische Geomtrie. Berichte Königl. Sächsischen Gesell. Wiss., Math. Phys. Klasse 55(1903), 146–153.Google Scholar
[24] Lobachevsky, N. I., The new foundations of geometry with full theory of parallels. 1835–1838, In: Collected works, Vol. 2, GITTL, Moscow, 1949, p. 159.Google Scholar
[25] Pérez-Chavela, E. and Reyes, J. G. Victoria, An intrinsic approach in the curved N-body problem. The positive curvature case. Trans. Amer. Math. Soc. 364(2012), no. 7, 3805–3827.http://dx.doi.org/10.1090/S0002-9947-2012-05563-2 Google Scholar
[26] Shchepetilov, A. V., Nonintegrability of the two-body problem in constant curvature spaces. J. Phys.A: Math. Gen. 39(2006), 5787–5806; corrected version at arxiv:math.DS/0601382 http://dx.doi.org/10.1088/0305-4470/39/20/011 Google Scholar