No CrossRef data available.
Article contents
Cluster Sets of Functions on an N-Ball
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let Dn be the open unit ball in En, and let Sn be the n-sphere. The cluster set C(f, p) of a function f : Dn —> Sn at a point p on the boundary of Dn is the set of points y in Sn such that there exists a sequence of points xm —> p, xm in Dn, with f(xm) —> y. Given an arc γ in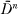 
, meeting the boundary bdy(Dn) only in p, the arc cluster set C(f, γ) is the set of points y in Sn such that there exists a sequence xm —> p, xm in γ, with f(xm) —> y.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1963
References
1.
Bers, L., On a theorem of Mori and the definition of quasi-conformality, Trans. Amer. Math . Soc, 84 (1957), 77–84.Google Scholar
2.
Callender, E. D., Holder continuity of n-dimensional quasi-conformal mappings, Technical Report No. 81, Stanford University (1959).Google Scholar
3.
Church, P. T., Extensions of Stoilow's theorem, J. London Math. Soc, 37 (1962), 86–89.Google Scholar
4.
Gross, W., Uber die Singularitàten analytischer Funktionen, Monatsh. Math, und Phys., 29 (1918), 1–47.Google Scholar
6.
Smale, S., A classification of immersions of the two-sphere, Trans. Amer. Math. Soc, 90 (1959), 281–290.Google Scholar
7.
Weigand, L., Über die Randwerte meromorpher Funktionen einer Verdnderlichen, Comment. Math. Helv., 22, 2 (1949), 125–149.Google Scholar
You have
Access