Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-07T06:34:31.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Codimension 2 Symmetric Homoclinic Bifurcations and Application to 1:2 Resonance

Published online by Cambridge University Press:  20 November 2018

Chengzhi Li  and
Christiane Rousseau
Chengzhi Li
Affiliation:
Peking University, Beijing, People's Republic of China
Christiane Rousseau
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

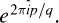In this paper we study a codimension 3 form of the 1:2 resonance. It was first noted by Arnold [3] that the study of bifurcations of symmetric vector fields under a rotation of order q yields information about Hopf bifurcation for a fixed point of a planar diffeomorphism F with eigenvalues . The map Fq can be identified to arbitrarily high order with the flow map of a symmetric vector field having a double-zero eigenvalue ([3], [4], [10], [23]). The resonance of order 2 (also called 1:2 resonance) considered here is the case of a pair of eigenvalues —1 with a Jordan block of order 2. The diffeomorphism then has normal form around the origin given by [4]:

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 2 , 01 April 1990 , pp. 191 - 212
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Andronov, A.A., Leontovich, E.A., Gordon, I.I. and Meier, A.G., Theory of bifurcations of dynamical systems in the plane, Israel program of scientific translations, Jerusalem (1971).Google Scholar
2. Arnold, V.I., Lectures on bifurcations and versai families, Russian Math. Surveys 27 (1972), 53-123.Google Scholar
3. Arnold, V.I., Loss of stability of self-oscillations close to resonances and versa! deformations of equivariant vector fields, Funct. Anal. Appl. 11 (1977), 1–10.Google Scholar
4. Arnold, V.I., Geometric methods in the theory of ordinary differential equations (Springer-Verlag, New York, Heidelberg, Berlin, 1982), (Russian original, 1977).Google Scholar
5. Bogdanov, R.I., Bifurcation of a limit cycle for a family of vector fields on the plane, Trudy Seminar Petrovskii (1976), (in Russian), Sel. Math. Sov. / (1981) (in English), 373–387.Google Scholar
6. Bogdanov, R.I., Versai deformation of a singular point of a vector field on the plane in the case of zero eigenvalues, Trudy Seminar Petrovskii (1976), (in Russian), Sel. Math. Sov. 1 (1981) (in English), 388–421.Google Scholar
7. Carr, J., Applications of center manifolds (Springer-Verlag, New York, Heidelberg, Berlin, 1981 ).Google Scholar
8. Chenciner, A., Bifurcation de points fixes elliptiques. I Courbes invariantes, Publ. Math. IHES 65 (1985), 67-127.Google Scholar
9. Chenciner, A., Bifurcation de points fixes elliptiques. II Orbites périodiques et ensembles de Cantor invariants, Inventiones Math. 80 (1985), 81–106.Google Scholar
10. Chow, S.N., Li, C. and Wang, D., Center manifolds, normal forms and bifurcations of vector fields, book, in preparation.Google Scholar
11. Dumortier, F., Roussarie, R. and Sotomayor, J., Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part. The cusp case of codimension 3, Ergodic Theory Dynamical Systems 7 (1987), 375–413.Google Scholar
12. Dumortier, F., Generic 3-parameter families of planar vector fields on the plane, unfoldings of saddle, focus and elliptic singularities with nilpotent linear parts, preprint (1988).Google Scholar
13. Guckenheimer, J., and Holmes, P., Nonlinear oscillations, dynamical systems and bifurcations of vector fields (Springer-Verlag, New York, Heidelberg, Berlin, 1983).Google Scholar
14. Horozov, E.I., Versai deformations of equivariant vector fields under symmetries of order 2 and 3, Trudy Seminar Petrovskii 5 (1979), 163–192.Google Scholar
15. Joyal, P., The cusp of order n, to appear in J. Differential Equations.Google Scholar
16. Lassalle, M.G., Une démonstration du théorème de division pour les fonctions différentiables, Topology 12 (1973), 41–62.Google Scholar
17. Li, Chengzhi and Rousseau, C., A system with three limit cycles appearing in a Hopf bifurcation and dying in a homoclinic bifurcation. The cusp of order 4, J. of Differential Equations 79 (1989), 132–167.Google Scholar
18. Mardesic, P., The number of limit cycles of polynomial deformations of a Hamiltonian vector field, preprint (1988).Google Scholar
19. Petrov, G.S., Elliptic integrals and their nonoscillation, Funct. Anal. Appl. 20 (1986), 37–40.Google Scholar
20. Poenaru, V., Analyse différentielle, Springer Lecture Notes 371 (Springer-Verlag, New York, Heidelberg, Berlin, 1974).Google Scholar
21. Roussarie, R., On the number of limit cycles which appear by perturbation of separatrix loop of planar vector fields, Bol. Soc. Bras. Mat. 17 (1986), 67–101.Google Scholar
22. Roussarie, R., Déformations génériques des cusps, Astérisque 150-151 (1987), 151–184.Google Scholar
23. Rousseau, C., Codimension 1 and 2 bifurcations of fixed points of diffeomorphisms and of periodic orbits of vector fields, to appear in Annales Mathématiques du Québec.Google Scholar
24. Shi, Songling, A method of constructing cycles without contact around a weak focus, J. of Differential Equations 41 (1981), 301-320.Google Scholar
25. Takens, F., Forced oscillations and bifurcations, in Applications of global analysis /, Comm. Math. Inst. Rijksuniversiteit Utrecht (1974), 1–59.Google Scholar
26. Takens, F., Singularities of vector fields, Publ. Math. I.H.E.S. 43 (1974), 47–100.Google Scholar