Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-01T19:19:55.526Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugacy Classes and Nilpotent Variety of a Reductive Monoid

Published online by Cambridge University Press:  20 November 2018

Mohan S. Putcha
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We continue in this paper our study of conjugacy classes of a reductive monoid $M$. The main theorems establish a strong connection with the Bruhat-Renner decomposition of $M$. We use our results to decompose the variety 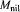${{M}_{\text{nil}}}$ of nilpotent elements of $M$ into irreducible components. We also identify a class of nilpotent elements that we call standard and prove that the number of conjugacy classes of standard nilpotent elements is always finite.

Keywords

20G9920M1014M9920F55
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 829 - 843
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Carter, R. W., Finite groups of Lie type: Conjugacy classes and complex characters. Wiley, 1985.Google Scholar
2. Humphreys, J. E., Reflection groups and Coxeter groups. Cambridge Univ. Press, 1990.Google Scholar
3. Lusztig, G., On the finiteness of the number ofunipotent classes. Invent. Math. 34(1976), 201-213.Google Scholar
4. Pennell, E. A., Putcha, M. S. and Renner, L. E., Analogue of the Bruhat-Chevally order for reductive monoids. J. Algebr. 196(1997), 339-368.Google Scholar
5. Putcha, M. S., Regular linear algebraic monoids. Trans. Amer. Math. Soc. 290(1985), 615-626.Google Scholar
6. Putcha, M. S., Linear algebraic monoids. London Math. Soc., Lecture Note Series 133, Cambridge Univ. Press, 1988.Google Scholar
7. Putcha, M. S., Conjugacy classes in algebraic monoids. Trans. Amer. Math. Soc. 303(1987), 529—540.Google Scholar
8. Putcha, M. S., Conjugacy classes in algebraic monoids II. Canad. J. Math. 46(1994), 648-661.Google Scholar
9. Putcha, M. S. and Renner, L. E., The system ofidempotents and the lattice of J-classes of reductive algebraic monoids. J. Algebr. 116(1988), 385-399.Google Scholar
10. The canonical compactification of a finite group of Lie type. Trans. Amer. Math. Soc. 337(1993), 305-319.Google Scholar