Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-08T16:47:28.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugates of Infinite Measure Preserving Transformations

Published online by Cambridge University Press:  20 November 2018

S. Alpern ,
J. R. Choksi  and
V. S. Prasad
S. Alpern
Affiliation:
London School of Economics, London, Great Britain
J. R. Choksi
Affiliation:
McGill University, Montreal, Quebec
V. S. Prasad
Affiliation:
York University, North York, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider a question concerning the conjugacy class of an arbitrary ergodic automorphism σ of a sigma finite Lebesgue space (X, 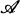, μ) (i.e., a is a ju-preserving bimeasurable bijection of (X, 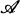, μ). Specifically we prove

THEOREM 1. Let τ, σ be any pair of ergodic automorphisms of an infinite sigma finite Lebesgue space (X, 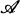, μ). Let F be any measurable set such that

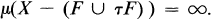
Then there is some conjugate σ' of σ such that σ'(x) = τ(x) for μ-almost every x in F.

The requirement that F ∪ τF has a complement of infinite measure is, for example, satisfied when F has finite measure, and in that case, the theorem was proved by Choksi and Kakutani ([7], Theorem 6).

Conjugacy theorems of this nature have proved to be very useful in proving approximation results in ergodic theory. These conjugacy results all assert the denseness of the conjugacy class of an ergodic (or antiperiodic) automorphism in various topologies and subspaces.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 3 , 01 June 1988 , pp. 742 - 749
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Ahlfors, L. and Sario, L., Riemann surfaces (Princeton University Press, Princeton, New Jersey, 1965).Google Scholar
2. Alpern, S., A topological analogue of Halmos’ conjugacy lemma, Inventiones Math. 48 (1978), 1–6.Google Scholar
3. Alpern, S., Return times and conjugates of an antiperiodic transformation, Erg. Th. and Dyn. Sys. 1 (1981), 135–143.Google Scholar
4. Alpern, S. and Prasad, V. S., End behaviour and ergodicity for homeomorphisms of manifolds with finitely many ends, Can. J. Math. 39 (1987), 473–491.Google Scholar
5. Alpern, S. and Prasad, V. S., Dynamics induced on the ends of a non-compact manifold, Erg. Th. and Dyn. Sys. 8 (1988), 1–15.Google Scholar
6. Alpern, S. and Prasad, V. S., Weak mixing manifold homeomorphisms preserving an infinite measure, Can. J. Math. 59 (1987), 1475–1488.Google Scholar
7. Choksi, J. R. and Kakutani, S., Residuality of ergodic measurable transformations and of ergodic transformations which preserve an infinite measure, Indiana Univ. Math. J. 28 (1979), 453–469.Google Scholar
8. Friedman, N., Introduction to ergodic theory (Van Nostrand Studies in Math. 29, New York, 1970).Google Scholar
9. Halmos, P., Lectures on ergodic theory (Chelsea, New York, 1956).Google Scholar
10. Krengel, U., Entropy of conservative transformations, Z. fur Wahrsch. u. Verw. Geb. 7 (1967), 161–181.Google Scholar
11. Sachdeva, U., On the category of mixing in infinite measure spaces, Math. Systems Th. 5 (1971), 319–330.Google Scholar