Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-08T21:05:39.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Dense Subalgebras of Left Hilbert Algebras

Published online by Cambridge University Press:  20 November 2018

A. van Daele
A. van Daele*
Affiliation:
Celestijnenlaan, Heverlee, Belgium
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a von Neumann algebra acting on a Hilbert space 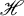and assume that M has a separating and cyclic vector ω in 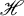. Then it can happen that M contains a proper von Neumann subalgebra N for which ω is still cyclic. Such an example was given by Kadison in [4]. He considere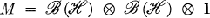d and 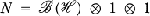acting on 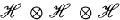where 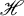is a separable Hilbert space. In fact by a result of Dixmier and Maréchal, M, M′ and N have a joint cyclic vector [3]. Also Bratteli and Haagerup constructed such an example ([2], example 4.2) to illustrate the necessity of one of the conditions in the main result of their paper. In fact this situation seems to occur rather often in quantum field theory (see [1] Section 24.2, [3] and [4]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 6 , 01 December 1982 , pp. 1245 - 1250
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Bogolubov, N., Lagunov, A. and Todorov, I., Introduction to axiomatic quantum field theory (Benjamin, Reading, Mass., 1975).Google Scholar
2. Bratelli, O. and Haagerup, U., Unbounded derivations and invariant states, Comm. Math. Phys. 59 (1978), 79–95.Google Scholar
3. Dixmier, J. and O, Maréchal, Vecteurs totalisateurs d'une algèbre de von Neumann, Comm. Math. Phys. 22 (1971), 44–50.Google Scholar
4. Kadison, R., Remarks on the type of von Neumann algebras of local observables in quantum field theory, J. Math. Phys. 4 (1963), 1511–1516.Google Scholar
5. Skau, C., Finite subalgebras of a von Neumann algebra, J. Funct. Anal. 25 (1977), 211–235.Google Scholar
6. Takesaki, M., Tomitd's theory of modular Hilbert algebras and its applications, Springer Lecture Notes in Mathematics 128 (1970).Google Scholar
7. Van Daele, A., Fixed points and commutation theorems, Springer Lecture Notes in Mathematics 650 (1978), 140–144.Google Scholar
8. Van Daele, A., On pairs of closed operators, preprint, Leuven (1981).Google Scholar