Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T21:46:00.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Derivations from Hereditary Subalgebras of C*-Algebras

Published online by Cambridge University Press:  20 November 2018

A. J. Lazar ,
S.-K. Tsui  and
S. Wright
A. J. Lazar
Affiliation:
Tel-Aviv University, Tel-Aviv, Israel
S.-K. Tsui
Affiliation:
Oakland University, Rochester, Michigan
S. Wright
Affiliation:
Oakland University, Rochester, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a C*-algebra, B a C*-subalgebra of A, δ:B → A a derivation, i.e., a linear map with

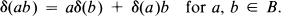
There has been considerable interest for several years now in the question of when δ can be extended from B to a derivation of A (see, for example, [8], Section 4, [1], [5], [4], [6], [9], [10], [11]). The paper before the reader will be concerned with this extension problem when B is a hereditary C*-subalgebra of A.

Our work takes its cue from the paper [6] of George Elliott. We prove in Section 2 of the present paper that derivations as described above of a unital hereditary C*-subalgebra always extend whenever A is either simple, AW*, separable and AF, or separable with continuous trace, thus generalizing and extending Theorem 4.5 of [6].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 1 , 01 February 1986 , pp. 109 - 126
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Akemann, C. A. and Johnson, B. E., Derivations of nonseparable C*-algebras, J. Funct. Anal. 33 (1979), 311–331.Google Scholar
2. Akemann, C. A., Pedersen, G. K. and Tomiyama, J., Multipliers of C*-algebras, J. Funct. Anal. 13 (1973), 277–301.Google Scholar
3. Berberian, S. K., Baer *-rings (Springer-Verlag, New York, 1972).CrossRefGoogle Scholar
4. Christensen, E., Extensions of derivations, I, II, J. Funct. Anal. 27 (1978), 234–247; Math. Scand. 50 (1982), 111–122.Google Scholar
5. Elliott, G., Derivations of matroid C*-algebras, Invent. Math. 9 (1970), 253–269.Google Scholar
6. Elliott, G., On lifting and extending derivations of approximately finite-dimensional C*-algebras, J. Funct. Anal. 17 (1974), 395–408.Google Scholar
7. Elliott, G., Automorphisms determined by multipliers on ideals of a C*-algebra, J. Funct. Anal. 25 (1976), 1–10.Google Scholar
8. Kaplansky, I., Algebraic and analytic aspects of operator algebras, C.B.M.S. Regional Conference Series in Mathematics, No. 1 (Providence, Rhode Island, 1970).CrossRefGoogle Scholar
9. Lazar, A. J., Tsui, S.-K. and Wright, S., Derivations from subalgebras of separable C*-algebras, Michigan Math. J. 31 (1984), 65–72.Google Scholar
10. Lazar, A. J., Tsui, S.-K. and Wright, S., Derivations from subalgebras of C*-algebras with continuous trace, to appear in Rocky Mt. J. Math.Google Scholar
11. Lazar, A. J., Tsui, S.-K. and Wright, S., A cohomological characterization of finite-dimensional C*-algebras, to appear in J. Operator Theory.Google Scholar
12. Lazar, A. J. and Taylor, D., Approximately finite-dimensional C*-algebras and Bratteli diagrams, Trans. Amer. Math. Soc. 259 (1980), 599–619.Google Scholar
13. Olesen, D., Derivations of AW*-algebras are inner, Pacific J. Math. 53 (1974), 555–561.Google Scholar
14. Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, London – New York – San Francisco, 1979).Google Scholar