Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bollobás, Béla
1981.
The diameter of random graphs.
Transactions of the American Mathematical Society,
Vol. 267,
Issue. 1,
p.
41.
Bollobás, Béla
and
Fernandez de la Vega, W.
1982.
The diameter of random regular graphs.
Combinatorica,
Vol. 2,
Issue. 2,
p.
125.
Bollobás, Béla
and
Klee, Victor
1984.
Diameters of random bipartite graphs.
Combinatorica,
Vol. 4,
Issue. 1,
p.
7.
Philips, T.K.
Towsley, D.F.
and
Wolf, J.K.
1990.
On the diameter of a class of random graphs.
IEEE Transactions on Information Theory,
Vol. 36,
Issue. 2,
p.
285.
Walley, S.K.
Tan, H.H.
and
Viterbi, A.M.
1994.
Limit distributions for the diameter and the shortest path hop count in random graphs with positive integer edge costs.
p.
618.
Chung, Fan
and
Lu, Linyuan
2001.
The Diameter of Sparse Random Graphs.
Advances in Applied Mathematics,
Vol. 26,
Issue. 4,
p.
257.
Mahdian, Mohammad
and
Xu, Ying
2007.
Algorithms and Models for the Web-Graph.
Vol. 4863,
Issue. ,
p.
179.
Lattanzi, Silvio
Panconesi, Alessandro
and
Sivakumar, D.
2011.
Milgram-routing in social networks.
p.
725.
Mahdian, Mohammad
and
Xu, Ying
2011.
Stochastic kronecker graphs.
Random Structures & Algorithms,
Vol. 38,
Issue. 4,
p.
453.
Kim, Myunghwan
and
Leskovec, Jure
2012.
Multiplicative Attribute Graph Model of Real-World Networks.
Internet Mathematics,
Vol. 8,
Issue. 1-2,
p.
113.
HEGARTY, PETER
and
ZHELEZOV, DMITRII
2014.
On the Diameters of Commuting Graphs Arising from Random Skew-Symmetric Matrices.
Combinatorics, Probability and Computing,
Vol. 23,
Issue. 3,
p.
449.
Kim, Younjin
Kumbhat, Mohit
Nagy, Zoltán Lóránt
Patkós, Balázs
Pokrovskiy, Alexey
and
Vizer, Máté
2015.
Identifying codes and searching with balls in graphs.
Discrete Applied Mathematics,
Vol. 193,
Issue. ,
p.
39.
Krzywdziński, K.
and
Rybarczyk, K.
2015.
Distributed algorithms for random graphs.
Theoretical Computer Science,
Vol. 605,
Issue. ,
p.
95.
Nazeer, Waqas
Kang, Shin
Nazeer, Saima
Munir, Mobeen
Kousar, Imrana
Sehar, Ammara
and
Kwun, Young
2016.
On Center, Periphery and Average Eccentricity for the Convex Polytopes.
Symmetry,
Vol. 8,
Issue. 12,
p.
145.
Bastos, Lucas
Ochi, Luiz Satoru
Protti, Fábio
Subramanian, Anand
Martins, Ivan César
and
Pinheiro, Rian Gabriel S.
2016.
Efficient algorithms for cluster editing.
Journal of Combinatorial Optimization,
Vol. 31,
Issue. 1,
p.
347.
Fraiman, Nicolas
and
Mitsche, Dieter
2017.
Extended Abstracts Summer 2015.
Vol. 6,
Issue. ,
p.
41.
Barter, Edmund
and
Gross, Thilo
2017.
Spatial effects in meta-foodwebs.
Scientific Reports,
Vol. 7,
Issue. 1,
Chatterjee, Soumyottam
Fathi, Reza
Pandurangan, Gopal
and
Pham, Nguyen Dinh
2018.
Fast and Efficient Distributed Computation of Hamiltonian Cycles in Random Graphs.
p.
764.
Fraiman, Nicolas
and
Mitsche, Dieter
2018.
The diameter of inhomogeneous random graphs.
Random Structures & Algorithms,
Vol. 53,
Issue. 2,
p.
308.
Tavara, Shirin
and
Schliep, Alexander
2021.
Effects of network topology on the performance of consensus and distributed learning of SVMs using ADMM.
PeerJ Computer Science,
Vol. 7,
Issue. ,
p.
e397.
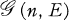 denote the set of all loopless undirected graphs with the node-set {1, …, n} and exactly E edges.
denote the set of all loopless undirected graphs with the node-set {1, …, n} and exactly E edges.



