Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-08T23:53:17.337Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and Regularization of the Kepler Problem on Surfaces of Constant Curvature

Published online by Cambridge University Press:  20 November 2018

Jaime Andrade ,
Nestor Dàvila ,
Ernesto Pérez-Chavela  and
Claudio Vidal
Jaime Andrade
Affiliation:
Departamento de Matemática, Facultad de Ciencias, Universidad de Bio-Bio, Casilla 5-C, Concepciόn, VIII-regiόn, Chile e-mail: jandrade@ubiobio.cl
Nestor Dàvila
Affiliation:
Departamento de Matemática, Facultad de Ciencias, Universidad de Bio-Bio, Casilla 5-C, Concepciόn, VIII-regiόn, Chile e-mail: ndavila@ubiobio.cl
Ernesto Pérez-Chavela
Affiliation:
Departamento de Matemática, Instituto Tecnolόgico Autόnomo de México, (ITAM), Río Hondo 1, Col. Progreso Tizapán, Ciudad de México, 01080, México e-mail: ernesto.perez@itam.mx
Claudio Vidal
Affiliation:
Grupo de Investigaciόn en Sistemas Dinámicos y Aplicaciones-GISDA, Departamento de Matemática, Facultad de Ciencias, Universidad de Bio-BioCasilla 5-,Concepciόn, VIII-regiόn, Chile e-mail: clvidal@ubiobio.cl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

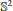We classify and analyze the orbits of the Kepler problem on surfaces of constant curvature (both positive and negative, ${{\mathbb{S}}^{2}}$ and 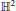${{\mathbb{H}}^{2}}$, respectively) as functions of the angular momentum and the energy. Hill's regions are characterized, and the problem of time-collision is studied. We also regularize the problem in Cartesian and intrinsic coordinates, depending on the constant angular momentum, and we describe the orbits of the regularized vector field. The phase portraits both for 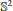${{\mathbb{S}}^{2}}$ and 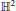${{\mathbb{H}}^{2}}$ are pointed out.

Keywords

70F1670G60Kepler problem on surfaces of constant curvatureHill's regionsingularitiesregularizationqualitative analysis of ODE
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 5 , 01 October 2017 , pp. 961 - 991
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Boccaletti, D. and Puccaco, G., Theory of orbits. Vol 1. Integrable systems and non-perturbative methods. Astronomy and Astrophysics Library, Springer-Verlag, Berlin, 1996.Google Scholar
[2] Cariñena, J. F. and Rafiada, M. F., and Santander, M., Central potentials on spaces of constant curvature: the Kepler problem on the two-dimensional sphere S2 and the hyperbolic plane H2. J. Math. Phys. 46(2005), no. 5,052702.http://dx.doi.Org/10.1063/1.1893214 Google Scholar
[3] Celletti, A. Basics of regularization theory. In: Chaotic Worlds: From Order to Disorder in Gravitational N-Body Dynamical Systems, Springer, Netherlands, 2006, pp. 203–230.Google Scholar
[4] Diacu, F., Pérez-Chavela, E., and Santoprete, M., The n-body problem in spaces of constant curvature. arxiv:0807.1747 Google Scholar
[5] Diacu, F., The n-body problem in spaces of constant curvature. Part I: Relative equilibria. J. Nonlinear Sci. 22(2012), no. 2, 247–266.http://dx.doi.org/10.1007/s00332-011-9116-z Google Scholar
[6] Diacu, F., The n-body problem in spaces of constant curvature. Part II: Singularities. J. Nonlinear Sci. 22(2012), no. 2, 267–275.http://dx.doi.org/10.1007/s00332-011-911 7-y Google Scholar
[7] Diacu, F., Relative equilibria of the curved N-body problem. Atlantis Studies in Dynamical Systems, 1, Atlantis Press, Amsterdam, Paris, Beijing, 2012. http://dx.doi.org/10.2 991/978-94-91216-68-8 Google Scholar
[8] Do Carmo, M. P., Differential geometry of curves and surfaces. Prentice-Hall, Inc., Englewood Cliffs, NJ, 1976.Google Scholar
[9] Dubrovin, B. A., Fomenko, A. T., and Novikov, P., Modern geometry-methods and applications. Part I. The geometry of surfaces, transformation groups, and fields. Second ed. Graduate Texts in Mathematics, 93, Springer-Verlag, New York, 1992.http://dx.doi.org/10.1007/978-1-4612-4398-4 Google Scholar
[10] Kozlov, V. V. and Harin, A. O., Kepler's problem in constant curvature spaces. Celestial Mech. Dynam. Astronom. 54(1992), no. 4, 393–399.http://dx.doi.Org/10.1007/BF00049149 Google Scholar
[11] Lacomba, E. A. and Sienra, G., Blow up techniques in the Kepler problem. In: Holomorphic dynamics (Mexico, 1986), Lecture Notes in Math., 1345, Springer, Berlin, 1988, pp. 177–191.http://dx.doi.Org/10.1OO7/BFbOO81402 Google Scholar
[12] Levi-Civita, T., Sur la régularisation du problème des trois corps. Acta Math. 42(1920), 99–144. http://dx.doi.Org/10.1007/BF02404404 Google Scholar
[13] Liebmann, H., Die Kegelschnitte und die Planetenbewegung im nichteuklidischen Raum. Berichte Königl, Sächsischen Gesell. Wiss., Math. Phys. Klasse 54(1902), 393–423.Google Scholar
[14] Martinez, R. and Simό, C., On the stability of the Lagrangian homographie solutions in a curved three body problem on . Discrete Cont. Dyn. Syst. Ser. A. 33(2013), no. 3,1157–1175.Google Scholar
[15] Pollard, H., Introduction to celestial mechanics. The Carus Mathematical Monographs, 18, The Mathematical Association of America, Washington, D.C., 1976.Google Scholar
[16] Shchepetilov, A. V., Nonintegrability of the two-body problem in constant curvature spaces. J. Phys. A 39(2006), no. 20, 5787–5806.http://dx.doi.Org/10.1088/0305-4470/39/20/011 Google Scholar
[17] Stiefel, E. L. and Scheifele, G., Linear and regular celestial mechanics. Perturbed two-body motion, numerical methods, canonical theory. Die Grundlehren der mathematischen Wissenschaften, 174, Springer-Verlag, New York-Heidelberg, 1971.Google Scholar
[18] Story, W E., On non-euclidean properties of conies. Amer. J. Math. 5(1882), no. 1-4, 358–381.http://dx.doi.Org/10.2307/2369551 Google Scholar
[19] Sundman, K. F., Mémoire sur le problème des trois corps. Acta Math. 36(1913), no. 1,105–179.http://dx.doi.org/10.1007/BF02422379 Google Scholar
[20] Szebehely, V., Theory of orbits-the restricted problem of three bodies. Academic Press, New York, 1967.Google Scholar
[21] Tibboel, P., Polygonal homographie orbits in spaces of constant curvature. Proc. Amer. Math. Soc. 141(2013), no. 4, 1465–1471. http://dx.doi.org/10.1090/S0002-9939-2012-11410-8 Google Scholar
[22] Zhu, S., Eulerian relative equilibria of the curved 3-body problems in S2. Proc. Amer. Math. Soc. 142(2014), no. 8, 2837–2848.http://dx.doi.org/10.1090/S0002-9939-2014-11995-2 Google Scholar