Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T01:20:25.956Z Has data issue: false hasContentIssue false
  • English
  • Français

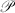Embedding -Like Compacta in Manifolds

Published online by Cambridge University Press:  20 November 2018

Michael C. McCord
Michael C. McCord*
Affiliation:
University of Georgia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A compactum is a compact, metrizable space. A continuum is a connected compactum. All polyhedra will be finitely triangulable spaces. If a is an open cover of a compactum X, a map of X onto a compactum Y is called an α-map provided that the inverse image of each point in Y is contained in some member of α.

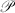If is a class of polyhedra, then, following Mardešić and Segal (10), we say a compactum X is 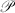-like provided that for each open cover α of X there exists an a-map of X onto some member of .

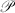Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 321 - 332
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Bennett, R., Embedding products of chainable continua, Proc. Amer. Math. Soc., 16 (1965), 1026–1027.Google Scholar
2. Bing, R. H., Snake-like continua, Duke Math. J., 18 (1951), 653–663.Google Scholar
3. Bing, R. H., Embedding circle-like continua in the plane, Can. J. Math., 14 (1962), 113–128.Google Scholar
4. Eilenberg, S. and Steenrod, N., Foundations of algebraic topology (Princeton, 1952).Google Scholar
5. Fearnley, L., Embeddings of topological products of circularly chainable continua, Amer. Math. Soc. Not., 12 (1965), 480.Google Scholar
6. Hilton, P. J. and Wylie, S., Homology theory (Cambridge, 1960).Google Scholar
7. Isbell, J. R., Embeddings of inverse limits, Ann. Math., 70 (1959), 73–84.Google Scholar
8. Isbell, J. R., Uniform spaces, Mathematical Surveys, 12, Amer. Math. Soc. (Providence, 1964).Google Scholar
9. MacLane, S., Homology (Berlin, 1963).Google Scholar
10. Mardešić, S. and Segal, J., ∈-Mappings onto polyhedra, Trans. Amer. Math. Soc., 109 (1963), 146–164.Google Scholar
11. McCord, M. C., On embedding manifold-like continua in manifolds, Amer. Math. Soc. Not., 12 (1965), 138.Google Scholar
12. McCord, M. C., Universal -like compacta, Michigan Math. J., 13 (1966), 71–85.Google Scholar