Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-06T16:07:10.762Z Has data issue: false hasContentIssue false
  • English
  • Français

Enriques Diagrams and Adjacency of Planar Curve Singularities

Published online by Cambridge University Press:  20 November 2018

Maria Alberich-Carramiñana  and
Joaquim Roé
Maria Alberich-Carramiñana
Affiliation:
Departament de Matemàtica Aplicada I, Universitat Politècnica de Catalunya, Av. Diagonal 647, 08028-Barcelona, Spain E-mail: maria.alberich@upc.es
Joaquim Roé
Affiliation:
Departament de Matemàtiques, Universitat Autonòma de Barcelona, Edifici C, 08193-Bellaterra, Barcelona, Spain e-mail: jroe@mat.uab.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study adjacency of equisingularity types of planar complex curve singularities in terms of their Enriques diagrams. The goal is, given two equisingularity types, to determine whether one of themis adjacent to the other. For linear adjacency a complete answer is obtained, whereas for arbitrary (analytic) adjacency a necessary condition and a sufficient condition are proved. We also obtain new examples of exceptional deformations, i.e, singular curves of type 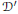${\mathcal{D}}'$ that can be deformed to a curve of type 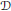$\mathcal{D}$ without 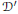${\mathcal{D}}'$ being adjacent to 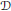$\mathcal{D}$.

Keywords

14B0732S30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 1 , 01 February 2005 , pp. 3 - 16
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Arnold, V. I., Local normal forms of functions, Invent.Math. 35 (1976), 87–109.Google Scholar
[2] Brieskorn, E., Die hierarchie de. 1-modularen singularitäten. (German. English summary), Manuscripta Math. 27 (1979), 183–219.Google Scholar
[3] Casas-Alvero, E., Singularities of plane curves, LondonMath. Soc. Lecture Notes Series, no. 276, Cambridge University Press, 2000.Google Scholar
[4] Cheah, J., The cohomology of smooth nested Hilbert schemes of points, Ph.D. thesis, Chicago, 1994.Google Scholar
[5] Cheah, J., The virtual hodge polynomials of nested Hilbert schemes and related varieties, Math. Z. 227 (1998), no. 3, 479–504.Google Scholar
[6] du Plessis, A. and Wall, C. T. C., The geometry of topological stability, LondonMathematical Society Monographs. New Series, vol. 9, Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar
[7] Enriques, F. and Chisini, O., Lezioni sulla teoria geometrica delle equazioni e delle funzioni algebriche, N. Zanichelli, Bologna, 1915.Google Scholar
[8] Évain, L., Calculs des dimensions de systèmes linéaires de courbes planes par collisions de gros points, C. R. Acad. Sci. Paris 325, I (1997), 1305–1308.Google Scholar
[9] Évain, L., Collisions de trois gros points sur une surface algébrique, Ph.D. thesis, Université de Nice, 1997.Google Scholar
[10] Évain, L., Compactification of configuration spaces via Hilbert schemes, preprint (2001), http://xxx.lanl.gov/abs/math/0107041.Google Scholar
[11] Granja, A. and T. Sánchez-Giralda, Enriques graphs of plane curves., Comm. Algebra 20 (1992), no. 2, 527–562.Google Scholar
[12] Greuel, G. M., Lossen, C., and Shustin, E., Plane curves of minimal degree with prescribed singularities, Invent.Math. 133 (1998), 539–580.Google Scholar
[13] Guseĭn-Zade, S. M. and Nekhoroshev, N. N., Contiguities of singularities Ak to points of the singularity stratu. μ = constant, Functional Anal. Appl. 17 (1983), no. 4, 312–313.Google Scholar
[14] Harbourne, B., Complete linear systems on rational surfaces, Trans. A.M.S. 289 (1985), 213–226.Google Scholar
[15] Kleiman, S. and Piene, R., Enumerating singular curves on surfaces, Proc. Conference on Algebraic Geometry: Hirzebruch 70 (Warsaw 1998), vol. 241, A.M.S. Contemp.Math., 1999, pp. 209–238.Google Scholar
[16] Lossen, C., The geometry of equisingular and equianalytic families of curves on a surface, Ph.D. thesis, Universität Kaiserslautern, 1998.Google Scholar
[17] Nobile, A. and Villamayor, O., Equisingular stratifications associated to families of planar ideals, J. Alg. 193 (1997), 239–259.Google Scholar
[18] Pham, F., Remarque sur l’équisingularité universelle, Preprint, Université de Nice (1970).Google Scholar
[19] Roé, J., Varieties of clusters and Enriques diagrams, Math. Proc. Cambridge Philos. Soc., to appear, http://xxx.lanl.gov/abs/math/0108023.Google Scholar
[20] Roé, J., On the conditions imposed by tacnodes and cusps, Trans. A.M.S. 353 (2001), no. 12, 4925–4948.Google Scholar
[21] Russell, H., Counting singular plane curves via Hilbert schemes, Preprint (2000), http://xxx.lanl.gov/abs/math/0011214.Google Scholar
[22] Shustin, E., Analytic order of singular and critical points, preprint (2002), http://arXiv.org/abs/math.AG/0209043.Google Scholar
[23] Siersma, D., Periodicities in Arnold's lists of singularities, Real and Complex Singularities, Oslo 1976 (P. Holm, ed.), Sijthoff & Noordhoof, 1977, pp. 497–524.Google Scholar
[24] Steenbrink, J. H. M., Semicontinuity of the singularity spectrum, Invent.Math. 79 (1985), no. 3, 557–565.Google Scholar
[25] Steenbrink, J. H. M., The spectrum of hypersurface singularities, Actes du Colloque de Theorie de Hodge (Luminy, 1987), Astérisque, vol. 179–180, 1989, pp. 163–184.Google Scholar
[26] Wahl, J., Equisingular deformations of plane algebroid curves, Trans. A.M.S. 193 (1974), 143–170.Google Scholar
[27] Wall, C. T. C., Notes on the classification of singularities, Proc. LondonMath. Soc. (3) 48 (1984), no. 3, 461–513.Google Scholar
[28] Zariski, O., Studies in equisingularity I, Amer. J. Math. 87 (1965), 507–536.Google Scholar
[29] Zariski, O., Studies in equisingularity II, Amer. J. Math. 87 (1965), 972–1006.Google Scholar