Hostname: page-component-7bb8b95d7b-fmk2r Total loading time: 0 Render date: 2024-09-18T13:26:58.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme Positive Contractions on Finite Dimensional lp-Spaces

Published online by Cambridge University Press:  20 November 2018

Ryszard Grząślewicz
Ryszard Grząślewicz*
Affiliation:
Technical University of Wrocław, Wrocław, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a characterization of the extreme positive contractions on finite dimensional lp-spaces for 1 < p < ∞. This is related to the characterization of the extreme doubly stochastic operators. In Section 2 we present the basic properties of the facial structure of the set of doubly stochastic n × m matrices. In Section 3 we use these facts for description of the facial structure of the set of positive contractions on finite dimensional lp-space. Next is considered stability of the positive part of the unit ball of operators (Section 5). In Section 7 we prove that extreme positive contractions on 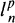are strongly exposed.

1. Terminology and notation. Let (X, 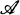, m) be a a-finite measure space. As usual, we denote by LP(m), 1 < p < ∞, the Banach lattice of all p-summable real-valued functions on X with standard norm and order. If X = {1, 2 , …, n) n < ∞, and m is a counting measure we write 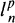instead of LP(m). If X = [0, 1] and m is Lebesgue measure we write briefly LP.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 4 , 01 August 1985 , pp. 682 - 699
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Birkhoff, G. D., Tres obsercaviones sobre et algebra lineal, Univ. Nac. Tucuman Rev. Ser. A. 5 (1946), 147–151.Google Scholar
2. Brualdi, R. A. and Gibson, P. M., Convex polyhedra of doubly stochastic matrices. I. Applications of the permanent function, J. Combinatorial Theory 22 (1977), 194–230.Google Scholar
3. Brualdi, R. A., Combinatorial properties of symmetric non-negative matrices, Colloquio Internazionale sulle Théorie Combinatorie (Roma, 3–15 settembre 1973), Roma, Accademia Nazionale Dei Lincei (1976), 99–120.Google Scholar
4. Gibson, P. M., Faces of faces of transportation poly topes, Proceedings of the Seventh Southeastern Conference On Combinatorics, Graph Theory, And Computing, Louisiana State University, sBaton Rouge, February 9–12 (1976), 323–333.Google Scholar
5. Grzaślewicz, R., Extreme operators on 2-dimensional lp-spaces, Colloq. Math. 44 (1980), 309–315.Google Scholar
6. Grzaślewicz, R., Isometric domain of positive operators on Lp-spaces, to appear in Colloq. Math.Google Scholar
7. Grzaślewicz, R., On extreme infinite doubly stochastic matrices, submitted.CrossRefGoogle Scholar
8. Grzaślewicz, R., Approximation theorems for positive operators in lp, submitted.CrossRefGoogle Scholar
9. Isbel, J. R., Infinite doubly stochastic matrices, Can. Math. Bull. 5 (1962), 1–4.Google Scholar
10. Kendal, M. G., On infinite doubly stochastic matrices and Birkhoff's Problem 111, J. London Math. Soc. 35 (1960), 81–84.Google Scholar
11. Lindenstrauss, J., A remark on extreme doubly stochastic measures, Amer. Math. Monthly 72 (1965), 379–382.Google Scholar
12. Mirsky, L., Result and problems in the theory of doubly stochastic matrices, Z. Wahr. v. Geb. 1 (1963), 319–334.Google Scholar
13. Papadopoulou, S., On the geometry of stable compact convex sets, Math. Ann. 229 (1977), 193–200.Google Scholar
14. Révész, P., A probabilistic solution of problem 111 of G. Birkhoff, Acta Math. Acad. S. Hougaricae 13 (1962), 187–198.Google Scholar