Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-03T13:21:50.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Fermat’s Last Theorem over 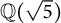$\mathbb {Q}(\sqrt {\text{5}})$ and 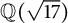$\mathbb {Q}(\sqrt {\text{17}})$

Part of: Diophantine equations Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 November 2022

Imin Chen ,
Aisosa Efemwonkieke  and
David Sun
Imin Chen*
Affiliation:
Department of Mathematics, Simon Fraser University Burnaby, BC V5A 1S6, Canada e-mail: aisosa_efemwonkieke@sfu.ca david_sun_2@sfu.ca
Aisosa Efemwonkieke
Affiliation:
Department of Mathematics, Simon Fraser University Burnaby, BC V5A 1S6, Canada e-mail: aisosa_efemwonkieke@sfu.ca david_sun_2@sfu.ca
David Sun
Affiliation:
Department of Mathematics, Simon Fraser University Burnaby, BC V5A 1S6, Canada e-mail: aisosa_efemwonkieke@sfu.ca david_sun_2@sfu.ca
*
e-mail: ichen@sfu.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove Fermat’s Last Theorem over 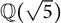$\mathbb {Q}(\sqrt {5})$ and 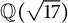$\mathbb {Q}(\sqrt {17})$ for prime exponents 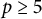$p \ge 5$ in certain congruence classes modulo 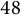$48$ by using a combination of the modular method and Brauer–Manin obstructions explicitly given by quadratic reciprocity constraints. The reciprocity constraint used to treat the case of 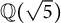$\mathbb {Q}(\sqrt {5})$ is a generalization to a real quadratic base field of the one used by Chen and Siksek. For the case of 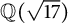$\mathbb {Q}(\sqrt {17})$, this is insufficient, and we generalize a reciprocity constraint of Bennett, Chen, Dahmen, and Yazdani using Hilbert symbols from the rational field to certain real quadratic fields.

Keywords

Fermat equation over quadratic fieldsGalois representationsHilbert modular forms

MSC classification

Primary: 11D41: Higher degree equations; Fermat's equation
Secondary: 11F80: Galois representations 11F03: Modular and automorphic functions
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 1 , February 2024 , pp. 18 - 38
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by an NSERC Discovery Grant (I.C.) and NSERC USRA (A.E.).

References

Bennett, M. A., Chen, I., Dahmen, S. R., and Yazdani, S., Generalized Fermat equations: a miscellany . Int. J. Number Theory 11(2015), no. 1, 1–28.10.1142/S179304211530001XCrossRefGoogle Scholar
Bright, M., Efficient evaluation of the Brauer–Manin obstruction . Math. Proc. Cambridge Philos. Soc. 142(2007), no. 1, 13–23.10.1017/S0305004106009844CrossRefGoogle Scholar
Chen, I., Efemwonkieke, A., and Sun, D., Supporting files for this paper. https://iminchen.org Google Scholar
Chen, I. and Siksek, S., Perfect powers expressible as sums of two cubes . J. Algebra 322(2019), 638–655.10.1016/j.jalgebra.2009.03.010CrossRefGoogle Scholar
Deconinck, H., The generalized Fermat equation over totally real number fields. Ph.D. thesis, University of Warwick, 2016.10.4064/aa8171-1-2016CrossRefGoogle Scholar
Freitas, N., Kraus, A., and Siksek, S., Class field theory, Diophantine analysis and the asymptotic Fermat’s Last Theorem . Adv. Math. 363(2020), Article no. 106964, 37 pp.10.1016/j.aim.2019.106964CrossRefGoogle Scholar
Freitas, N., Kraus, A., and Siksek, S., On asymptotic Fermat over ${\mathbb{Z}}_p$ -extensions of $\mathbb{Q}$ . Algebra Number Theory 14(2020), no. 9, 2571–2574.10.2140/ant.2020.14.2571CrossRefGoogle Scholar
Freitas, N., Kraus, A., and Siksek, S., Local criteria for the unit equation and the asymptotic Fermat’s Last Theorem . Proc. Natl. Acad. Sci. USA 118(2021), no. 12, Article no. 2026449118, 5 pp.CrossRefGoogle Scholar
Freitas, N., LeHung, B. V., and Siksek, S., Elliptic curves over real quadratic fields are modular . Invent. Math. 201(2015), no. 1, 159–206.10.1007/s00222-014-0550-zCrossRefGoogle Scholar
Freitas, N. and Siksek, S., The asymptotic Fermat’s Last Theorem for five-sixths of real quadratic fields . Compos. Math. 151(2015), no. 8, 1395–1415.10.1112/S0010437X14007957CrossRefGoogle Scholar
Freitas, N. and Siksek, S., Fermat’s Last Theorem over some small real quadratic fields . Algebra Number Theory 9(2015), no. 4, 875–895.10.2140/ant.2015.9.875CrossRefGoogle Scholar
Halberstadt, E. and Kraus, A., Courbes de Fermat: résultats et problèmes . J. Reine Angew. Math. 548(2002), 167–234.Google Scholar
Hao, F. H. and Parry, C. J., The Fermat equation over quadratic fields . J. Number Theory 19(1984), no. 1, 115–130.10.1016/0022-314X(84)90096-9CrossRefGoogle Scholar
Ibrahim, M., Modular and reciprocity approaches to a family of Diophantine equations. Ph.D. thesis, University of Warwick, 2009.Google Scholar
Kraus, A., Sur le théorème de Fermat sur $\mathbb{Q}\left(\sqrt{5}\right)$ . Ann. Math. Qué. 39(2015), no. 1, 49–59.10.1007/s40316-015-0030-xCrossRefGoogle Scholar
Mauldin, R. D., A generalization of Fermat’s Last Theorem: the Beal conjecture and prize problem . Notices Amer. Math. Soc. 44(1997), no. 11, 1436–1437.Google Scholar
Neukirch, J., Algebraic number theory, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 322, Springer, Berlin, 1999, translated from the 1992 German original and with a note by Norbert Schappacher, with a foreword by G. Harder.10.1007/978-3-662-03983-0CrossRefGoogle Scholar
Serre, J.-P., A course in arithmetic, Graduate Texts in Mathematics, 7, Springer, New York–Heidelberg, 1973, translated from the French.10.1007/978-1-4684-9884-4CrossRefGoogle Scholar
Taylor, R. and Wiles, A., Ring-theoretic properties of certain Hecke algebras . Ann. of Math. (2) 141(1995), no. 3, 553–572.10.2307/2118560CrossRefGoogle Scholar
The LMFDB Collaboration, The L-functions and modular forms database, 2022. http://www.lmfdb.org.Google Scholar
Voight, J., Quaternion algebras, Graduate Texts in Mathematics, 288, Springer, Cham, 2021.10.1007/978-3-030-56694-4CrossRefGoogle Scholar
Wiles, A., Modular elliptic curves and Fermat’s Last Theorem . Ann. of Math. (2) 141(1995), no. 3, 443–551.CrossRefGoogle Scholar