Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-01T20:17:09.247Z Has data issue: false hasContentIssue false
  • English
  • Français

First Occurrence for the Dual Pairs (U(p, q), U(r, s))

Published online by Cambridge University Press:  20 November 2018

Annegret Paul
Annegret Paul*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720-3840, U.S.A. email: apaul@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a conjecture of Kudla and Rallis about the first occurrence in the theta correspondence, for dual pairs of the form 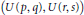$\left( U\left( p,q \right),\,U\left( r,s \right) \right)$ and most representations.

Keywords

22E46
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 636 - 657
Copyright
Copyright © Canadian Mathematical Society 1999

References

[AB] Adams, J. and Barbasch, D., Dual pair correspondence for complex groups. J. Funct. Anal. (1) 132 (1995), 1–42.Google Scholar
[D] Duflo, M., Représentations irréductibles des groupes semi-simples complexes. Lecture Notes in Math. 497, Springer Verlag, 1975.Google Scholar
[H1] Howe, R., _-series and Invariant Theory. In: Proc. Sympos. Pure Math. 33, Amer. Math. Soc., Providence, RI, 1979, 275–285.Google Scholar
[H2] Howe, R., L2-Duality for Stable Dual Pairs. Preprint.Google Scholar
[H3] Howe, R., Transcending classical invariant theory. J. Amer.Math. Soc. (3) 2 (1989), 535–552.Google Scholar
[K] Kudla, S., On the local theta correspondence. Invent.Math. 83 (1986), 229–255.Google Scholar
[Kn] Knapp, A., Representation Theory of Semisimple Groups: An Overview Based on Examples. Princeton University Press, Princeton, 1986.Google Scholar
[KR] Kudla, S. and Rallis, S., First occurrence in the theta correspondence. Notes for a 20 minute talk at the AMS Meeting at Northeastern University, October 8, 1995.Google Scholar
[KV] Knapp, A. and Vogan, D., Cohomological Induction and Unitary Representations. Princeton University Press, Princeton, 1995.Google Scholar
[L1] Li, J.-S., Singular unitary representations of classical groups. Invent.Math. 97 (1989), 237–255.Google Scholar
[L2] Li, J.-S., Local theta lifting for unitary representations with non-zero cohomology. Duke Math. J. 61 (1990), 913–937.Google Scholar
[M] Moeglin, C., Correspondance de Howe pour les paires réductives duales: Quelques calculs dans le cas archimédien. J. Funct. Anal. 85 (1989), 1–85.Google Scholar
[P1] Paul, A., Howe correspondence for real unitary groups. J. Funct. Anal. 159 (1998), 384–431.Google Scholar
[P2] Paul, A., Howe correspondence for real unitary groups II. Proc. Amer.Math. Soc., (to appear).Google Scholar
[Pr] Przebinda, T., The duality correspondence of infinitesimal characters. Colloq. Math. 70 (1996), 93–102.Google Scholar
[R] Ranga Rao, R., On Some Explicit Formulas in the Theory of the Weil Representation. Pacific J. Math. (2) 157 (1993), 335–371.Google Scholar
[Ro] Roberts, Brooks, Tempered representations and the theta correspondence. Canad. J. Math. 50 (1998), 1105–1118.Google Scholar
[SV] Speh, B. and Vogan, D., Reducibility of Generalized Principal Series Representations. ActaMath. 145 (1980), 227–299.Google Scholar
[V1] Vogan, D., Representations of Real Reductive Lie Groups. Birkhäuser, Boston, Basel-Stuttgart, 1981.Google Scholar
[V2] Vogan, D., Unitarizibility of certain series of representations. Ann. of Math. 120 (1984), 141–187.Google Scholar