Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T13:23:04.652Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed Point Theorems for Maps With Local and Pointwise Contraction Properties

Published online by Cambridge University Press:  20 November 2018

Krzysztof Chris Ciesielski  and
Jakub Jasinski
Krzysztof Chris Ciesielski
Affiliation:
Department of Mathematics, West Virginia University, Morgantown, WV 26506-6310 and Department of Radiology, MIPG, University of Pennsylvania, Philadelphia, PA 19104-6021 email: kcies@math.wvu.edu
Jakub Jasinski
Affiliation:
Mathematics Department, University of Scranton, Scranton, PA 18510 email: jakub.jasinski@scranton.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper constitutes a comprehensive study of ten classes of self-maps on metric spaces 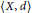$\langle X\,,\,d\rangle $ with the pointwise (i.e., local radial) and local contraction properties. Each of these classes appeared previously in the literature in the context of fixed point theorems.

We begin with an overview of these fixed point results, including concise self contained sketches of their proofs. Then we proceed with a discussion of the relations among the ten classes of self-maps with domains 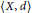$\langle X\,,\,d\rangle $ having various topological properties that often appear in the theory of fixed point theorems: completeness, compactness, (path) connectedness, rectifiable-path connectedness, and $d$-convexity. The bulk of the results presented in this part consists of examples of maps that show non-reversibility of the previously established inclusions between these classes. Among these examples, the most striking is a differentiable auto-homeomorphism 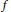$f$ of a compact perfect subset 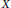$X$ of 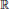$\mathbb{R}$ with 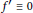${{f}^{'}}\,\equiv \,0$, which constitutes also a minimal dynamical system. We finish by discussing a few remaining open problems on whether the maps with specific pointwise contraction properties must have the fixed points.

Keywords

54H25, 37C25fixed pointperiodic pointcontractive maplocally contractive mappointwise contractive mapradially contractive maprectifiable-path connected spaced-convexgeodesicremetrizationcontraction mapping principle
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 3 , 01 June 2018 , pp. 538 - 594
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Acosta, D. and Lawson, T., Weak contractions and fixed points. College Math. J. no. 1, 35–41. http://dx.doi.org/10.4169/college.math.j.46.1.35 Google Scholar
[2] Alghamdi, M. A., Kirk, W. A., and Shahzad, N., Locally nonexpansive mappings in geodesic and length spaces. Topology Appl. 173(2014), 59–73 http://dx.doi.org/10.1016/j.topol.2014.04.020Google Scholar
[3] Almezel, S., Ansari, Q. H., and Khamsi, M. A., eds., Topics in fixed point theory. Springer, Cham. Switzerland, 2014. http://dx.doi.org/10.1007/978-3-319-01586-6 Google Scholar
[4] Banach, S., Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fund. Math. 3(1922), 133–181.Google Scholar
[5] Binh, T. Q., Some results on locally contractive mappings. Nonlinear Funct. Anal. Appl. 11(2006), no. 3, 371–383.Google Scholar
[6] Bruckner, A. M., Bruckner, J. B., and Thomson, B. S., Real analysis. Prentice-Hall, New Jersey 1997.Google Scholar
[7] Carl, S. and Heikkilä, S., Fixed point theory in ordered sets and applications. Springer, New York, 2011.Google Scholar
[8] Ciesielski, K. C. and Jasinski, J., Smooth Peano functions for perfect subsets of the real line. Real Anal. Exchange 39(2014), no. 1, 57–72.Google Scholar
[9] Ciesielski, K. C. and Jasinski, J., On closed subsets of R and of R2 admitting Peano functions. Real Anal. Exchange 40(2015), no. 2, 309–317.Google Scholar
[10] Ciesielski, K. C. and Jasinski, J., An auto-homeomorphism of a Cantor set with derivative zero everywhere. J. Math. Anal. Appl. 434(2016), no. 2, 1267–1280. http://dx.doi.org/10.1016/j.jmaa.2015.09.076 Google Scholar
[11] Ciesielski, K. C. and Jasinski, J., On fixed points of locally and pointwise contracting maps. Topology Appl. 204(2016), 70–78. http://dx.doi.org/10.1016/j.topol.2016.02.011 Google Scholar
[12] Clarke, F. H., Pointwise contraction criteria for the existence of fixed points. Canad. Math. Bull. 21(1978), no. 1, 7–11. http://dx.doi.org/10.4153/CMB-1978-002-8 Google Scholar
[13] Daffer, P. Z. and Kaneko, H., A new proof of a fixed point theorem of Edelstein. Sci. Math. 1(1998), 97–101.Google Scholar
[14] Ding, C. and Nadler, S. B., The periodic points and the invariant set of an ε-contractive map. Appl. Math. Lett. 15(2002), no. 7, 793–801. http://dx.doi.org/10.1016/S0893-9659(02)00044-7 Google Scholar
[15] Edelstein, M., An extension of Banach's contraction principle. Proc. Amer. Math. Soc. 12(1961), 7–10. http://dx.doi.org/10.2307/2034113 Google Scholar
[16] Edelstein, M., On fixed and periodic points under contractive mappings. J. London Math. Soc. 37(1962), 74–79. http://dx.doi.org/10.1112/jlms/s1-37.1.74 Google Scholar
[17] Engelking, R., General topology. Heldermann Verlag, Berlin.Google Scholar
[18] Espínola, R., Kim, E. S., and Kirk, W. A., Fixed point properties of mappings satisfying local contractive conditions. Nonlinear Anal. Forum 6(2001), no. 1, 103–111.Google Scholar
[19] Granas, A. and Dugundji, J., Fixed point theory. Springer-Verlag, New York, 2003. http://dx.doi.org/10.1007/978-0-387-21593-8 Google Scholar
[20] Holmes, R. D., Fixed points for local radial contractions. Proc. Sem., Dalhousie Univ., Halifax, NS, 1975, Academic Press, New York, 1976, pp. 79–89.Google Scholar
[21] Hu, T. and Kirk, W. A., Local contractions in metric spaces. Proc. Amer. Math. Soc. 68(1978), 121–124. http://dx.doi.org/10.1090/S0002-9939-1978-0464180-2 Google Scholar
[22] Jungck, G., Local radial contractions—a counter example. Houst. J. Math. 8(1982), 501–506.Google Scholar
[23] Kirk, W. A., Contracting mappings and extensions. In: Handbook of metric fixed point theory. Kluwer, Dordrecht, 2001, pp. 1–34.Google Scholar
[24] Kirk, W. A. and Shahzad, N., Fixed point theory in distance spaces. Springer, Cham, Switzerland, 2014.Google Scholar
[25] Marjanović, M. M., Fixed points of local contractions. Publ. Inst. Math. 20(34)(1976), 185–190.Google Scholar
[26] Menger, K., Untersuchungen über allgemeine Metrik. Math. Ann. 103(1930), no. 1, 466–501. http://dx.doi.org/10.1007/BF01455705 Google Scholar
[27] Munkres, J. R., Topology. Second ed. Prentice Hall, New Jersey, 2000.Google Scholar
[28] Mycielski, J., On the existence of a shortest arc between two points of a metric space. Houston J. Math. 20(1994), no. 3, 491–494.Google Scholar
[29] Myers, S. B., Arcs and geodesics in metric spaces. Trans. Amer. Math. Soc. 57(1945), no. 2, 217–227. http://dx.doi.org/10.1090/S0002-9947-1945-0011792-9 Google Scholar
[30] Rakotch, E., A note on α-locally contractive mappings. Bull. Res. Council Israel 40(1962), 188–191.Google Scholar
[31] Rhoades, B. E., A comparison of various definitions of contractive mappings. Trans. Amer. Math. Soc. 226(1977), 257–290. http://dx.doi.org/10.1090/S0002-9947-1977-0433430-4 Google Scholar
[32] Rosenholtz, I., Evidence of a conspiracy among fixed point theorems. Proc. Amer. Math. Soc. 53(1975), 213–218. http://dx.doi.org/10.1090/S0002-9939-1975-0400201-8 Google Scholar