Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-01T20:54:14.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuation of Matrix Entries and Application to Outliers of Elliptic Matrices

Published online by Cambridge University Press:  20 November 2018

Florent Benaych-Georges ,
Guillaume Cébron  and
Jean Rochet
Florent Benaych-Georges
Affiliation:
Université Paris Descartes, 45, rue des Saints-Péres 75270 Paris Cedex 06, France e-mail: florent.benaych-georges@parisdescartes.fr
Guillaume Cébron
Affiliation:
IMT, Université Paul Sabatier, 118 Route de Narbonne 31062 Toulouse Cedex 04, France e-mail: guillaume.cebron@math.univ-toulouse.fr
Jean Rochet
Affiliation:
Université Paris Descartes, 45, rue des Saints-Péres 75270 Paris Cedex 06, France e-mail: jean.rochet@parisdescartes.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any family of 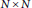$N\,\times \,N$ random matrices 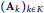${{\left( {{\text{A}}_{k}} \right)}_{k\in K}}$ that is invariant, in law, under unitary conjugation, we give general sufficient conditions for central limit theorems for random variables of the type 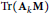$\text{Tr}\left( {{\text{A}}_{k}}\text{M} \right)$, where the matrix 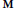$\text{M}$ is deterministic (such random variables include, for example, the normalized matrix entries of 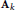${{\text{A}}_{k}}$). A consequence is the asymptotic independence of the projection of the matrices 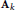${{\text{A}}_{k}}$ onto the subspace of null trace matrices from their projections onto the orthogonal of this subspace. These results are used to study the asymptotic behavior of the outliers of a spiked elliptic random matrix. More precisely, we show that the fluctuations of these outliers around their limits can have various rates of convergence, depending on the Jordan Canonical Form of the additive perturbation. Also, some correlations can arise between outliers at a macroscopic distance from each other.These phenomena have already been observed with random matrices from the Single Ring Theorem.

Keywords

60B2015B5260F0546L54random matrixGaussian fluctuationspiked modelelliptic random matrixWeingarten calculusHaar measure
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 3 - 25
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Anderson, G., Guionnet, A., and Zeitouni, O., An introduction to random matrices. Cambridge Studies in Advanced Aathematics, 118. Cambridge University Press, Cambridge, 2010.Google Scholar
[2] D'Aristotile, A., Diaconis, P., and Newman, C., Brownian motion and the classical groups. In: Probability, statisitica and their applications: Papers in Honor of Rabii Bhattacharaya. K. Athreya et al. eds. IMS Lecture Notes Monogr. Ser., 41. Institute of Mathematical Statistics,Beechwood, OH, 2003, pp. 97–116.http://dx.doi.org/10.1214/lnms/121509160 Google Scholar
[3] Arratia, R., and Tavare, S., The cycle structure of random permutations. Ann. Probab. 20(1992), no. 3, 1567–1591. http://dx.doi.Org/10.1214/aop/1176989707 Google Scholar
[4] Bai, Z. D. and Silverstein, J. W., Spectral analysis of large dimensional random matrices. Second edition, Springer, New York, 2009. http://dx.doi.Org/10.1007/978-1-4419-0661-8 Google Scholar
[5] Bai, Z. D. and Yao, J. E, On the convergence of the spectral empirical process of Wigner matrices. Bernoulli 11(2005), no. 6 , 1059–1092. http://dx.doi.org/10.3150/bjV1137421640Google Scholar
[6] Baik, J., Ben Arous, G., and Péché, S., Phase transition of the largest eigenvalue for nonnull complex sample covariance matrices. Ann. Probab. 33(2005), no. 5,1643–1697.http://dx.doi.org/10.1214/009117905000000233 Google Scholar
[7] Benaych-Georges, F., Central limit theorems for the Brownian motion on large unitary groups. Bull. Soc. Math. France 139(2011), no. 4, 593–610.http://dx.doi.org/10.24033/bsmf.2621 Google Scholar
[8] Benaych-Georges, F., A. Guionnet, and M. Maida, Fluctuations of the extreme eigenvalues of finite rank deformations of random matrices. Electron. J. Prob. 16(2011), no. 60,1621–1662.http://dx.doi.org/10.1214/EJP.v16-929 Google Scholar
[9] Benaych-Georges, F., Large deviations of the extreme eigenvalues of random deformations of matrices. Probab. Theory Related Fields 154(2012), no. 3, 703–751.http://dx.doi.Org/10.1007/s00440-011-0382-3 Google Scholar
[10] Benaych-Georges, F. and Rao, R. N., The eigenvalues and eigenvectors of finite, low rank perturbations of large random matrices. Adv. Math. 227(2011), no. 1, 494–521. http://dx.doi.Org/10.1016/j.aim.2011.02.007 Google Scholar
[11] Benaych-Georges, F., The singular values and vectors of low rank perturbations of large rectangular random matrices. J. Multivariate Anal. 111(2012), 120–135.http://dx.doi.Org/10.1016/j.jmva.2O12.04.019 Google Scholar
[12] Benaych-Georges, F. and Rochet, J., Outliers in the single ring theorem. Probab. Theory Related Fields 165(2016), no. 1, 313–363.http://dx.doi.Org/10.1007/s00440-01 5-0632-x Google Scholar
[13] Benaych-Georges, F., Fluctuations for analytic test functions in the single ring theorem. To appear in Indiana Univ. Math. J. Google Scholar
[14] Bordenave, C. and Capitaine, M., Outlier eigenvalues for deformed i.i.d. random matrices. Comm. Pure Appl. Math. 69(2016), no. 11, 2131–2194. http://dx.doi.Org/10.1002/cpa.21629 Google Scholar
[15] Borel, É. Sur les principes de la théorie cinétique des gaz. Ann. Sci.École Norm. Sup. 23(1906), 9–32. http://dx.doi.Org/10.24033/asens.561 Google Scholar
[16] Capitaine, M., Donati-Martin, C., and Féral, D., The largest eigenvalue of finite rank deformation of large Wigner matrices: convergence and non universality of the fluctuations. Ann. Probab. 37(2009), no. 1, 1–47.http://dx.doi.org/10.1214/08-AOP394 Google Scholar
[17] Capitaine, M., Central limit theorems for eigenvalues of deformations of Wigner matrices. Ann. Inst. Henri Poincaré Probab. Stat. 48(2012), no. 1,107–133.http://dx.doi.org/10.1214/10-AIHP410 Google Scholar
[18] Capitaine, M., Donati-Martin, C., Féral, D., and Février, M., Free convolution with a semi-circular distribution and eigenvalues of spiked deformations of Wigner matrices. Elec. J. Probab. 16(2011), no. 64,1750–1792. http://dx.doi.org/10.1214/EJP.v16-934 Google Scholar
[19] Cébron, G. and Kemp, T., Fluctuations of Brownian motions on . To appear in Ann. Inst.Henri Poincaré Probab. Stat. arxiv:1409.5624 Google Scholar
[20] Chafaï, D., Circular law for noncentral random matrices. J. Theoret. Probab. 23(2010), no. 4, 945–950.http://dx.doi.Org/10.1007/s10959-010-0285-8 Google Scholar
[21] Chatterje, S. and Meckes, E., Multivariate normal approximation using exchangeable pairs. ALEA Lat. Am. J. Probab. math. Stat. 4(2008), 257–283.Google Scholar
[22] Collins, B., Moments and cumulants of polynomial random variables on unitary groups, the Itzykson-Zuber integral, and free probability. Int. Math. Res. Not. (2003), no. 17, 953–982.Google Scholar
[23] Collins, B., Mingo, J. A., Sniady, P., and Speicher, R., Second order freeness and fluctuations of random matrices. III. Higher order freeness and free cumulants. Doc. Math. 12(2007), 1–70.Google Scholar
[24] Collins, B. and Sniady, P., Integration with respect to the Hoar measure on unitary, orthogonal and symplectic group. Comm. Math. Phys. 264(2008), no. 3, 773–795.http://dx.doi.org/10.1007/s00220-006-1554-3 Google Scholar
[25] Collins, B. and Stolz, M., Borel theorems for random matrices from the classical compact symmetric spaces. Ann. Probab. 36(2008), no. 3, 876–895. http://dx.doi.Org/10.1214/07-AOP341 Google Scholar
[26] Diaconis, P. and Shahshahan, M., On the eigenvalues of random matrices. J. Appl. Probab. 31A(1994), 49–62.http://dx.doi.org/10.2307/3214948 Google Scholar
[27] Féral, D. and Péché, S., The largest eigenvalue of rank one deformation of large Wigner matrices. Comm. Math. Phys. 272(2007), 185–228. http://dx.doi.Org/10.1007/s00220-007-0209-3 Google Scholar
[28] Jiang, T., How many entries of a typical orthogonal matrix can be approximated by independent normals? Ann. Probab. 34(2006), no. 4,1497–1529.http://dx.doi.Org/10.1214/009117906000000205 Google Scholar
[29] Johansson, K., On the fluctuations of eigenvalues of random Hermitian matrices. Duke Math. J. 91(1998), 151–204.http://dx.doi.org/10.1215/S0012-7094-98-09108-6 Google Scholar
[30] Johnstone, I. M., On the distribution of the largest eigenvalue in principal components analysis. Annals of Stat. 29(2001), no. 2, 295–327. http://dx.doi.org/10.1214/aos/1009210544 Google Scholar
[31] Knowles, A. and Yin, J., The isotropic semicircle law and deformation of Wigner matrices. Comm. Pure Appl. Math. 66, no. 11,1663–1750, 2013.http://dx.doi.org/10.1002/cpa.21450 Google Scholar
[32] Knowles, A. and Yin, J., The outliers of a deformed Wigner matrix, Ann. Probab. 42(2014), no. 5, 1980–2031.http://dx.doi.Org/10.1214/13-AOP855 Google Scholar
[33] Levy, T. and Maïda, M., Central limit theorem for the heat kernel measure on the unitary group. J. Funct. Anal. 259(2010), no. 12, 3163–3204.http://dx.doi.Org/10.1016/j.jfa.201 0.08.005 Google Scholar
[34] Meckes, E., Linear functions on the classical matrix groups. Trans. Amer. Math. Soc. 360(2008), no. 10, 5355–5366.http://dx.doi.org/10.1090/S0002-9947-08-04444-9 Google Scholar
[35] Mingo, J. A. and Nica, A., Annular noncrossing permutations and partitions, and second-order asymptotics for random matrices. Int. Math. Res. Not. (2004), no. 28,1413–1460,Google Scholar
[36] Mingo, J. A., Sniady, P., and Speicher, R., Second order freeness and fluctuations of random matrices. II. Unitary random matrices. Adv. Math. 209(2007), no. 1, 212–240. http://dx.doi.Org/10.1016/j.aim.2006.05.003 Google Scholar
[37] Mingo, J. A. and Speicher, R., Second order freeness and fluctuations of random matrices. I. Gaussian and Wishart matrices and cyclic Fock spaces. J. Funct. Anal. 235(2006), no. 1, 226–270.http://dx.doi.Org/10.1016/j.jfa.2005.10.007 Google Scholar
[38] Naumov, A., Elliptic law for real random matrices. Vestnik Moskov. Univ. Ser. XV Vychisl. Mat. Kibernet. (2013), no. 1, 31–38, 48.Google Scholar
[39] Nguyen, H. and O‚Rourke, S., The elliptic law. Int. Math. Res. Not. IMRN, (2015), no. 17, 7620–7689.Google Scholar
[40] Nica, A. and Speicher, R., Lectures on the combinatorics of free probability. London Mathematical Society Lecture Note Series, 335. Cambridge University Press, Cambridge, 2006.Google Scholar
[41] Rajagopalan, A.B., Outlier eigenvalue fluctuations of perturbed iid matrices. Proquest, Ann Arbor, MI, 2015.Google Scholar
[42] Rains, E., Normal limit theorems for symmetric random matrices. Probab. Theory Relat. Fields 112(1998), 411–423. http://dx.doi.Org/10.1007/s0044000501 95 Google Scholar
[43] Rider, B. and Silverstein, J. W., Gaussian fluctuations for non-Hermitian random matrix ensembles. Ann. Probab. 34(2006), no. 6, 2118–2143.http://dx.doi.Org/10.1214/00911 7906000000403 Google Scholar
[44] Rochet, J., Complex outliers of Hermitian random matrices. J. Theor. Probab. (2016). https://doi.org/10.1007/sl0959-016-0686-4 Google Scholar
[45] O‚Rourke, S. and Matchett Wood, P., Spectra of nearly Hermitian random matrices. Annal. Inst. Henri Poincaré 52(2016), no. 4, 1877–1896.http://dx.doi.Org/10.1214/15-AIHP702 Google Scholar
[46] O‚Rourke, S. and Renfrew, D., Low rank perturbations of large elliptic random matrices. Electron. J. Probab. 19(2014), 43, 65.Google Scholar
[47] O‚Rourke, S. Central limit theorem for linear eigenvalue statistics of elliptic random matrices. J. Theoret. Probab. 29(2016), no. 3,1121–1191.http://dx.doi.Org/10.1007/s10959-015-0609-9 Google Scholar
[48] Péché, S., The largest eigenvalue of small rank perturbations of Hermitian random matrices. Prob. Theory Relat. Fields 134(2006), no. 1,127–173. http://dx.doi.Org/10.1007/s00440-005-0466-z Google Scholar
[49] Pizzo, A., Renfrew, D., and Soshnikov, A., On finite rank deformations of Wigner matrices, Ann. Inst. Henri Poincaré Probab. Stat. 49(2013), no. 1, 64–94.http://dx.doi.Org/10.1214/11-AIHP459 Google Scholar
[50] Sommers, H.-J., Crisanti, A., Sompolinsky, H., and Stein, Y., Spectrum of large random asymmetric matrices. Phys. Rev. Lett. 60(1988), 1895–1899.http://dx.doi.Org/10.1103/PhysRevLett.60.1895 Google Scholar
[51] Tao, T., Outliers in the spectrum of iid matrices with bounded rank perturbations. Probab. Theory Related Fields 155(2013), 231–263. http://dx.doi.Org/10.1007/s00440-011-0397-9 Google Scholar
[52] Tsou, B., The distribution of permutation matrix entries under randomized basis. arxiv:1 509.06505 Google Scholar