Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-08T14:28:39.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Framed Stratified Sets in Morse Theory

Published online by Cambridge University Press:  20 November 2018

André Lebel
André Lebel*
Affiliation:
Champlain-St.Lawrence College Québec
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we present a smooth framework for some aspects of the “geometry of CW complexes”, in the sense of Buoncristiano, Rourke and Sanderson. We then apply these ideas to Morse theory, in order to generalize results of Franks and Iriye-Kono.

More precisely, consider a Morse function 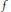$f$ on a closed manifold 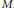$M$. We investigate the relations between the attaching maps in a 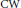$\text{CW}$ complex determined by 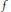$f$, and the moduli spaces of gradient flow lines of 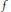$f$, with respect to some Riemannian metric on 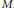$M$.

Keywords

57R7057N8055N45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 396 - 416
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Austin, D. M. and Braam, P. J., Morse-Bott theory and equivariant cohomology. Preprint, 1994.Google Scholar
[2] Buoncristiano, S. and Dedo, M., Local blow-up of stratified sets up to bordism. Trans. Amer. Math. Soc. 273 (1982), 253–280.Google Scholar
[3] Buoncristiano, S., Rourke, C. P. and Sanderson, B. J., A geometric approach to homology theory. Cambridge University Press, 1976.Google Scholar
[4] Cohen, R. L., Jones, J. D. S. and Segal, G. B., Morse theory and classifying spaces. Preprint, 1992.Google Scholar
[5] Franks, J., Morse-Smale flows and homotopy theory. Topology 18 (1979), 199–215.Google Scholar
[6] Goresky, M., Whitney stratified chains and cochains. Trans. Amer. Math. Soc. 267 (1981), 175–196.Google Scholar
[7] Hirsch, M., Differential Topology. Springer, 1976.Google Scholar
[8] Iriye, K. and Kono, A., Morse function and attaching map. J. Math. Kyoto Univ. (1) 35 (1995), 79–83.Google Scholar
[9] Lebel, A., Framed stratified sets in Morse theory. Ph.D. thesis, University of Warwick, 1996.Google Scholar
[10] Schwartz, M., Morse Homology. Birkhauser, 1993.Google Scholar
[11] Smale, S., On gradient dynamical systems. Ann. of Maths. 74 (1961), 199–206.Google Scholar
[12] Verona, A., Stratified mappings—Structure and Triangulability. Lecture Notes in Math. 1102, Springer-Verlag, 1984.Google Scholar