Online ordering is currently unavailable due to technical issues. We apologise for any delays responding to customers while we resolve this. For further updates please visit our website: https://www.cambridge.org/news-and-insights/technical-incident Due to planned maintenance there will be periods of time where the website may be unavailable. We apologise for any inconvenience.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 November 2018
In a recent paper (3)* the following theorem was proved for real matrices.
Theorem 1. If A is a symmetric matrix and Q is a skew-symmetric matrix such that A + Q is non-singular, then
1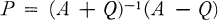
is a cogredient automorph (c.a.) of A whose determinant is + 1 and having theproperty that A and I + P span the same row space.
Conversely, if P is a c.a. of A whose determinant is + 1 and if P has theproperty that I + P and A span the same row space, then there exists a skew symmetricmatrix Q such that P is given by equation (1).
Theorem 1 reduces to the well-known Cayley parameterization in the case where A is non-singular. A similar and somewhat simpler result (Theorem 4) was given for the case when the underlying field is the complex field. It was also shown that the second part of the theorem (in either form) is false when the characteristic of the underlying field is 2. The purpose of this paper is to simplify the proof of Theorem 1 and at the same time, to extend these results to matrices over an arbitrary field of characteristic ≠ 2.
You have
Access
