Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-09T02:20:11.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Actions on Flag Manifolds and Cobordism

Published online by Cambridge University Press:  20 November 2018

P. Sankaran  and
K. Varadarajan
P. Sankaran
Affiliation:
School of Mathematics, SPIC Science Foundation, 92 G.N. Chetty Road, T. Nagar, Madras 600017, India
K. Varadarajan
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, T2N 1N4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we show that any 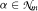(respectively α є Ωm) can be represented by a closed smooth (respectively closed, oriented smooth) manifold Mm admitting a smooth (Z/2)m (respectively S1)-action with a finite stationary set. We also completely determine the Grassman manifolds 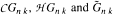which are oriented boundaries as well as those which represent non-torsion elements in Ω*.

Keywords

57R7557R85(Oriented) cobordismstationary setPontrjagin numbers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 45 , Issue 3 , 01 June 1993 , pp. 650 - 661
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Adams, J. F., Lectures on Lie Groups, University of Chicago Press, Midway Reprint, (1982).Google Scholar
2. Borel, A., La cohomologie mod2 de certains espaces homogènes, Comm. Math. Helv. 27(1953), 165— 197.Google Scholar
3. Borel, A., Sur la cohomologie des espaces fibres principaux et des expaces homogènes de groupe de Lie compacts, Ann. Math. 57(1953), 115–207.Google Scholar
4. Borel, A. and Hirzebruch, F., Characteristic classes and homogeneous spaces, Amer. J. Math. 80(1958), 458–535.Google Scholar
5. Chern, S. S., Hirzebruch, F., and J.-R Serre, The index of a fibered manifold, Proc. Amer. Math. Soc. 8(1957), 587–596.Google Scholar
6. Conner, P. E., Differentiable periodic maps, 2nd Ed., L.N.M. (738), Springer-Verlag, 1979.Google Scholar
7. Conner, P. E. and Floyd, E. E., Differentiable periodic maps, Ergebnisse Sr-33, Springer-Verlag, 1964.Google Scholar
8. Floyd, E. E., Stiefel-Whitney numbers of quaternionic and related manifolds, Trans. Amer. Math. Soc. 155(1971), 77–94.Google Scholar
9. Hsiang, W.-C. and Szczarba, R. H., On the tangent bundle for the Grassmann manifold, Amer. J. Math. 86(1964), 698–704.Google Scholar
10. Husemoller, D., Fibre bundles, G.T.M.(20), Springer-Verlag, 1985.Google Scholar
11. Kobayashi, S. and Nomizu, K., Foundations of differential geometry Vol. II, Interscience Publishers, 1969.Google Scholar
12. Korbas, J., Vector fields on real flag manifolds, Ann. Glob. Anal. Geom. 3(1985), 173–184.Google Scholar
13. Lam, K. Y., A formula for the tangent bundle of flag manifolds and related manifolds, Trans. Amer. Math. Soc. 213(1975), 305–314.Google Scholar
14. Milnor, J. W., On the cobordism ring Ω* and a complex analogue, Amer. J. Math. 82(1960), 505–521.Google Scholar
15. Milnor, J. W. and Stasheff, J. D., Characteristic classes, Ann. Math. Stud. 76, Princeton, (1974).Google Scholar
16. Mong, S., The index of complex and quaternionic Grassmannians via Lefschetz formula, Adv. Math. 15(1975), 169–174.Google Scholar
17. Sankaran, P., Cobordism of flag manifolds, Institute of Mathematical Sciences, Madras, India, (1987), preprint.Google Scholar
18. Sankaran, P., Determination of Grassmann manifolds which are boundaries, Canad. Math. Bull. 34(1991), 119–122.Google Scholar
19. Sankaran, P., Which Grassmannians bound?, Arch. Math. 50(1988), 474–476 Google Scholar
20. Shanahan, P., On the signature ofGrassmannians, Pac. J. Math. 84(1979), 483–490.Google Scholar
21. Stewart, B. M., Theory of numbers, 2nd Ed. Macmillan & Co., New York, 1964.Google Scholar
22. Stong, R. E., Equivariant bordism and (Z2)K actions, Duke. Math. J. 37(1970), 779–785.Google Scholar
23. Stong, R. E., Stationary point free group actions, Proc. Am. Math. Soc. 18(1967), 1089–1092.Google Scholar
24. Stong, R. E., Notes on cobordism theory, Mathematical Notes, Princeton Univ. Press, (1968).Google Scholar
25. Stong, R. E., Math. Reviews, 89d:57050.Google Scholar