Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-01T20:43:11.271Z Has data issue: false hasContentIssue false
  • English
  • Français

Growth and Zeros of the Zeta Function for Hyperbolic Rational Maps

Published online by Cambridge University Press:  20 November 2018

Hans Christianson
Hans Christianson*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, U.S.A. email: hans@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper describes new results on the growth and zeros of the Ruelle zeta function for the Julia set of a hyperbolic rational map. It is shown that the zeta function is bounded by exp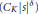$({{C}_{k}}{{\left| s \right|}^{\delta }})$ in strips 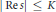$|\,\text{Re}\,s\,|\,\le \,K$, where $\delta$ is the dimension of the Julia set. This leads to bounds on the number of zeros in strips (interpreted as the Pollicott–Ruelle resonances of this dynamical system). An upper bound on the number of zeros in polynomial regions 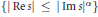$\left\{ \left| \,\operatorname{Re}s \right|\,\le \,{{\left| \,\operatorname{Im}s \right|}^{\alpha }} \right\}$ is given, followed by weaker lower bound estimates in strips 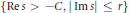$\{\text{Re}\,s\,>\,-C,\,|\,\text{IM}\,s|\,\le \,r\}$, and logarithmic neighbourhoods 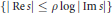$\{|\text{Re}s|\le {{}_{\rho }}\log |\operatorname{Im}s|\}$. Recent numerical work of Strain-Zworski suggests the upper bounds in strips are optimal.

Keywords

37C30zeta functiontransfer operatorcomplex dynamics
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 2 , 01 April 2007 , pp. 311 - 331
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Ahlfors, L., Möbius Transformations in Several Dimensions. University of Minnesota, School of Mathematics, Minneapolis, MN, 1981.Google Scholar
[2] Atiyah, M. F. and Bott, R., A Lefschetz fixed point formula for elliptic complexes. I. Ann. of Math. 86(1967), 374–407.Google Scholar
[3] Carleson, L., and Gamelin, T.. Complex Dynamics. Springer-Verlag, New York, 1993.Google Scholar
[4] Falconer, K., Fractal Geometry, Mathematical Foundations and Applications. John Wiley, Chichester, 1990.Google Scholar
[5] Falconer, K., Techniques in Fractal Geometry. John Wiley, Chichester, 1997.Google Scholar
[6] Goldman, W., Complex Hyperbolic Geometry. Oxford University Press, Oxford, 1999.Google Scholar
[7] Guillopé, L., Lin, K., and Zworksi, M., The Selberg function for convex co-compact Schottky groups. Comm. Math. Phys. 245(2004), no. 1, 149–176.Google Scholar
[8] Guillopé, L., Lin, K., and Zworksi, M., The wave trace for Riemann surfaces. Geom. Funct. Anal. 9(1999), no. 6, 1156–1168.Google Scholar
[9] Hörmander, L., The Analysis of Linear Partial Differential Operators. I. Grundlehren der Mathematischen Wissenschaften 256, Springer-Verlag, Berlin, 1983.Google Scholar
[10] Jenkinson, O., and Pollicott, M., Calculating Hausdorff dimension of Julia sets and Kleinian limit sets. Amer. J. Math. 124(2002), no. 3, 495–545.Google Scholar
[11] McMullen, C., Hausdorff dimension and conformal dynamics. II. Geometrically finite rational maps. Comment. Math. Helv. 75(2000), no. 4, 535–593.Google Scholar
[12] Ruelle, D., Dynamical zeta functions and transfer operators. Notices Amer. Math. Soc. 49(2002), no. 8, 887–895.Google Scholar
[13] Ruelle, D., Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34(1976), no. 3, 231–242.Google Scholar
[14] Simon, B., Trace Ideals and Their Applications. London Mathematical Society Lecture Note Series 35. Cambridge University Press, Cambridge. 1979.Google Scholar
[15] Sjöstrand, J., and Zworski, M., Lower bounds on the number of scattering poles. Comm. Partial Differential Equations 18(1993), no. 5-6, 847–857.Google Scholar
[16] Strain, J. and Zworski, M., Growth of the zeta function for a quadratic map and the dimension of the Julia set. Nonlinearity 17(2004), no. 5, 1607–1622.Google Scholar
[17] Urbański, M., Measures and dimensions in conformal dynamics. Bull. Amer. Math. Soc. 40(2003), no. 3, 281–321.Google Scholar
[18] Zworski, M., Dimension of the limit set and the density of resonances for convex co-compact hyperbolic surfaces. Invent. Math. 136(1999), no. 2, 353–409.Google Scholar
[19] Zworski, M., Resonances in physics and geometry. Notices Amer. Math. Soc. 46(1999), no. 3, 319–328.Google Scholar