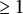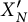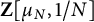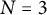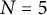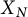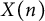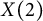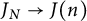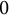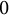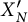1 Introduction
Let
$\Gamma $
be a subgroup of finite index of
${\mathrm {SL}}_2({\mathbb {Z}})$
. This subgroup acts by homographies on the complex upper half-plane
$\mathfrak {H}$
. Consider the corresponding modular curve
${Y_\Gamma =\Gamma \backslash \mathfrak {H}}$
, and its compactification obtained by adding the cusps
$X_\Gamma $
. We say that
$X_\Gamma $
satisfies the Manin–Drinfeld principle if any cuspidal (i.e., supported on the cusps) divisor of degree
$0$
is torsion in the Jacobian of
$X_\Gamma $
. Manin and Drinfeld proved that it is the case when
$\Gamma $
is a congruence subgroup.
For a subgroup of finite index (not necessarily a congruence subgroup), K. Murty and Ramakrishnan [Reference Murty and Ramakrishnan13] give an analytic criterion for the Manin–Drinfeld principle to be satisfied. As an illustrative example, Murty and Ramakrishnan consider modular curves attached to certain subgroups of
$\Gamma (2)$
: Fermat curves, and what they propose to call Heisenberg curves. We revisit those examples. In [Reference Banerjee and Merel2], we reconsider this question and give an analytic criterion of a different nature, but also based on Eisenstein series; this is unconnected to the present work, which is purely algebraic in nature.
The Heisenberg curves are defined as follows from the complex analytic point of view. Let A and B be the classes of the matrices
$\begin {pmatrix} 1 & 2 \\ 0 & 1 \\ \end {pmatrix}$
and
$\begin {pmatrix} 1 & 0 \\ 2 & 1 \\ \end {pmatrix}$
, respectively, in
${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
. These matrices generate freely the group
${\bar \Gamma }(2)$
. Let
$C=ABA^{-1}B^{-1}$
.
Let N be an integer
$>0$
. Denote by
$\Phi _N$
the kernel of the morphism
${{\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2}$
which to A associates
$(1,0)$
and to B associates
$(0,1)$
. The corresponding modular curve is the Fermat modular curve and is denoted by
$X_{N}$
. It can be identified with the complex points of the Fermat curve
$F_N$
(see, for instance, [Reference Lang7, Reference Rohrlich17]). Let
$\Phi _N'$
be the subgroup of
$\Phi _N$
generated by
$A^N$
,
$B^N$
,
$C^N$
and the third term
$[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
in the descending central series of
${\bar \Gamma }(2)$
. An exact sequence of groups follows:
$$ \begin{align*}1\rightarrow \Phi_N'\rightarrow {\bar\Gamma}(2)\rightarrow H_N\rightarrow 1, \end{align*} $$
where
$H_N$
is a central extension of
$({{\mathbb {Z}}/N{\mathbb {Z}}})^{2}$
by
${{\mathbb {Z}}/N{\mathbb {Z}}}$
(coinciding with the
${\mathbb {Z}}/N{\mathbb {Z}}$
-points of the Heisenberg group). The Nth Heisenberg modular curve, in the sense of Murty and Ramakrishnan, is
$X^{\prime }_N=X_{\Phi ^{\prime }_N}$
.
Let
$\mathbb {Q}(\mu _{N})$
be a cyclotomic extension of
$\mathbb {Q}$
generated by Nth roots of unity. Denote by
${\mathbb {Z}}[\mu _{N}]$
its ring of integers. The covering
$X^{\prime }_{N}\rightarrow X_{N}$
extends to a morphism
$F^{\prime }_{N}\rightarrow F_{N}$
of curves over
$\mathbb {Q}(\mu _{N})$
that we call the Heisenberg covering of the Fermat curve.
Theorem 1.1 Suppose N is an odd integer. The Heisenberg modular curve
$X^{\prime }_N$
extends to a smooth projective scheme
${\mathcal {F}}^{\prime }_N$
of relative dimension one over
$\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
given by the following model:
$$ \begin{align*}X^{N}+Y^{N}=Z^{N} \end{align*} $$
and, for every primitive Nth root of unity
$\zeta $
in
$\mathbb {Q}(\mu _{N})$
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j}Z)^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j}Z)^{j}U_{\zeta}^{N}. \end{align*} $$
It seems to have been known to Deligne (see a comment in [Reference Murty and Ramakrishnan13]) that the generic fiber
$F^{\prime }_{N}$
of
${\mathcal {F}}^{\prime }_N$
can be defined over
${\mathbb {Q}}$
, an assertion for which we provide a proof.
Rohrlich [Reference Rohrlich17] (see also Vélu [Reference Vélu18]) has determined the cuspidal subgroup of
$F_N$
. In particular, he has shown that any cuspidal divisor on
$F_N$
is of order dividing N. This description plays a key role in justifying the existence of the Heisenberg covering. We show that, by going further in the descending central series of
$\Gamma (2)$
,
$X^{\prime }_N$
is covered by a modular curve
$X^{\prime \prime }_N$
, in such a way that
$X^{\prime \prime }_N$
is still an abelian covering of the Fermat curve
$X_{N}$
. We do not describe algebraically
$X^{\prime \prime }_N$
.
We note that there has been a considerable interest in the cuspidal group of the Fermat curve. For instance, in [Reference Mazur10, p. 39], Mazur draws (or rather “stretches”) an analogy between Fermat curves and modular curves. Such an analogy is somewhat strengthened by the fact that the Heisenberg covering is analogous to the familiar Shimura covering
$X_1(N)\rightarrow X_0(N)$
between modular curves.
Like Murty and Ramakrishnan, our goal had been to illustrate our study of non-congruence subgroups by examining Heisenberg curves. We can not determine in general whether such curves satisfy the Manin–Drinfeld principle. But we can show easily that the principle holds for
$N=3$
. Furthermore, for
$N=3$
, we study the connection between
$F^{\prime }_{3}$
and various modular curves. By contrast, we have the following theorem for
$N=5$
:
Theorem 1.2 There exists a cuspidal divisor on
$X^{\prime }_5$
whose class in the Jacobian of
$X^{\prime }_5$
is of infinite order.
Let
$\bar \Gamma '(2)$
be the subgroup of index
$3$
of
$\bar \Gamma (2)$
obtained by pulling back the
$2$
-Sylow subgroup of
$\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Let
$\Gamma $
be a congruence subgroup of
$\bar \Gamma (2)$
. Consider the correspondence
$X^{\prime }_N\rightarrow X_\Gamma $
obtained by combining pulling back to the modular curve
$X_{\Gamma \cap \Phi ^{\prime }_N}$
with pushing to
$X_\Gamma $
. It produces a morphism of abelian varieties between the Jacobians or Riemann surfaces
$\theta _{N,\Gamma }$
:
$J^{\prime }_N\rightarrow J_\Gamma $
. In view of the following statement, we can hardly have any hope of establishing a limited form of the Manin–Drinfeld principle for Heisenberg curves using the classical Manin–Drinfeld theorem for congruence subgroups.
Theorem 1.3 The morphism
$\theta _{N,\Gamma }$
is zero if and only if either
$3 \nmid N$
or
$\Gamma $
is not contained in
$\bar \Gamma '(2)$
. If
$3 \mid N$
and
$\Gamma $
is contained in
$\bar \Gamma '(2)$
, the image of
$\theta _{N,\Gamma }$
is isogenous to an elliptic curve with j-invariant
$0$
. Furthermore, when
$\Gamma $
is contained in
$\bar \Gamma '(2)$
,
$\theta _{3,\Gamma }$
has finite kernel.
The proof of Theorem 1.3 is a translation of a group theoretic statement: any term of the lower central series of
$\bar \Gamma (2)$
is essentially dense in adelic completions of
$\bar \Gamma (2)$
(see Proposition 2.10). In addition to these results of algebraic nature, we give a combinatorial description of the homology of the Riemann surface
$X^{\prime }_{N}$
, by a method similar to Manin’s presentation, but following the variant introduced in [Reference Merel12]. This might have an interest of its own. But it does not help us for establishing our other results.
One of the referees noted connections to the work of Anderson and Ihara [Reference Anderson and Ihara1], as well as unpublished computations of Deligne. We hope that all this will be made explicit in the future.
2 Heisenberg groups and the lower central series of
$\bar \Gamma (2)$
2.1 The Heisenberg group
The Heisenberg group is the algebraic group of
$3\times 3$
unipotent upper triangular matrices. Set:
$x=\begin {pmatrix} 1 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
,
$y=\begin {pmatrix} 1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end {pmatrix}$
, and
$z=\begin {pmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end {pmatrix}$
.
Those elements satisfy the relations
$xz=zx$
,
$yz=zy$
, and
$z=xyx^{-1}y^{-1}=[x,y]$
. Thus, one obtains a presentation of the Heisenberg group over the integers. Note the formula, for a, b,
$c\in \mathbf {Z},$
$$\begin{align*}x^{a}z^{b}y^{c}=\begin{pmatrix} 1 & a & b\\ 0 & 1 & c\\ 0 & 0 & 1\\ \end{pmatrix}. \end{align*}$$
From that perspective, the group law is given by
$$ \begin{align*}x^{a}z^{b}y^{c}x^{a'}z^{b'}y^{c'}=x^{a+a'}z^{b+b'+a'c}y^{c+c'}. \end{align*} $$
The Heisenberg group
$H_{\mathbf {Z}}$
over
$\mathbf {Z}$
can be identified with
$\mathbf {Z}^{3}$
with the previous group law. The abelianization of
$H_{\mathbf {Z}}$
is freely generated by the images of x and y and is thus isomorphic to
$\mathbf {Z}^{2}$
. Thus,
$H_{\mathbf {Z}}$
is a central extension of
$\mathbf {Z}^{2}$
by
$\mathbf {Z}$
.
Let M and N be natural integers. Let L be a common divisor of M and N. Let
$H_{M,N,L}$
be the quotient group of
$H_{\mathbf {Z}}$
spanned by x and y with relations
$xz=zx$
,
$yz=zy$
,
$z=xyx^{-1}y^{-1}$
, and
$x^{N}=y^{M}=z^{L}=1$
. Such a group can be identified (as a set) with
$\mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/L\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
via the inverse of the map
$(a,b,c)\mapsto x^{a}z^{b}y^{c}$
.
Note the map
$H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
is coming from the abelianization.
Let
$M'$
,
$N'$
, and
$L'$
be integer
$\ge 1$
such that
$M|M'$
,
$N|N'$
, and
$L|L'$
. The canonical group homomorphism
$H_{M',N',L'}\rightarrow H_{M,N,L}$
is surjective. Its kernel is generated by
$\{x^{M},y^{N}\}$
. Since
$[x^{M},y^{N}]=z^{NM}$
, this kernel is abelian if and only if
$L'|NM$
.
Proposition 2.1 Let T be the lower common multiple of M and N. The group
$H_{M,N,L}$
is of exponent T if T is odd or
$T/L$
is even. It is of exponent
$2T$
otherwise. In particular
$H_{N,N,N}$
, for N odd, and
$H_{N,N,N/2}$
, for N even, are of exponent N.
Proof Let
$\alpha $
,
$\beta \in H_{M,N,L}$
in the subgroups generated by x and y, respectively. Let
$e=T$
if T is odd or
$T/L$
is even. Let
$e=2T$
otherwise. Since
$[\alpha ,\beta ]$
belongs to the center of
$H_{M,N,L}$
, it is of order dividing L. Moreover, one has
$(\alpha \beta )^{n}=\alpha ^{n}[\alpha ,\beta ]^{n(n-1)/2}\beta ^{n}$
, which vanishes if
$n=e$
. By this calculation, one has
$(xy)^{n}=x^{n}z^{n(n-1)/2}y^{n}$
, which shows that
$xy$
is of order T.
Since the group
${\bar \Gamma }(2)=\Gamma (2)/\{\pm 1\}$
is freely generated by A and B, one gets a surjective group homomorphism
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}$
which sends A and B to x and y, respectively. Its kernel is
$[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
. Every (necessarily nilpotent) finite quotient group of
${\bar \Gamma }(2)$
which factorizes through
${\bar \Gamma }(2)/[{\bar \Gamma }(2),[{\bar \Gamma }(2),{\bar \Gamma }(2)]]$
is isomorphic to one of the groups
$H_{M,N,L}$
.
Denote by
$\Gamma _{M, N, L}$
the kernel of the map:
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{M,N,L}$
.
2.2 The lower central series
Recall that the lower central series
$(G_k)_{k\ge 1}$
of a group G is defined recursively by
$G_1=G$
and
$G_{k+1}=[G_k,G]$
. The quotient
$G_k/G_{k+1}$
is then an abelian group. When G is a free group generated by the family
$(t_i)_{i\in I}$
,
$G_k/G_{k+1}$
is a free abelian group generated (not freely) by the classes of the commutators of weight k on the generators, i.e., by the
$[t_{i_1},\dots ,t_{i_k}]$
, where the indices run through any sequence
$\{1,2,\dots ,k\}\rightarrow I$
[Reference Hall6, Theorem 10.2.3]. When, furthermore, I is finite of cardinality m, the rank
$r_k$
of
$G_k/G_{k+1}$
is given by Witt’s formula, involving the necklace polynomial,
$$ \begin{align*}r_k(G)=\frac{1}{k}\sum_{d|k}\mu(d)m^{k/d}, \end{align*} $$
where
$\mu $
is the Möbius function. In particular, the lower central series
$({\bar \Gamma }(2)_k)_{k\ge 1}$
of
${\bar \Gamma }(2)$
satisfies
$r_1({\bar \Gamma }(2))=2$
,
$r_2({\bar \Gamma }(2))=1$
,
$r_3({\bar \Gamma }(2))=2$
, and
$r_4({\bar \Gamma }(2))=3$
. The corresponding generators of
${\bar \Gamma }(2)_k/{\bar \Gamma }(2)_{k+1}$
for
$k=1$
,
$2$
,
$3$
are the classes of
$\{A,B\}$
,
$\{C\}$
, and
$\{[C,A],[C,B]\}$
, respectively. Therefore, one has a surjective group morphism
$\phi _1$
:
${\bar \Gamma }(2)\rightarrow {\mathbb {Z}}^2$
such that
$\phi _1(A)=(1,0)$
and
$\phi _1(B)=(0,1)$
. Its kernel is
${\bar \Gamma }(2)_2$
. Moreover, one gets a group isomorphism:
${\bar \Gamma }(2)_1/{\bar \Gamma }(2)_{3}\simeq H_{\mathbf {Z}}$
.
Next, we have the surjective group morphism
$\phi _2$
:
${\bar \Gamma }(2)_2\rightarrow {\mathbb {Z}}$
, such that
$\phi _2(C)=1$
. Its kernel is
${\bar \Gamma }(2)_3$
. We can now describe
$\phi _3$
:
${\bar \Gamma }(2)_3\rightarrow {\mathbb {Z}}^2$
such that
$\phi _3([C,A])=(1,0)$
and
$\phi _3([C,B])=(0,1)$
. Something interesting happens at that stage.
For k integer
$\ge 2$
, the extension
$1\rightarrow G_{k}/G_{k+1}\rightarrow G_{k-1}/G_{k+1}\rightarrow G_{k-1}/G_k\rightarrow 1$
is central. Consequently, since
$r_2({\bar \Gamma }(2))=1$
, the group
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
is abelian, and free of rank
$3$
. Of course, the extension
$1\rightarrow {\bar \Gamma }(2)_{2}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_2\rightarrow 1$
is not central.
Proposition 2.2 There exists a group isomorphism
$\psi $
:
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4\simeq {\mathbb {Z}}^3$
given by
$C\mapsto (0,0,1)$
,
$[C,A]\mapsto (1,0,0)$
, and
$[C,B]\mapsto (0,1,0)$
. One has, for
$\gamma \in {\bar \Gamma }(2)$
and
$\delta \in \bar \Gamma (2)_2$
, the formula
$$ \begin{align*}\psi(\gamma\delta\gamma^{-1})=(-\phi_1(\gamma)\phi_2(\delta),0)+\psi(\delta), \end{align*} $$
or equivalently
$$ \begin{align*}\psi([\delta,\gamma])=(\phi_1(\gamma)\phi_2(\delta),0). \end{align*} $$
In particular, one has, for i,
$j\in {\mathbb {Z}}$
, the formula
$\psi (A^iB^jC^kB^{-j}A^{-i})=(-ki,-kj,k)$
.
Proof Given that
$\{[C,A],[C,B]\}$
is basis of the
${\mathbb {Z}}$
-module
${\bar \Gamma }(2)_3/{\bar \Gamma }(2)_4$
, and C is a basis of the
${\mathbb {Z}}$
module
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_3$
, any lifting of C modulo
${\bar \Gamma }(2)_3$
, to a class
$C'$
modulo
${\bar \Gamma }(2)_4$
gives a basis
$\{[C,A],[C,B], C'\}$
of
${\bar \Gamma }(2)_2/{\bar \Gamma }(2)_4$
. The choice
$C=C'$
is evidently suitable, but is somewhat arbitrary.
One has
$$ \begin{align*}\psi(\gamma\delta\gamma^{-1})=\psi(\gamma\delta C^{-\phi_2(\delta)}\gamma^{-1}C^{\phi_2(\delta)}\delta^{-1}\delta C^{-\phi_2(\delta)}\gamma C^{\phi_2(\delta)}\gamma^{-1}). \end{align*} $$
Since
$\delta C^{-\phi _2(\delta )}\in \bar \Gamma (2)_3$
, the factor
$\gamma \delta C^{-\phi _2(\delta )}\gamma ^{-1}C^{\phi _2(\delta )}\delta ^{-1}$
belongs to
$\bar \Gamma (2)_4$
; hence its image by
$\psi $
vanishes. So we get
$$ \begin{align} \psi(\gamma\delta\gamma^{-1})=\psi(\delta)-\phi_2(\delta)\psi(C)+\phi_2(\delta)\psi(\gamma C\gamma^{-1}), \end{align} $$
which translates into
$$ \begin{align*}\psi([\delta,\gamma])=\phi_2(\delta)\psi([C,\gamma]). \end{align*} $$
It remains to determine
$\psi ([C,\gamma ])$
. Let
$\gamma _1$
,
$\gamma _2\in {\bar \Gamma }(2)$
. One has
$$ \begin{align} (\gamma_1\gamma_2)\delta(\gamma_1\gamma_2)^{-1}=[\gamma_1,\gamma_2][\gamma_2,[\gamma_1,\delta]][\gamma_1,\delta][\gamma_2,\delta]\delta[\gamma_2,\gamma_1]. \end{align} $$
Since
$[\gamma _2,[\gamma _1,\delta ]]$
is a commutator of degree
$4$
, it is in the kernel of
$\psi $
. It follows that the map
$\gamma \mapsto \psi (\gamma \delta \gamma ^{-1})$
is a group homomorphism from
$\bar \Gamma (2)$
to
${\mathbb {Z}}^2$
. For
$\delta =C$
,
$\gamma =A$
(resp.
$\gamma =B$
), one has
$\psi (\gamma \delta \gamma ^{-1})=-(\psi _1(\gamma ),0)$
, hence the latter equality is true for all
$\gamma \in \bar \Gamma (2)$
. Thus, one gets
$$ \begin{align*}\psi([C,\gamma])=(\phi_1(\gamma),0), \end{align*} $$
which gives the main formula. It remains to apply this to
$\gamma =A^iB^j$
and
$\delta =C^k$
to obtain the final formula.
The exact sequence
$1\rightarrow {\bar \Gamma }(2)_{3}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_{4}\rightarrow {\bar \Gamma }(2)_{1}/{\bar \Gamma }(2)_3\rightarrow 1$
identifies to a central group extension
$$ \begin{align*}0\rightarrow {\mathbb{Z}}^2\rightarrow H^{\prime}_{\mathbb{Z}}\rightarrow H_{\mathbb{Z}}\rightarrow 1. \end{align*} $$
2.3 The groups
$\Phi _N$
,
$\Phi ^{\prime }_N$
, and
$\Phi ^{\prime \prime }_N$
We denote the group
$\Gamma _{N,N,1}$
by
$\Phi _N$
. It is the kernel of the group homomorphism
$\bar \phi _1$
:
${\bar \Gamma }(2)\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^2$
, which maps A to
$(1,0)$
and B to
$(0,1)$
(and thus C to
$(0,0)$
). A system of representatives for the cosets
$\Phi _N \backslash {\bar \Gamma }(2)$
is given by
$A^i B^j$
with
$i,j \in \{0,1\dots (N-1)\}$
. The structure of
$\Phi _N$
is probably well-known, but we could not find a complete reference for a presentation
$\Phi _N$
.
Proposition 2.3 The group
$\Phi _N$
is generated by
$U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
. Moreover,
$\Phi _N$
has presentation
$$\begin{align*}<A^N, B^N, T_{i,j}, 0\le i,j\le N-1 |[A^N,B^N]=\prod\limits_{i=0}^{N-1}\prod\limits_{j=0}^{N-1}T_{N-1-i,j}>. \end{align*}$$
Proof The group
$\Phi _N$
is generated by
$U=\{A^N,B^N, A^iB^jCB^{-j}A^{-i}/0\le i,j\le N-1\}$
(see [Reference Lang7, Reference Rohrlich17]). By the Nielsen–Schreier theorem,
$\Phi _N$
, being a free subgroup of index
$N^2$
of a free group on two generators, is free on
$N^2+1$
generators. A relation between the
$N^2+2$
exhibited generators in U presents itself:
$$ \begin{align} A^NB^NA^{-N}B^{-N}=\prod_{i=0}^{N-1}\prod_{j=0}^{N-1}A^{N-1-i}B^jCB^{-j}A^{i+1-N}. \end{align} $$
One of the exhibited generators in U can be expressed in terms of the
$N^2+1$
remaining elements of U. Thus, we get a presentation by generators and relations of
$\Phi _N$
.
Set
$N'=N$
if N is odd, and
$N'=N/2$
if N is even.
We set
$\Phi ^{\prime }_N=\Gamma _{N,N,N'}$
. It is the subgroup of
$\Phi _N$
obtained as the kernel of the morphism
$\bar \phi _2$
:
$\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
which vanishes on
$A^N$
and
$B^N$
and takes the value
$1$
on
$A^iB^jCB^{-j}A^{-i}$
for i, j integers.
Alternately,
$\Phi ^{\prime }_N$
is the kernel of the composed map
${\bar \Gamma }(2)\rightarrow H_{\mathbf {Z}}\rightarrow H_{N,N,N'}$
. Thus, the composed map
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
extends to a map
$\bar \phi _2$
:
$\Phi _N\rightarrow {\mathbb {Z}}/N'{\mathbb {Z}}$
, with kernel
$\Phi ^{\prime }_N$
. It vanishes on
$A^N$
and
$B^N$
.
Proposition 2.4 The composed map
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^3$
extends to a group homomorphism
$$ \begin{align*}\bar\psi: \Phi_N\rightarrow ({\mathbb{Z}}/N'{\mathbb{Z}})^3, \end{align*} $$
which vanishes on
$A^N$
and
$B^N$
and, for
$\gamma \in \bar \Gamma (2)$
and
$\delta \in \Phi _N$
, satisfies
$$ \begin{align} \bar\psi(\gamma\delta\gamma^{-1})=(-\bar\phi_1(\gamma)\bar\phi_2(\delta),0)+\bar\psi(\delta). \end{align} $$
In particular, for i, j,
$k\in {\mathbb {Z}}$
, one has
$$ \begin{align} \bar\psi(A^iB^jC^kB^{-j}A^{-i})=(-ik,-jk,k). \end{align} $$
Proof It follows from the presentation of
$\Phi _N$
that formula 2.5 defines a morphism
$\Phi _N\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
(it vanishes on the exhibited relation 2.3 between the generators). Such a morphism coincides with the composed map
$[{\bar \Gamma }(2),{\bar \Gamma }(2)]\rightarrow {\mathbb {Z}}^3\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^3$
, by the formula we established on
$\psi $
.
The formula 2.4 is valid whenever
$\delta \in \bar \Gamma (2)_2$
, by 2.1. Since
$\Phi _N$
is generated by
$\bar \Gamma (2)_2$
together with
$A^N$
and
$B^N$
, it remains to prove 2.4 for
$\delta =A^N$
and
$\delta =B^N$
. Consider the case
$\delta =B^N$
for instance (the other case is similar). Let us use the formula 2.2 again. We get, for
$\gamma _1$
,
$\gamma _2\in \bar \Gamma (2)$
, (leaving out opposite terms)
$$ \begin{align*}\bar\psi(\gamma_1\gamma_2 B^N\gamma_2^{-1}\gamma_1^{-1})=\bar\psi([\gamma_2,[\gamma_1,B^N]])+\bar\psi([\gamma_1,B^N])+\bar\psi([\gamma_2,B^N])+\bar\psi(B^N). \end{align*} $$
We have
$\bar \psi (B^N)=0$
, and
$\bar \psi ([\gamma _2,[\gamma _1,B^N]])$
is the reduction modulo N of
$\psi ([\gamma _2,[\gamma _1,B^N]])$
. One has
$\psi ([\gamma _2,[\gamma _1,B^N]])=-(\phi _1(\gamma _2)\phi _2([\gamma _1,B^N],0)$
. But
$\phi _2([\gamma _1,B^N])\in N{\mathbb {Z}}$
. So we have proved that the map
$\gamma \mapsto \bar \psi (\gamma B^N\gamma ^{-1})$
is a group homomorphism. It remains to prove that the formula 2.4 holds for
$\gamma =A$
and
$\gamma =B$
(still in the configuration where
$\delta =B^N$
). Only the case
$\gamma =A$
is of interest. We have
$$ \begin{align*}\bar\psi(AB^NA^{-1})=\bar\psi(AB^NA^{-1}B^{-N}). \end{align*} $$
As
$AB^NA^{-1}B^{-N}\in \bar \Gamma (2)_2$
,
$\bar \psi (AB^NA^{-1}B^{-N})$
is the reduction modulo N of
$\psi (AB^NA^{-1}B^{-N})$
. We use the identity
$$ \begin{align*}AB^NA^{-1}B^{-N}=(ABA^{-1})^NB^{-N}=(ABA^{-1}B^{-1}B)^NB^{-N}=CBCB^{-1}B^2CB^{-2}\dots B^{N-1}CB^{1-N}\kern-1pt. \end{align*} $$
The right-hand side is a product of generators of
$\Phi _N$
. We can apply 2.5
$$ \begin{align*}\psi(AB^NA^{-1}B^{-N})=\sum_{i=0}^{N-1}\psi(B^iCB^{-i})=\sum_{i=0}^{N-1}(0,-i,0)=(0,N(N-1)/2,0). \end{align*} $$
Since
$N'=\mathrm {gcd}(N,N(N-1)/2)$
, we have indeed that
$\bar \psi (AB^NA^{-1}B^{-N})=0$
.
Remark 2.5 Let
$N"=N'$
if N is prime to
$3$
, and
$N"=N'/3$
otherwise. The appearance of the denominator
$2$
(for
$N'$
) and now
$3$
(for
$N"$
) is related to Bernoulli numbers. We suspect that ultimately it is related to the mixed Tate motives that have been discovered by Deligne in his study of the nilpotent completion of the fundamental group of the projective line deprived of three points [Reference Deligne, Ihara, Ribet and Serre4].
We define
$\Phi ^{\prime \prime }_N$
as the kernel of the composed map
$\Phi _{N}\rightarrow ({\mathbb {Z}}/N'{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})\rightarrow ({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
Corollary 2.6 The exact sequence
$$ \begin{align*}0\rightarrow \Phi_N'/\Phi_N"\rightarrow {\bar\Gamma}(2)/\Phi_N"\rightarrow {\bar\Gamma}(2)/\Phi_N'\rightarrow 0 \end{align*} $$
makes of the group
${\bar \Gamma }(2)/\Phi _N"$
a central extension of the Heisenberg group
$H_{N,N,N'}$
by
$({\mathbb {Z}}/N"{\mathbb {Z}})^2$
.
Proof It follows from formula 2.4, as
$\bar \phi _2$
vanishes on
$\Phi ^{\prime }_N$
.
We denote by
$H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
the group
${\bar \Gamma }(2)/\Phi _N"$
.
Proposition 2.7 The group
$H^{\prime }_{{\mathbb {Z}}/N{\mathbb {Z}}}$
is of exponent N. In other words, for every
$\gamma \in \bar \Gamma (2)$
, one has
$\gamma ^N\in \Phi ^{\prime \prime }_N$
.
Proof It relies on relations for commutators, that, we presume, are well-known. Let G be a group. Suppose
$G_4$
is trivial. Then
$G_3$
is contained in the center of G. Let
$\alpha $
,
$\beta \in G$
. Set
$\gamma =[\alpha ,\beta ]$
,
$\alpha '=[\gamma ^{-1},\alpha ]$
, and
$\beta '=[\gamma ^{-1},\beta ]$
. Let
$n \in \mathbb {N} \cup \{0\}$
be an integer. One has the relation
$$ \begin{align} \beta^n\alpha=\alpha\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime}{-\frac{n(n-1)}{2}}. \end{align} $$
We prove it by induction on n. Indeed, it holds for
$n=0$
. Suppose it holds for some value of n. We have
$$ \begin{align*}\beta^{n+1}\alpha=\beta\alpha\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-n(n-1)/2}=\gamma^{-1}\alpha\beta\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-\frac{n(n-1)}{2}}. \end{align*} $$
We use the relations
$\gamma ^{-1}\beta =[\gamma ^{-1},\beta ]\beta \gamma ^{-1}=\beta ' \beta \gamma ^{-1}$
,
$\gamma ^{-1}\alpha =[\gamma ^{-1},\alpha ]\alpha \gamma ^{-1}=\alpha ' \alpha \gamma ^{-1}$
, and
$\beta \gamma ^{-n}=\beta ^{\prime -n} \gamma ^{-n}\beta $
. Using the fact that
$\alpha ', \beta ' \in Z(G)$
, we get
$$ \begin{align*} \beta^{n+1}\alpha &= \gamma^{-1}\alpha\beta\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha' \alpha \gamma^{-1} \beta \gamma^{-n} \alpha^{\prime n} \beta^{\prime-\frac{n(n-1)}{2}}\\ &= \alpha\gamma^{-n-1}\beta^{n+1}\alpha^{\prime n+1}\beta^{\prime-n-n(n-1)/2} \end{align*} $$
which is the desired formula. We pass to the next step. We now claim that
$$ \begin{align} (\alpha\beta)^n=\alpha^n\gamma^{-{n\choose 2}}\beta^n\alpha^{\prime{n+1 \choose 3}}\beta^{\prime-{n \choose 3}}. \end{align} $$
We proceed again by induction on n. This is true for
$n=1$
. We suppose the formula holds for a certain value of n. We get
$$ \begin{align*}(\alpha\beta)^{n+1}=(\alpha \beta)^n \cdot (\alpha\beta)=\alpha^n\gamma^{-{n \choose 2}}\beta^n \cdot (\alpha \beta)\alpha^{\prime{n+1 \choose 3}}\beta^{\prime-{n \choose 3}}. \end{align*} $$
Using the formula 2.6, we get
$$ \begin{align*}(\alpha\beta)^{n+1}=\alpha^n\gamma^{-{n \choose 2}}\alpha\gamma^{-n}\beta^n\alpha^{\prime n}\beta^{\prime-{n \choose 2}} \beta \alpha^{\prime{n+1 \choose 3}}\beta^{\prime-{n \choose 3}}. \end{align*} $$
We now use the formula
$\gamma ^{-{n\choose 2} }\alpha =\alpha ^{\prime {n\choose 2}}\alpha \gamma ^{-{n\choose 2}}$
and the centrality of
$\alpha '$
and
$\beta '$
to get
$$ \begin{align*}(\alpha\beta)^{n+1}= \alpha^n\gamma^{-{n\choose 2}-n}\beta^n\alpha^{\prime{n+1 \choose 3}+{n\choose 2}+n}\beta^{\prime-{n \choose 3}-{n\choose 2}}= \alpha^n\gamma^{-{n+1\choose 2}}\beta^n\alpha^{\prime{n+2\choose 3}}\beta^{\prime-{n +1\choose 3}} \end{align*} $$
which establishes 2.7.
The Nth powers of both A and B belong to
$\Phi ^{\prime \prime }_{N}$
(Proposition 2.4). The
$N'$
th, and therefore the
${N\choose 2}$
, power of any commutator belongs to
$\Phi ^{\prime \prime }_{N}$
, since
$\Phi ^{\prime }_{N}$
contains
$\bar \Gamma (2)_{2}$
. Similarly, the
$N"$
th power, and therefore the
${N\choose 3}$
and
${N+1\choose 3}$
powers, of an element of
$\bar \Gamma (2)_{3}$
belongs to
$\Phi ^{\prime \prime }_{N}$
. We can combine these remarks with the formula 2.7 for
$n=N$
, to establish that, if the Nth powers of
$\alpha $
and
$\beta $
both belong to
$\Phi ^{\prime \prime }_{N}$
, one has
$(\alpha \beta )^{N}\in \Phi ^{\prime \prime }_{N}$
. The proposition follows, since
$\{A,B\}$
generates
$\bar \Gamma (2)$
.
Remark 2.8 Let p be prime number. Stallings introduced the lower p-central series
$(S_{k})_{k\ge 1}$
as a particular case for
$N=p$
of the following construction. One has
${S_1=G}$
, and, for
$k\ge 2$
,
$S_{k+1}=[G,S_k](S_k)^N$
, where the latter expression is the subgroup of G generated by
$[G,S_k]$
and
$(S_k)^N$
. Note that, when
$G= {\bar \Gamma }(2)$
, one has
${S_2=[{\bar \Gamma }(2),{\bar \Gamma }(2)]{\bar \Gamma }(2)^N=\Phi _N}$
and
$S_3=[{\bar \Gamma }(2),\Phi _N]\Phi _N^N$
. Note that
$S_3\subset \Phi _N'\subset S_2$
. Since
$A^N$
and
$B^N$
do not belong to
$S_3$
, the groups
$S_3$
and
$\Phi ^{\prime }_N$
do not coincide.
2.4 Odd adelic completions
Recall that, for
$k\ge 1$
,
${\bar \Gamma }(2)_k$
is the kth term in the lower central series of
${\bar \Gamma }(2)$
. Let
$D_3=\{\pm \mathrm {Id}, \pm \begin {pmatrix} 0 & -1 \\ 1 & 0 \\ \end {pmatrix}, \pm \begin {pmatrix} -1 & 1 \\ 1 & 1 \\ \end {pmatrix}, \pm \begin {pmatrix} 1 & 1 \\ 1 & -1 \\ \end {pmatrix}\}$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
be the index
$3$
,
$2$
-Sylow subgroup of
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. It is isomorphic to the Klein group.
Recall that the derived subgroup of
$\mathrm {PSL}_{2}({\mathbb {Z}})$
is the projective congruence subgroup of level
$6$
whose image in
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is
$D_{3}$
, and whose image in
$\mathrm { PSL}_{2}({\mathbb {Z}}/2{\mathbb {Z}})$
is cyclic of order
$3$
.
Let
$$\begin{align*}\hat{\mathbb{Z}}_{\mathrm{odd}}=\varprojlim_{n\,\mathrm{odd}} {\mathbb{Z}}/n{\mathbb{Z}}\simeq\prod_{p\ne2}{\mathbb{Z}}_{p} \end{align*}$$
be the profinite completion of
${\mathbb {Z}}$
away from the prime
$2$
. Let
$\hat D_{\mathrm {odd}}$
be the inverse image of
$D_{3}$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
Proposition 2.9 The image of
${\bar \Gamma }(2)_2$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
is equal to
$D_{3}$
. For p prime,
$p>3$
, its image modulo p is
$\mathrm {PSL}_{2}({\mathbb {Z}}/p{\mathbb {Z}})$
.
Proof Indeed, the images of
${\bar \Gamma }(2)$
and
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
coincide by weak approximation. Thus,
${\bar \Gamma }(2)_2$
modulo
$3$
coincides with the derived subgroup of
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
, which in turn is the reduction modulo
$3$
of the derived subgroup of
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
. The second assertion is proved similarly.
Proposition 2.10 Let k be an integer
$\ge 2$
. The closure of
${\bar \Gamma }(2)_k$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to
$\hat D_{\mathrm {odd}}$
.
Proof We prove this first for
$k=2$
. Let n be an odd integer divisible by
$3$
. Let
$D_n$
be the inverse image of
$D_{3}$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. The image of
${\bar \Gamma }(2)_2$
modulo n coincide with the image of the derived subgroup of
$\mathrm {PSL}_{2}({\mathbb {Z}}))$
modulo n, which is a subgroup of index
$3$
of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Such a subgroup can only be
$D_n$
. Thus, we obtain the proposition for
$k=2$
.
We prove the proposition for
$k=3$
. Let
$I_n$
be the image of
${\bar \Gamma }(2)_3$
in
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Note that we have an exact sequence
$$\begin{align*}1\rightarrow K_n \rightarrow I_n\rightarrow D_3\rightarrow 1. \end{align*}$$
Since we have an exact sequence
$$\begin{align*}1\rightarrow \pm1+3\mathrm{M}_2( {\mathbb{Z}}/\frac{n}{3}{\mathbb{Z}})_0 \rightarrow \mathrm{PSL}_{2}({\mathbb{Z}}/n{\mathbb{Z}})\rightarrow \mathrm{PSL}_{2}({\mathbb{Z}}/3{\mathbb{Z}})\rightarrow 1, \end{align*}$$
where
$\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0$
is the subgroup of
$\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})$
made of matrices of trace
$0$
, the equality
$I_n=D_n$
would follow from the inclusion
$1+3\mathrm {M}_2( {\mathbb {Z}}/\frac {n}{3}{\mathbb {Z}})_0\subset K_n$
. It remains to establish the latter inclusion. Since
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
is equal to its derived subgroup when n is prime to
$6$
, by the Chinese remainder theorem, it is enough to prove it when n is a power of
$3$
.
It follows from the equality
$[(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0},\mathrm {SL}_2({\mathbb {Z}}_p)]=(1+p\mathrm {M}_2({\mathbb {Z}}_p))_{0}$
, valid for any prime p, and the fact that the closure of
${\bar \Gamma }(2)_2$
in
$\mathrm {PSL}_2({\mathbb {Z}}_3)$
contains
$[(1+3\mathrm {M}_2({\mathbb {Z}}_3))_{0}$
.
The general case
$k\ge 3$
of the proposition is now immediate. Indeed, since
${\bar \Gamma }(2)_3$
and
${\bar \Gamma }(2)_2$
have the same image modulo n, those images are the second and third, respectively, derived subgroups of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
. Thus, the lower central series of
$\mathrm {PSL}_{2}({\mathbb {Z}}/n{\mathbb {Z}})$
stabilizes to the image modulo n of
${\bar \Gamma }(2)_k$
for any
$k\ge 3$
.
Proposition 2.11 The closure of
$\Phi _{N}$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
$3$
does not divide N. It is
$\hat D_{\mathrm {odd}}$
if
$3$
divides N.
Proof If
$3$
does not divide N,
$\Phi _N$
contains a nonzero upper triangular matrix (for instance,
$A^{\prime N}$
) which is not the identity modulo
$3$
. Its closure in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains a maximal proper subgroup of index
$3$
, namely
$\hat D_{\mathrm {odd}}$
, and an element which is not in that subgroup. Therefore, the closure is
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
. If
$3$
divides N, since both
$A^{3N}$
and
$B^{3N}$
vanish modulo
$3$
, the images of
$\Phi _N$
and
${\bar \Gamma }(2)_2$
coincide in
$\mathrm {PSL}_{2}({\mathbb {Z}}/3{\mathbb {Z}})$
. Hence the result.
Proposition 2.12 The closure of
$\Phi ^{\prime }_{N}$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
if
$3$
does not divide N. It is
$\hat D_{\mathrm {odd}}$
if
$3$
divides N.
Proof The closure of
${\bar \Gamma }(2)_2$
and
${\bar \Gamma }(2)_3$
coincide modulo n for every n divisible by
$3$
, as we have just established. Thus, the closure of
$\Phi ^{\prime }_N$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
contains
${\bar \Gamma }(2)_2$
. Since the group
$\Phi ^{\prime }_{N}$
contains the matrices
$A^N$
and
$B^N$
, its closure contains
$\Phi _N$
. Thus, the closure of
$\Phi ^{\prime }_N$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
is equal to the closure of
$\Phi _{N}$
in
$\mathrm {PSL}_{2}(\hat {\mathbb {Z}}_{\mathrm {odd}})$
.
Let
$\bar \Gamma '(2)=\bar \Gamma (2)\cap \hat D_{\mathrm {odd}}$
. It is a subgroup of index
$3$
of
$\bar \Gamma (2)$
.
Corollary 2.13 Let
$\Gamma $
be a congruence subgroup of
$\bar \Gamma (2)$
. One has
$\Gamma \Phi ^{\prime }_N= \bar \Gamma '(2)$
if
$\Gamma \subset \bar \Gamma '(2)$
and
$3$
divides N. One has
$\Gamma \Phi ^{\prime }_N= \bar \Gamma (2)$
otherwise.
Let n be an even integer. In particular, one has
$\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma (2)$
if
$3$
does not divide either n or N. One has
$\Gamma (n)\Phi ^{\prime }_{N}=\bar \Gamma '(2)$
if
$3$
divides both n and N.
3 The associated Riemann surfaces
3.1 The Riemann surface
$X_{M, N,L}$
Denote by
$X_{M, N,L}$
the compactified modular curve defined by
$\Gamma _{M, N, L}$
.
Proposition 3.1 The genus
$g_{M, N,L}$
of the curve
$X_{M, N,L}$
is given by the following formulas. Denote by T the lowest common multiple of M and N. Suppose T is even and
$T/L$
is odd, then one has
$$\begin{align*}g_{M, N,L}:=g(X_{M, N,L})=(NML-NL-ML-NML/2T)/2+1. \end{align*}$$
Suppose T is odd or
$T/L$
is even, then one has
$$\begin{align*}g_{M, N,L}:=g(X_{M, N,L})=(NML-NL-ML-NML/T)/2+1. \end{align*}$$
Proof We use Riemann–Hurwitz formula for the morphism
$X_{N,M,L}\rightarrow X(2)$
. Since
$\Gamma (2)$
has no elliptic elements, the ramification points of this morphism reside entirely among the cusps.
Concerning the cusps above
$0$
(resp.
$\infty $
), note that the stabilizer of the rational number
$0$
(resp.
$\infty $
) in
$P\Gamma (2)$
is generated by B (resp. A). As the morphism
$X_{N,M,L}\rightarrow X(2)$
is Galois, the ramification index is independent of the chosen cusp, and is the order of the orbit of B (resp. of A) acting on
$\Gamma _{M,N,L}\backslash \Gamma (2)$
. This is N (resp. M) by definition of
$\Gamma _{M,N,L}$
. Concerning the cusps above
$1$
, the stabilizer in
$P\Gamma (2)$
of the rational number
$-1$
is generated by
$A^{-1}B$
. It remains to determine the order of
$A^{-1}B$
in
$\Gamma _{M,N,L}\backslash \Gamma (2)=H_{M,N,L}$
.
The abelianization provides a map:
$H_{M,N,L}\rightarrow \mathbf {Z}/M\mathbf {Z}\times \mathbf {Z}/N\mathbf {Z}$
which sends
$A^{-1}B$
to
$(1,-1)$
. The latter element is of order T, which leads us to examine the order of
$(A^{-1}B)^{T}$
in
$H_{M,N,L}$
. Denote by
$D=[A^{-1},B]$
. It belongs to and generates the center of
$H_{M,N,L}$
. It is of order L. Note the formula
$A^{-1}B=DBA^{-1}$
. Thus, one has
$(A^{-1}B)^{T}=D^{k}A^{-T}B^{T}$
in
$H_{M,N,L}$
, where k is the number of factors
$A^{-1}$
to the right of a factor B in the
$(A^{-1}B)^{T}$
written as a product of
$2T$
factors. One has
$k=1+2+\dots +(T-1)=T(T-1)/2$
. This is why the order of
$(A^{-1}B)^{T}$
is
$1$
if L is odd or if
$T/L$
is even. This order is
$2$
otherwise.
Thus, the ramification index e of any cusp above
$1$
is equal to T if L is odd or if
$T/L$
is even. It is
$2T$
otherwise. We can now apply the Riemann–Hurwitz formula for the dominant morphism
$X_{M,N,L}\rightarrow X(2)$
:
$$\begin{align*}2 g_{M, N,L}-2=-2d+\sum_{x \in X_{M, N, L}}(e_x-1). \end{align*}$$
We have
$d=|H_{M,N,L}|=MNL$
. One gets
$$\begin{align*}2 g_{M, N,L}-2=-2MNL+NL(M-1)+ML(N-1)+NML(1-1/e) \end{align*}$$
and
$$\begin{align*}g_{M, N,L}=NML-NL-ML-NML/e+1. \end{align*}$$
The lemma follows from the calculation of e.
3.2 The Riemann surfaces
$X_N$
,
$X^{\prime }_N$
, and
$X^{\prime \prime }_N$
All three groups
$\Phi _N$
,
$\Phi _N'$
, and
$\Phi _N"$
act on the upper half-plane
$\mathbb {H}$
. We denote, respectively, by
$X_N$
,
$X^{\prime }_N$
, and
$X^{\prime \prime }_N$
the corresponding completed modular curves.
Proposition 3.2 Both morphisms
$X^{\prime }_N\rightarrow X_N$
and
$X^{\prime \prime }_N\rightarrow X^{\prime }_N$
(and therefore
$X^{\prime \prime }_N\rightarrow X_N$
as well) are unramified. The covering
$X^{\prime }_{N}\rightarrow X_{N}$
is cyclic of degree
$N'$
. The covering
${X^{\prime \prime }_{N}\rightarrow X^{\prime }_{N}}$
is Galois with group
$({\mathbb {Z}}/N"{\mathbb {Z}})^{2}$
. The covering
$X^{\prime \prime }_{N}\rightarrow X_{N}$
is abelian with Galois group
$({\mathbb {Z}}/N"{\mathbb {Z}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
.
Proof The first statement needs only to be established for the morphism
$X^{\prime \prime }_N\rightarrow X_N$
. The ramification points can only reside at the cusps. To show that those cusps are unramified, we need only to show that their width in
$X^{\prime \prime }_N$
is equal to their width, equal to N, in
$X_N$
. Since the covering
$X^{\prime \prime }_N\rightarrow X_1$
is Galois, the width of a cusp of
$X_N"$
depends only on its image in the set of cusps
$\{0,1,\infty \}$
of
$X_1$
. We just need to look at the order of A, B and
$A^{-1}B$
in
${\bar \Gamma }(2)/\Phi ^{\prime \prime }_N$
. All three are of order N in the latter quotient.
The other assertions follow immediately from the properties of the groups
$\Phi _N$
,
$\Phi _N'$
, and
$\Phi _N"$
.
The Riemann surface
$X_N$
is isomorphic to the Riemann surface obtained from the complex points of the Fermat curve. The covering
$X_N'\rightarrow X_N$
is obtained from what we call Heisenberg covering of the Fermat curve by passing to the complex numbers.
We obtain the genus
$g_N$
and
$g_N'$
of the curves
$X_N$
and
$X_N'$
by our formulas for the genus of
$X_{N,M,L}$
. One has
$g_N=g_{N,N,1}=(N-1)(N-2)/2$
. Furthermore, if N is odd, one has
$g^{\prime }_{N}=g_{N,N,N}=(N^{3}-3N^{2}+2)/2=(N-1)(N^2-2N-2)/2$
. If N is even, one gets
$g^{\prime }_{N}=g_{N,N,N'}=(2N^3-5N^2+4)/4=(N-2)(2N^2-N-2)/4$
.
The genus of
$g_N"$
of the curve
$X_N"$
can be deduced from the Riemann–Hurwitz formula. Since we have a covering
$X^{\prime \prime }_N\rightarrow X^{\prime }_N$
of degree
$N^{\prime \prime 2}$
, one has
$$ \begin{align*}g^{\prime\prime}_N=N^{\prime\prime2}g^{\prime}_N-N^2+1. \end{align*} $$
The curve
$X^{\prime }_{N}$
possesses
$NN'$
cusps above each of the cusps
$0$
,
$1$
, and
$\infty $
of
$X(2)$
.
3.3 Some cases of small genus
Proposition 3.3 The genus g of the curve
$X_{M, N,L}$
is equal to
$0$
for the following values of
$(N,M,L)$
, and only for those values:
$(N,1,1)$
,
$(1,M,1)$
,
$(2,2,1)$
,
$(2,2,2)$
.
Proof The formula just established gives:
$2-2g=-L(MN-N-M-MN/e)$
. Thus,
$g=0$
implies that
$L=1$
or
$2$
.
If
$g=0$
and
$L=1$
, then one has
$MN-N-M-MN/e=-2$
and
$e=\mathrm {lcm}(M,N)$
. Thus,
$\mathrm {gcd}(M,N)$
divides
$2$
. If
$\mathrm {gcd}(M,N)=1$
, then one has
$MN-N-M-1=-2$
, and thus
$(M-1)(N-1)=0$
that is
$M=1$
or
$N=1$
. If
$\mathrm {gcd}(M,N)=2$
, one has
$MN-N-M-2=-2$
and thus
$(M-1)(N-1)=1$
; therefore one has
$(M,N)=(2,2)$
.
If
$g=0$
and
$L=2$
, then one has
$MN-N-M-MN/e=-1$
. If
$4$
divides neither M nor N, one has
$e=2\mathrm {lcm}(M,N)$
. Then
$\mathrm {gcd}(M,N)$
divides
$2$
, and is equal to
$2$
. Then one has
$MN-N-M-1=-2$
, as above. As
$L=2$
, the cases
$M=1$
and
$N=1$
are excluded; thus, one has
$(M,N)=(2,2)$
.
Proposition 3.4 The genus g of the curve
$X_{M, N,L}$
is equal to
$1$
for the following values of
$(N,M,L)$
, and only for those values (up to permutation of N and M):
$(3,2,1)$
,
$(4,2,1)$
,
$(4,2,2)$
,
$(3,3,1)$
,
$(3,3,3)$
.
The Jacobian varieties of those curves are elliptic curves endowed with automorphisms of order
$3$
,
$4$
,
$4$
,
$3$
, and
$3$
, respectively. Consequently, the j-invariants of those curves are
$0$
,
$1728$
,
$1728$
,
$0,$
and
$0$
, respectively.
Proof Consider again the formula:
$2-2g=-L(MN-N-M-MN/e)$
. Thus,
${g=1}$
amounts to
$MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=0$
. One has
$MN{\kern-1pt}-{\kern-1pt}N{\kern-1pt}-{\kern-1pt}M{\kern-1pt}-{\kern-1pt}MN/e=(N-2) (M-1)-2+M(1-N/e)$
. We can suppose that
$N>1$
and
$M>1$
(otherwise
$g=0$
).
If
$N=2$
, one gets
$M(1-2/e)=2$
. If
$L=1$
, then
$e=\mathrm {lcm}(M,2)$
. Thus,
$M-1=2$
or
$M-2=2$
. One has
$(N,M,L)=(2,3,1)$
or
$(N,M,L)=(2,4,1)$
.
If
$N=2$
and
$L=2$
, then
$e=2M$
or
$e=M$
. If
$e=M$
, then
$M-2=2$
. If
$e=2M$
, then
$M-1=2$
(absurd since
$L|M$
). One has
$(N,M,L)=(2,4,2)$
or
$(N,M,L)=(2,4,1)$
.
If
$N=3$
, then one has
$M-3+M(1-3/e)=0$
and
$e=\mathrm {lcm}(M,3)$
. One can suppose that
$M>2$
. Thus, one has
$M=3$
and
$L=1$
or
$L=3$
. One has
$(N,M,L)=(3,3,1)$
or
$(N,M,L)=(3,3,3)$
.
The case where
$M=2$
or
$M=3$
are treated similarly. If
$N>3$
and
$M>3$
, one has
$(N-2)(M-1)-2+M(1-N/e)>0$
, which precludes
$g=1$
.
The automorphisms come from the action of the image of A in
$H_{N,M,L}$
which stabilizes a cusp and therefore is an automorphism of an elliptic curve.
We can derive some information on the Manin–Drinfeld principle in the genus
$1$
cases.
Proposition 3.5 Divisors of the form
$(CP)-(P)$
, where P is any point (in particular, a cusp) of
$X_{3,3,3}$
(resp.
$X_{4,2,2}$
) and C acts via the map
$\bar \Gamma (2)\rightarrow H_{N,M,L}$
, are of order dividing
$3$
(resp.
$2$
).
Proof The canonical morphism
$X_{3,3,3}\rightarrow X_{3,3,1}$
is of degree
$3$
. It gives rise to an isogeny of degree
$3$
on the Jacobians by Albanese functionality. Thus, the kernel of this isogeny is of order
$3$
. Moreover, any divisor of the form
$(CP)-(P)$
is in the kernel of the isogeny.
3.4 The curve
$X'(2)$
Recall that the group
$\bar \Gamma '(2)$
is the subgroup of index
$3$
of
$\bar \Gamma (2)$
that is the inverse image of the
$2$
-Sylow subgroup of
$\mathrm {PSL}_2({\mathbb {Z}}/3{\mathbb {Z}})$
. Denote by
$X'(2)=X_{\Gamma '(2)}$
the corresponding modular curve.
Proposition 3.6 The curve
$X'(2)$
is of genus
$1$
and its j-invariant is
$0$
.
Proof Consider the morphism of degree
$d=3$
:
$X'(2)\rightarrow X(2)$
. Since none of the matrices A (generator of the stabilizer of the cusp
$\infty $
), B (generator of the stabilizer of the cusp
$0$
), and
$AB^{-1}$
(generator of the stabilizer of the cusp
$1$
) are not in
$\bar \Gamma (2)$
, the morphism is totally ramified at each of the three cusps of
$X(2)$
, and ramified only over those points. The Riemann–Hurwitz formula expresses the genus g of
$X'(2)$
as
$(2g-2)=-2d+\sum _P(e_P-1)=6-6=0$
(where P runs through points of ramification and
$e_P$
designates the ramification index at that point), hence
$g=1$
.
The curve
$X'(2)$
has an automorphism (the class of A in
$\bar \Gamma (2)/\bar \Gamma '(2)$
) of order
$3$
which leaves fixed the cusp
$\infty $
. Since it is of genus
$1$
, it is an elliptic curve of with an automorphism of order
$3$
. It has necessarily j-invariant
$0$
.
Remark 3.7 Since
$\Gamma _{3,3,3}=\Phi ^{\prime }_3$
is a subgroup of index
$3$
of
$\Gamma '(2)$
. One has a morphism
$X_{3,3,3}\rightarrow X'(2)$
of degree
$3$
. Both curves involved are of genus
$1$
, so we have an isogeny of degree
$3$
. Note that
$\bar \Gamma '(2)$
is a congruence subgroup of level
$12$
and a subgroup of index
$3$
of the derived subgroup
$\tilde \Gamma $
of
$\mathrm {PSL}_2({\mathbb {Z}})$
. The latter subgroup defined a modular curve
$X_{\tilde \Gamma }$
of genus
$1$
, which happens to have j-invariant
$0$
. Thus, we get an isogeny
$X'(2)\rightarrow X_{\tilde \Gamma }$
of degree
$3$
.
We now prove Theorem 1.3.
Proof The correspondence is obtained by composing pushing to
$X_{\Gamma. \Phi ^{\prime }_d}$
and pulling back to
$X_\Gamma $
. By Proposition 2.12, one has
$\Gamma. \Phi ^{\prime }_d=\bar \Gamma (2)$
except if
$3$
divides N and
$\Gamma $
is contained in
$\bar \Gamma '(2)$
. In the latter case,
$\theta _{N,\Gamma }$
factorizes through the Jacobian of
$X(2)$
, which is
$0$
. Otherwise, namely if
$3$
divides N and
$\Gamma $
is contained in
$\bar \Gamma '(2)$
,
$\theta _{N,\Gamma }$
factorizes through the surjective map
$J^{\prime }_N\rightarrow J'(2)$
. Since
$J'(2)$
is the Jacobian of a curve of genus
$1$
, and j-invariant
$0$
, it is an elliptic curve of j-invariant
$0$
. Moreover, the map
$J'(2)\rightarrow J_\Gamma $
has finite kernel. The result follows.
It is well-known that the modular curve
$X_0(27)$
has j-invariant
$0$
, and that the Fermat curve is a model for
$X_0(27)$
. We might expect a connection between
$X_0(27)$
and
$X^{\prime }_3$
. Let
$\Gamma =\bar \Gamma (2)\cap \Gamma _0(27)$
. It is a congruence subgroup. But it is not contained in
$\Gamma '(2)$
. Thus, if we apply Theorem 1.3 to the group
$\Gamma $
, we obtain, counterintuitively, the
$0$
-morphism
$J^{\prime }_3\rightarrow J_{\Gamma }$
. A fortiori, if we push forward
$J_\Gamma \rightarrow J_0(27)$
we obtain
$0$
.
3.5 Mixed homology groups
In [Reference Ejder5], the homology group of
$X_N$
relative to the whole set of cusps is thoroughly studied, by the method of Manin [Reference Manin9]. We found fruitful in [Reference Banerjee and Merel2] to consider the following slightly different point of view: for
$\Gamma $
a subgroup of finite index of
$\bar \Gamma (2)$
, the corresponding modular curve
$X_\Gamma $
covers
$X(2)$
, which admits three cusps:
$\Gamma (2)0$
,
$\Gamma (2)1$
, and
$\Gamma (2)\infty $
. Let
$\partial _\Gamma ^+$
(resp.
$\partial _\Gamma ^-$
) be the set of cusps above
$\Gamma (2)0\cup \Gamma (2)\infty $
(resp.
$\Gamma (2)1$
)). It is thus possible to consider the mixed homology group
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
(and its dual
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{+}, \partial _{\Gamma }^{-}; {{\mathbb {Z}}})$
). One gets a group isomorphism
$$\begin{align*}\xi_{\Gamma}^{+}: {\mathbb{Z}}[\Gamma\backslash\bar\Gamma(2)]\rightarrow \mathrm H_1(X_{\Gamma}-\partial_{\Gamma}^{-}, \partial_{\Gamma}^{+}; {{\mathbb{Z}}}) \end{align*}$$
which, for
$g\in \bar \Gamma (2)$
, associates to
$\Gamma g$
the class
$\xi _\Gamma (g)$
in
$\mathrm H_1(X_{\Gamma }-\partial _{\Gamma }^{-}, \partial _{\Gamma }^{+}; {{\mathbb {Z}}})$
of a path from
$g0$
to
$g\infty $
in the upper half-plane.
Consider now the case where
$\Gamma =\Phi ^{\prime }_N$
. To simplify notations, set
$\partial ^{+}=\partial ^+$
and
$\partial ^{-}=\partial ^-$
. Recall that we have a group isomorphism
$\Phi _N'\backslash \Gamma (2)\rightarrow H_{N,N,N'}$
which, for
$(a,b,c)\in ({{\mathbb {Z}}})^{3}$
, to
$\Phi ^{\prime }_NA^aC^cB^b$
associates
$x^az^cy^b$
. We get thus a group isomorphism
$$\begin{align*}{\mathbb{Z}}[ H_{N,N,N'}]\simeq \mathrm H_1(X^{\prime}_N-\partial^-,\partial^+;{\mathbb{Z}}). \end{align*}$$
For
$(a,b,c)\in ({{\mathbb {Z}}}/N{{\mathbb {Z}}})^{2}\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, set
$i(a,b,c)=\xi ^{+}_{\Phi ^{\prime }_N}(\Phi ^{\prime }_{N}A^{a}C^{c}B^{b})$
.
Thus,
$H_{N,N,N'}$
acts on the curve
$X^{\prime }_{N}$
, and transitively on the sets of cusps of
$X^{\prime }_{N}$
above
$0$
,
$1$
, and
$\infty $
, respectively. Thus, the stabilizer of a cusp is cyclic of order N.
The long exact sequence of relative homology yields:
$$\begin{align*}0 \rightarrow \mathrm H_1(X^{\prime}_N-\partial^-; {\mathbb{Z}}) \rightarrow \mathrm H_1(X^{\prime}_N-\partial^-,\partial^+;{\mathbb{Z}}) \xrightarrow{\delta_N} {\mathbb{Z}}[\partial^+]^0 \rightarrow 0, \end{align*}$$
where
$\delta _N$
is the boundary map. Similarly we have a dual exact sequence:
$$\begin{align*}0 \rightarrow {\mathbb{Z}}[\partial^-]^0\xrightarrow{\delta_N^*}\mathrm H_1(X^{\prime}_N-\partial^-,\partial^+;{\mathbb{Z}}) \rightarrow \mathrm H_1(X^{\prime}_N,\partial^+;{\mathbb{Z}}) \rightarrow 0, \end{align*}$$
where
$\delta _N^*$
is the dual boundary map. It induces
$$\begin{align*}0 \rightarrow {\mathbb{Z}}[\partial^-]^0\xrightarrow{\delta_N^*}\mathrm H_1(X^{\prime}_N-\partial^-;{\mathbb{Z}}) \rightarrow \mathrm H_1(X^{\prime}_N;{\mathbb{Z}}) \rightarrow 0. \end{align*}$$
Hence,
$\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
can be described as a subquotient of the group
$\mathrm H_1(X^{\prime }_N-\partial ^-,\partial ^+;{\mathbb {Z}})$
. We will make this explicit by spelling out the maps
$\delta _N$
and
$\delta _N^*$
.
The sets of cusps of
$X^{\prime }_N$
lying above
$\infty $
,
$0$
and
$1$
are, respectively,
$\Phi _N'\backslash \Gamma (2)/A^{{\mathbb {Z}}}$
,
$\Phi _N' \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
and
$\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}} $
. All three sets can be understood as follows.
Proposition 3.8 We have three bijective maps as follows:
$$\begin{align*}\Phi_N'\backslash \Gamma(2)/A^{{\mathbb{Z}}} \rightarrow ({\mathbb{Z}}/N{\mathbb{Z}})\times ({\mathbb{Z}}/N'{\mathbb{Z}}) \end{align*}$$
given by
$x^{a} z^cy^{b}\mapsto (b,c+ab)$
,
$$\begin{align*}\Phi_N' \backslash \Gamma(2)/B^{{\mathbb{Z}}} \rightarrow ({\mathbb{Z}}/N{\mathbb{Z}})\times ({\mathbb{Z}}/N'{\mathbb{Z}}) \end{align*}$$
given by
$x^a z^c y^{b}\mapsto (a,c)$
, and
$$\begin{align*}\Phi_N' \backslash \Gamma(2)/(AB^{-1})^{{\mathbb{Z}}} \rightarrow ({\mathbb{Z}}/N{\mathbb{Z}})\times ({\mathbb{Z}}/N'{\mathbb{Z}}) \end{align*}$$
given by
$x^a z^c y^{b}\mapsto (a+b,c-b(b+1)/2)$
.
Proof The first two identifications are straightforward. We establish the third one. Let k be an integer. One finds by induction on k,
$x^a z^c y^{b}(xy^{-1})^{k}=x^{a+k}z^{c-kb+k(k-1)/2}y^{b-k}$
. Since
$(a+k)+(b-k)=a+b$
and
$$\begin{align*}c-kb+k(k-1)/2-(b-k)(b-k+1)/2=c-b(b+1)/2, \end{align*}$$
the map passes indeed to the quotient
$\Phi _N' \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
. It is surjective (take
$b=0$
). Since there are
$NN'$
cusps above
$1$
, it is bijective.
Denote by
$j_\infty (b,c)$
the cusp
$\Phi _N'A^{a}C^{c-ab}B^bA^{N{\mathbb {Z}}}$
, for any
$a\in {\mathbb {Z}}$
, by
$j_0(a,c)$
the cusp
$\Phi _N'A^{a}C^{c}B^{b}B^{N{\mathbb {Z}}}$
, for any
$b\in {\mathbb {Z}}$
, and
$j_{1}(d,c)$
the cusp
$\Phi _N'A^{a}C^{c-b(b+1)/2}B^{b}(AB^{-1})^{N{\mathbb {Z}}}$
, for any a,
$b\in {\mathbb {Z}}$
such that
$a+b=d$
. With these conventions we can express
$\delta _{N}$
.
Proposition 3.9 Let a, b,
$c\in {\mathbb {Z}}$
. One has
$\delta _N(i(a,b,c))=j_\infty (b,c-ab)-j_0(a,c)$
.
Proof The boundary of the modular symbol
$\{A^{a}C^{c}B^{b}0, A^{a}C^{c}B^{b}\infty \}$
is
$$\begin{align*}[\Phi^{\prime}_{N}A^{a}C^{c}B^{b}A^{{\mathbb{Z}}}]-[\Phi^{\prime}_{N}A^{a}C^{c}B^{b}B^{{\mathbb{Z}}}], \end{align*}$$
which translates immediately into the claimed formula.
We use [Reference Banerjee and Merel2, Proposition 5] to determine
$\delta _N^*$
.
Proposition 3.10 One has, for
$d\in {\mathbb {Z}}/N{\mathbb {Z}}$
and
$c\in {\mathbb {Z}}/N'{\mathbb {Z}}$
,
$$\begin{align*}\delta_N^*(j_{1}(d,c))=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}i(a,b+1,c-b(b+1)/2)-i(a,b,c-b(b+1)/2). \end{align*}$$
Proof We just need to translate the third statement [Reference Banerjee and Merel2, Proposition 5]. With the notations of that proposition, we have
$w_{1}=N$
. It remains to use the third bijection of Proposition 3.8 and the definition of i.
Let
$S_{N}$
be the subgroup of
${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
formed by the elements of the form
$\sum \limits _{a,b,c}\lambda _{a,b,c}[a,b,c]$
, satisfying, for every
$(a,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
$\sum \limits _{b\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c}=0$
and, for every
$(b,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
, the relation
$\sum \limits _{a\in {\mathbb {Z}}/N{\mathbb {Z}}}\lambda _{a,b,c+ab}=0$
. By Proposition 3.9, its image by i has boundary
$0$
.
Let
$R_{N}$
be the subgroup of
${\mathbb {Z}}[({\mathbb {Z}}/N{\mathbb {Z}})^{2}\times {\mathbb {Z}}/N'{\mathbb {Z}}]$
spanned by elements of the form
$$\begin{align*}e_{c,d}=\sum_{\substack{a,b\in{\mathbb{Z}}/N{\mathbb{Z}},\\ a+b=d}}[a,b+1,c-b(b+1)/2)]-[a,b,c-b(b+1)/2], \end{align*}$$
for
$(d,c)\in ({\mathbb {Z}}/N{\mathbb {Z}})\times ({\mathbb {Z}}/N'{\mathbb {Z}})$
. By Proposition 3.10, it is a subgroup of
$S_{N}$
. Thus, we get a presentation by generators and relations of the homology of
$X^{\prime }_{N}$
.
Corollary 3.11 The map i produces an exact sequence
$$\begin{align*}0\rightarrow R_{N}\rightarrow S_{N}\rightarrow\mathrm H_1(X^{\prime}_N;{\mathbb{Z}}) \rightarrow 0. \end{align*}$$
Remark 3.12 By exchanging the roles of
$\partial ^{+}$
and
$\partial ^{-}$
, it is possible to give a dual presentation of
$\mathrm H_1(X^{\prime }_N;{\mathbb {Z}}) $
. We leave this to the reader.
4 The Heisenberg covering and its models
In this section, we assume N to be odd. Therefore
$N'=N$
.
4.1 Modular functions
Let
$z\in \mathbb {H}$
. For
$q_2=\exp {(\pi i z)}$
, consider the classical
$\lambda $
-function [Reference Murty and Ramakrishnan13]:
$$\begin{align*}\lambda(z)=16 q_2 \prod_{n \geq 1} \left( \frac{1+q_2^{2n}}{1+q_2^{2n-1}}\right)^8, 1-\lambda(z)=\prod_{n \geq 1} \left( \frac{1-q_2^{2n-1}}{1+q_2^{2n-1}}\right)^8. \end{align*}$$
From the above expression, it is clear that
$\lambda (1)=1$
and
$(1-\lambda (1))=0$
. The Nth roots
$$\begin{align*}x:=\sqrt[N]{\lambda}, y:=\sqrt[N]{1-\lambda} \end{align*}$$
define modular units for
$\Phi _{N}$
. We recover thus the familiar model of the Fermat curve.
Since the
$\lambda $
function identifies
${\mathbb {P}}^1-\{0,1,\infty \}$
to
$Y(2)$
, a covering of
${\mathbb {P}}^1-\{0,1,\infty \}$
can be understood as a covering of
$Y(2)$
, i.e., a modular curve.
4.2 Reminder on Fermat curves
The Nth Fermat curve
$F_{N}$
is given by the projective model:
$$\begin{align*}X^N+Y^N=Z^N. \end{align*}$$
Fermat curves and their points at infinity (cusps) are studied extensively by Rohrlich [Reference Rohrlich16, Reference Rohrlich17], Vélu [Reference Vélu18], and Posingies [Reference Posingies15]. In particular, these authors consider the map
$$\begin{align*}\beta_N:F_N \rightarrow {\mathbb{P}}^1 \end{align*}$$
given by
$(X:Y:Z) \rightarrow (X^N:Z^N)$
. The map
$\beta _N$
is of degree
$N^{2}$
. It is ramified only above the points
$0,1,\infty $
. The corresponding ramification points are given by
$a_j=(0:\zeta ^j:1)$
,
$b_j=(\zeta ^j:0:1)$
,
$c_j=(\epsilon \zeta ^j:1:0)$
, for
$j\in {\mathbb {Z}}/N{\mathbb {Z}}$
.
Recall that
$\zeta $
is a primitive Nth root of unity and
$\epsilon $
is a square root of
$\zeta $
. Each of the above points has ramification index N over
${\mathbb {P}}^1$
. For all
$j\in {\mathbb {Z}}/N{\mathbb {Z}}$
, the cusps
$a_j$
,
$b_j$
,
$c_j$
are all defined over the cyclotomic field
$\mathbb {Q}(\mu _N)$
. Among them, only
$a_0$
,
$b_0$
, and
$c_0$
are defined over
$\mathbb {Q}$
.
4.3 The cuspidal subgroup of the Fermat curve
The divisors of following modular functions are given by:
$$\begin{align*}\mathrm{div}(x-\zeta^j)=N b_j-\sum_j c_j, \mathrm{div}(y-\zeta^j)=N a_j-\sum_j c_j, \mathrm{div}(x-\epsilon\xi^j y)=N c_j-\sum_j c_j. \end{align*}$$
Rohrlich [Reference Rohrlich17] has determined the structure of the cuspidal group of the Jacobian of
$F_{N}$
(see also Vélu’s alternative proof and description [Reference Vélu18]). Since every cuspidal divisor on
$F_{N}$
is annihilated by N in the Jacobian, the cuspidal group is a quotient of
${\mathbb {Z}}/N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. The additional relations are given as follows. Recall that N is odd.
Theorem 4.1 (Rohrlich [Reference Rohrlich17])
The group
$\mathcal {P}$
of principal divisors is spanned by the following set:
$$ \begin{align*}\bigg\{\sum_{i=0}^{N-1}[a_{i}]-[P],\sum_{i=0}^{N-1}[b_{i}]-[P],\sum_{i=0}^{N-1}[c_{i}]-[P], \end{align*} $$
$$ \begin{align*}\sum_{i=0}^{N-1}i([a_{i}]-[b_{i}]),\sum_{i=0}^{N-1}i([a_{i}]-[c_{i}]),\sum_{i=0}^{N-1}i^{2}([a_{i}]+[b_{i}]+[c_{i}]-3[P])\bigg\}, \end{align*} $$
where P is any cusp of
$F_{N}$
. Thus, the cuspidal subgroup of the Jacobian of
$F_N$
is a free
${\mathbb {Z}}/N{\mathbb {Z}}$
-module of rank
$3N-7$
.
We set
$$\begin{align*}D_{A}=\sum_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}\{i\}[a_{i}] \end{align*}$$
(resp.
$D_{B}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[b_{i}]$
, resp.
$D_{C}=\sum _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}\{i\}[c_{i}]$
) and
$$\begin{align*}f_{A}=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{\{i\}}. \end{align*}$$
Corollary 4.2 The class of
$D_A$
is of order N in the cuspidal subgroup of the Jacobian of
$F_N$
. Moreover, it is congruent to
$D_B$
and
$D_C$
modulo
$\mathcal {P}$
.
Proof Indeed, the divisor of
$f_A$
is
$ND_A$
. By Rohrlich’s theorem,
$D_A$
is of order N. The congruence of
$D_A$
,
$D_B$
, and
$D_C$
modulo
$\mathcal {P}$
follows from Rohrlich’s relations.
4.4 The covering as a function field extension
By Rohrlich’s theorem, the order of
$D_{A}$
in the cuspidal group is N, therefore an Nth root of
$f_{A}$
defines a cyclic covering
$G\rightarrow F_{N}$
(a provisional notation, since G will be shown to be equal to
$F_N'$
) of degree N. Such a morphism is indeed unramified, since the divisor of
$f_{A}$
belongs to
$N{\mathbb {Z}}[\partial _{\Phi _{N}}]^{0}$
. Since
$D_{A}-D_{B}$
is a principal divisor, exchanging the roles of X and Y would give the same covering. A similar reasoning with respect to
$D_{C}$
holds. The cyclic covering
$G\rightarrow F_{N}$
translates into a covering of Riemann surfaces
$W\rightarrow X_{N}$
.
Consider now the third term
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
in the lower central series of
$\Gamma (2)$
. It is not a subgroup of finite index of
$\Gamma (2)$
, but one can still consider the Riemann surface
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
Proposition 4.3 The covering
$W\rightarrow X_{N}$
factorizes through
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
.
Proof Let
$U\in \Gamma (2)$
and
$V\in [\Gamma (2),\Gamma (2)]]$
. Let g be an Nth root of
$f_{A}$
. One has to prove that g is invariant under
$[U,V]$
, that is,
$g_{|UV}=g_{|VU}$
. Note first that
$y_{|U}=\zeta ^{r}y$
, with
$r\in {{\mathbb {Z}}}$
. One has
$$ \begin{align*}g^{N}_{|U}=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-\zeta^{r}y+\zeta^{i})^{\{i\}}=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i-r})^{\{i\}}=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{\{i+r\}}. \end{align*} $$
Write
$\{i+r\}=\{i\}+r+t$
, with
$t\in N{\mathbb {Z}}$
. Thus, we get
$$ \begin{align*}g^{N}_{|U}=g^N\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{r}\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{t}. \end{align*} $$
The last factor is obviously an Nth power. By the description of Rohrlich of the cuspidal subgroup of
$F_{N}$
, the factor
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
is an Nth power in the function field of
$F_{N}$
. So there exists a function h on
$F_{N}$
, and an integer s such that
$g_{|U}=g\zeta ^{s}h$
. Note that
$h_{|V}=h$
and
$g_{|V}=\zeta ^{q}g$
, with
$q\in {\mathbb {Z}}$
. Therefore, one has
$$ \begin{align*}g_{|UV}=g_{|V}\zeta^{s}h_{|V}=\zeta^{s+q}gh=\zeta^{q}g_{|U}=g_{|VU}.\\[-35pt] \end{align*} $$
Proposition 4.4 Any covering of degree N of the Fermat modular curve
$X_{N}$
that factors through
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, factors through the Heisenberg covering.
Proof Such a covering corresponds to a cyclic quotient of order N of
$\Phi _{N}$
. Denote by
$\Gamma $
the corresponding cocyclic subgroup of
$\Phi _{N}$
. Since the covering is unramified at the cusps,
$\Gamma $
contains the matrices
$A^{N}$
and
$B^{N}$
. Recall that
$\Phi _{N}$
is generated by
$A^{N}$
,
$B^{N}$
and the commutator subgroup of
$\Gamma (2)$
. Since the covering factors through
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
, the group
$\Gamma $
contains
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
. In particular,
$\Gamma $
contains
$[A,C]$
and
$[B,C]$
. Thus, the image of C in
$\Phi _{N}/\Gamma $
is of order N. Consequently,
$\Gamma $
is the group generated by
$[\Gamma (2),[\Gamma (2),\Gamma (2)]]$
,
$A^{N}$
,
$B^{N}$
,
$C^{N}$
.
Corollary 4.5 Let
$\zeta $
be a primitive Nth root of unity in
$\mathbb {Q}(\mu _N)$
. The function
$$\begin{align*}f_{A}'=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{\{i\}} \end{align*}$$
admits an Nth root in the function field of
$F^{\prime }_N$
.
Proof Indeed, the covering of
$F_{N}$
defined by an Nth root of
$f_{A}'$
is cyclic of order N and factorizes through
$X_{[\Gamma (2),[\Gamma (2),\Gamma (2)]]}$
. Consequently, it is
$F^{\prime }_{N}$
.
Let K be the field of fractions of the curve given in the introduction over the complex numbers. In inhomogeneous form, it is generated by the variable X, Y,
$T_{\zeta }$
for every primitive Nth root of unity
$\zeta $
, with the relations
$$ \begin{align*}X^{N}+Y^{N}=1 \end{align*} $$
and, for every primitive Nth root of unity
$\zeta $
(in
$\mathbf {Q}(\mu _{N})$
)
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
Corollary 4.6 The function field of
$F^{\prime }_{N}$
over
$\mathbb {C}$
is isomorphic to K.
Proof Indeed, the function field of
$F^{\prime }_{N}$
is the subfield of K generated by an Nth root of
$f_{A}$
over the function field of
$F_{N}$
. Let
$\zeta '$
be a primitive Nth root of unity. By the preceding corollary,
$T_{\zeta '}$
belongs to K. Thus, all of K is contained in the function field of
$F^{\prime }_{N}$
.
Thus, we have shown that the curve
$F^{\prime }_N$
extends the Riemann surface
$X^{\prime }_N$
.
Corollary 4.7 The Riemann surfaces
$X^{\prime }_N$
and
$F^{\prime }_N({\mathbb {C}})$
are isomorphic.
4.5 The Heisenberg covering
Denote by G the Galois group of the field extension
$K|\mathbb {Q}(X^N)$
. It sits in an exact sequence
$$ \begin{align*}1\rightarrow H_N\rightarrow G\rightarrow ({\mathbb{Z}}/N{\mathbb{Z}})^\times\rightarrow 1 \end{align*} $$
by the transitive action of G on Nth roots of unity, and the fact that the Heisenberg covering is defined over
$\mathbb {Q}(\zeta )$
. Recall that for
$i\in ({\mathbb {Z}}/N{\mathbb {Z}})$
,
$\{i\}$
denotes the representative of i in
$\{-(N-1)/2,\dots , (N-1)/2\}$
.
Proposition 4.8 For
$\sigma \in G$
, there exists u, v,
$s\in ({\mathbb {Z}}/N{\mathbb {Z}})$
and
$r\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
such that
$\sigma (X)=\zeta ^uX$
,
$\sigma (Y)=\zeta ^v(Y)$
,
$\sigma (\zeta )=\zeta ^r$
. For
$\rho $
a representative of r in
${\mathbb {Z}}$
,
$$ \begin{align*}\sigma(T^\rho)=\zeta^sTX^{v}\prod_{i\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^i)^{(\rho\{i/\rho\}-\{i\})/N}. \end{align*} $$
Furthermore,
$(u,v,s,r)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{3}\times ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
characterizes
$\sigma $
.
Proof The first three identities are evident. A simple calculation establishes the last one. Indeed,
$$ \begin{align*}\sigma(T^\rho)^N=\sigma(T^N)^\rho=\sigma(\prod_{i\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^i)^{\{i\}})^\rho=\prod_{i\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-\zeta^vY+\zeta^{\rho i})^{\{i\}\rho}. \end{align*} $$
By factoring
$T^N$
and
$\prod _i \zeta ^{v\{i\}}$
, and replacing the variable i by
$j=\rho i-v$
, one gets
$$ \begin{align*}\sigma(T^\rho)^N=T^N\prod_i\zeta^{v\{i\}}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{j})^{\rho\{(j+v)/\rho\}}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{-\{j\}}. \end{align*} $$
We use
$\prod _i \zeta ^{v\{i\}}=1$
and we get
$$ \begin{align*}\sigma(T^\rho)^N=T^N\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{j})^{\rho\{(j+v)/\rho\}-\{j\}-v}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{v}. \end{align*} $$
Using the identity
$X^N=(1-Y^N)=\prod _{j\in ({\mathbb {Z}}/N{\mathbb {Z}})}(-Y+\zeta ^{j})$
, we get
$$ \begin{align*}\sigma(T^\rho)^N=T^NX^{Nv}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{j})^{\rho\{(j+v)/\rho\}-\{j\}-v}. \end{align*} $$
The desired formula follows by taking Nth roots.
With the notations of the proposition, we note
$\sigma =\sigma _{u,v,r,s}$
. Murty and Rama krishnan note that Deligne showed that
$F^{\prime }_N$
can be defined over
$\mathbb {Q}$
, without giving a reference. We spell out this assertion.
Proposition 4.9 The curve
$F^{\prime }_N$
can be defined over
$\mathbb {Q}$
. More precisely, the surjective map
$G\rightarrow ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
admits the map
$r\mapsto \sigma _{0,0,r,0}$
as a section. Denote by S the corresponding subgroup of G. It acts trivially on Nth roots of unity. Consequently, the field of invariants by S in K is the function field of a curve over
$\mathbb {Q}$
, and defines
$F^{\prime }_N$
over
$\mathbb {Q}$
. The Heisenberg covering
$F^{\prime }_N\rightarrow F_N$
extends also over
$\mathbb {Q}$
.
Proof Group theoretic arguments about the structure of G as an extension imply easily the existence of the section. We will show that our explicit map is indeed a section. Let r,
$r'\in ({\mathbb {Z}}/N{\mathbb {Z}})^\times $
and
$\rho $
and
$\rho '$
be representatives of r and
$r'$
, respectively, in
${\mathbb {Z}}$
. We need to check that
$\sigma _{0,0,r',0}\sigma _{0,0,r,0}=\sigma _{0,0,rr',0}$
, which need to be verified only by application on T, or equivalently on
$T^{\rho \rho '}$
, and on
$\zeta $
. This is trivial for
$\zeta $
. Here is the computation on
$T^{\rho \rho '}$
. We first simplify the formula of the previous proposition
$$ \begin{align*}\sigma_{0,0,r,0}(T^{\rho\rho'})=T^{\rho'}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{(\rho\{j/\rho\}-\{j\})\rho'/N}. \end{align*} $$
Thus, one has
$$ \begin{align*}&\sigma_{0,0,r',0}\sigma_{0,0,r,0}(T^{\rho\rho'})\\&\quad=T\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{(\rho'\{j/\rho'\}-\{j\})/N}\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^{\rho'j})^{(\rho\{j/\rho\}-\{j\})\rho'/N}). \end{align*} $$
A change of variable in the second product of the right-hand side gives
$$\begin{align*}\sigma_{0,0,r',0}\sigma_{0,0,r,0}(T^{\rho\rho'})=T\prod_{j\in ({\mathbb{Z}}/N{\mathbb{Z}})}(-Y+\zeta^j)^{(\rho\rho'\{j/\rho\rho'\}-\{j\})/N}=\sigma_{0,0,rr',0}(T^{\rho\rho'}). \end{align*}$$
4.6 Automorphisms
The group
$({\mathbb {Z}}/N{\mathbb {Z}})^{2}\simeq \Gamma (2)/\Phi _{N}$
acts on
$F_{N}$
:
$(i,j)\in ({\mathbb {Z}}/N{\mathbb {Z}})^{2}$
acts by the rule
$(x,y)\mapsto (\zeta ^{i}x,\zeta ^{j}y)$
. Such an action is defined on
$\mathbb {Q}(\mu _{N})$
. It lifts to an action of
$H_{{\mathbb {Z}}/N{\mathbb {Z}}}\simeq \Gamma (2)/\Phi _{N}'$
on
$F_{N}'$
.
Lemma 4.10 The action of
$H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
on
$F_{N}'$
is defined over
$\mathbb {Q}(\mu _{N})$
.
Proof For
$U\in H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, one needs to check that the action of U on a
$\mathbb {Q}(\zeta )$
-rational function is still
$\mathbb {Q}(\zeta )$
-rational. It suffices to verify this for g, an Nth root of
$f_{A}$
. We repeat a previous calculation and get
$$ \begin{align*}g^{N}_{|U}=g^N\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{r}\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-y+\zeta^{i})^{t}, \end{align*} $$
with
$t\in N{\mathbb {Z}}$
. Both factors
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{r}$
and
$\prod _{i\in {\mathbb {Z}}/N{\mathbb {Z}}}(-y+\zeta ^{i})^{t}$
are Nth power, (of, say,
$g_{1}$
and
$g_{2}$
) in the function field of
$F_{N}$
over
$\mathbb {Q}(\zeta )$
. We thus find that
$g_{|U}$
is equal to
$\zeta ^{p}gg_{1}g_{2}$
, which belongs to the function field of
$X_{N}$
over
$\mathbb {Q}(\zeta )$
.
Remark 4.11 We do not give an explicit algebraic model of the curve
$X^{\prime \prime }_{N}$
. But it can be obtained by taking
$N"$
th roots of the functions whose divisors are
$\sum _{i=0}^{N-1}i^{2}([a_{i}]-[P])\}$
,
$\sum _{i=0}^{N-1}i^{2}([b_{i}]-[P])\}$
and
$\sum _{i=0}^{N-1}i^{2}([c_{i}]-[P])\}$
.
4.7 Regular integral models of Heisenberg curves
We relate the Heisenberg covering to the model given in the introduction. Note that the inhomogeneous version of the projective model is given by
$$ \begin{align*}X^{N}+Y^{N}=1 \end{align*} $$
and, for every primitive Nth root of unity
$\zeta $
(in a fixed cyclotomic extension of
$\mathbf {Q}$
)
$$ \begin{align*}\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j}. \end{align*} $$
We now prove Theorem 1.1 (in the spirit of, e.g., [Reference Curilla3, Proposition 1.1.13]).
Proof We have indeed a scheme of relative dimension
$1$
over
$\mathrm {Spec}({{\mathbb {Z}}}[\mu _{N},1/N])$
. We just have to establish the smoothness. We use the Jacobian criterion (e.g., [Reference Liu8, p. 130, Theorem 2.19]).
Since the Heisenberg covering is obtained by taking the Nth root of a function which does not vanish outside the zero locus of
$XY$
, all points away from
$X=0$
and
$Y=0$
are regular in all characteristics prime to N. It remains to establish the regularity of a point
$P_{\zeta }$
of the form
$(X,Y)=(0,\zeta )$
or
$(X,Y)=(\zeta ,0)$
with
$\zeta $
a primitive Nth root of unity. Suppose
$(X,Y)=(0,\zeta )$
. For points of this form, one has
$T_{\zeta }=0$
. We set
$$\begin{align*}F_{\zeta}=\prod_{j=1}^{(N-1)/2}(Y-\zeta^{-j})^{j}T_{\zeta}^{N}-\prod_{j=1}^{(N-1)/2}(Y-\zeta^{j})^{j} \end{align*}$$
and compute the partial derivative at
$P_{\zeta }$
. One obtains
$$\begin{align*}\frac{\partial F_{\zeta}}{\partial Y}(P_{\zeta})=- \prod_{j=2}^{(N-1)/2}(\zeta-\zeta^{j})^{j}, \end{align*}$$
which is a cyclotomic unit that belongs to
$\mathbf {Z}[\mu _{N},1/N]^{\times }$
. Thus, the Jacobian matrix is nonzero over any fiber in characteristic prime to N. This is sufficient to establish the regularity of
$P_{\zeta }$
over
$\mathrm {Spec}(\mathbf {Z}[\mu _{N},1/N])$
since the structural morphism is of relative dimension
$1$
. This reasoning applies to the zero locus of Y, by exchanging the roles of X and Y.
4.8 Cusps
The term cusp refers to the cusps of the modular curve
$X_\Gamma $
attached to a subgroup
$\Gamma $
of
$\Gamma (2)$
. These points are not intrinsic to the corresponding algebraic curves. In the cases of interest to us, we have a morphism
$X_N\rightarrow X(2)$
, given by the function
$x^N$
. Thus, the cusps of
$F_N$
are the
$3N$
points above the points
$0$
,
$1$
, and
$\infty $
described above.
Since the morphism
$F^{\prime }_N\rightarrow F_N$
is unramified, the modular curve
$F^{\prime }_N$
possesses
$3N^2$
cusps.
Proposition 4.12 If N is prime to
$3$
, the cusps of
$F^{\prime }_N$
are defined over
$\mathbb {Q}(\zeta )$
. If
$3$
divides N, the cusps of
$F^{\prime }_N$
are defined over the cyclotomic field generated by the
$3N$
th roots of unity.
Proof Let a be a cusp of
$F^{\prime }_{N}$
above
$a_{0}$
. It is defined over the field generated by
$g(a)$
and
$\mathbb {Q}(\zeta )$
, where g is an Nth root of
$f_{A}$
. One has
$$ \begin{align*}f_{A}(a_{0})=\prod_{i\in{\mathbb{Z}}/N{\mathbb{Z}}}(-1+\zeta^{i})^{\{i\}}=\prod_{i=1}^{(N-1)/2}\frac{(-1+\zeta^{i})^{i}}{(-1+\zeta^{-i})^{i}}=\prod_{i=1}^{(N-1)/2}(-\zeta^{i})^{i}. \end{align*} $$
Thus, we get
$$ \begin{align*}f_{A}(a_{0})=(-1)^{\sum_{i=1}^{(N-1)/2}i}\zeta^{\sum_{i=1}^{(N-1)/2}i^2}=(-1)^{(N^2-1)/8}\zeta^{(N-1)(N+1)N/24}, \end{align*} $$
which is a sixth root of unity.
Suppose N is prime to
$3$
. Then
$g(a)$
is an Nth root of unity, up to sign. Since the group
$H_{N}$
acts transitively on the cups above
$\infty $
, and its action is
$\mathbb {Q}(\zeta )$
-rational, we deduce that all the cusps above
$\infty $
are defined over
$\mathbb {Q}(\zeta )$
. A similar reasoning apply to the cusps above
$0$
, and above
$1$
.
A similar reasoning applies when
$3$
divides N. Indeed,
$g(a)$
is a
$3N$
th root of unity, up to sign.
The cusps of
$F^{\prime }_N$
above the cusp
$\infty $
(resp.
$0$
, resp.
$1$
) of
$X(2)$
coincide with the classes
$\Gamma \backslash \Gamma (2)\infty $
(resp.
$\Gamma \backslash \Gamma (2)0$
, resp.
$\Gamma \backslash \Gamma (2)1$
), which in turn can be identified with the double classes
$\Gamma \backslash \Gamma (2)/A^{{\mathbb {Z}}}$
(resp.
$\Gamma \backslash \Gamma (2)/B^{{\mathbb {Z}}}$
, resp.
$\Gamma \backslash \Gamma (2)/(AB^{-1})^{{\mathbb {Z}}}$
).
4.9 About the Manin–Drinfeld principle for
$F^{\prime }_3$
Recall that
$g_{3}=1$
and observe that
$F^{\prime }_{3}$
has 27 cusps. Fix one cusp
$P_{0}$
of
$F^{\prime }_{3}$
, which becomes thus an elliptic curve
$(F^{\prime }_{3}, P_{0})$
. Since a cyclic group of order
$3$
acts on
$F^{\prime }_{3}$
and stabilizes
$P_{0}$
, the elliptic curve
$(F^{\prime }_{3}, P_{0})$
admits an automorphism of order
$3$
. Thus, the j-invariant of
$(F^{\prime }_{3}, P_{0})$
is
$0$
.
Proposition 4.13 Divisors supported on the cusps of
$F^{\prime }_{3}$
above
$\infty $
(resp.
$0$
, resp.
$1$
) are of order dividing
$3$
in the Jacobian of
$F^{\prime }_{3}$
. Furthermore, cuspidal divisors of degree
$0$
are torsion in the Jacobian of
$F^{\prime }_3$
, and of order dividing
$9$
.
Proof Let X be a compact connected Riemann surface of genus
$1$
. Let J be the Jacobian of X. Recall the exact sequence
$$ \begin{align*}0\rightarrow J(\mathbf{C})\rightarrow \mathrm{Aut}(X)\rightarrow \mathrm{Aut}(J)\rightarrow 0, \end{align*} $$
where
$\mathrm {Aut}$
denotes the automorphisms over
$\mathbf {C}$
. The first map associates to the class of a divisor D the translation by D in X.
For
$X=F^{\prime }_{3}$
, the group
$\mathrm {Aut}(J)$
is cyclic of order
$6$
. One gets a group homomorphism
$H_{\mathbf {Z}/3\mathbf {Z}}\rightarrow \mathrm {Aut}(J)$
, whose kernel is of order
$9$
, and therefore isomorphic to
$(\mathbf { Z}/3\mathbf {Z})^{2}$
. Since this kernel identifies to a subgroup of the one dimensional complex torus
$J(\mathbf {C})$
, the latter subgroup is
$J(\mathbf {C})[3]$
. We have proved that the orbit of any cups Q by
$H_{\mathbf {Z}/3\mathbf {Z}}$
contains
$Q+J(\mathbf {C})[3]$
. But these sets are both of cardinality
$9$
, and are therefore equal. Since
$H_{\mathbf {Z}/3\mathbf {Z}}$
acts transitively on the cusps above
$\infty $
(resp.
$0$
, resp.
$1$
), the first statement of the proposition is proved.
About the second statement, it is sufficient to prove this for a divisor of the form
$(\alpha )-(\beta ),$
where
$\alpha $
and
$\beta $
are cusps of
$F^{\prime }_3$
not above the same point of
$\{0,1,\infty \}$
. Without loss of generality, say they are above
$0$
and
$\infty $
, respectively. Let a and b be the cusps of
$F_3$
below
$\alpha $
and
$\beta $
, respectively. We have
$$\begin{align*}3((\alpha)-(\beta))=(3(\alpha)-\sum_{\alpha'}(\alpha'))+(\sum_{\alpha'}(\alpha')-\sum_{\beta'}(\beta'))+(\sum_{\beta'}(\beta')-3(\beta)), \end{align*}$$
where
$\alpha '$
(resp.
$\beta '$
) runs through the cusps of
$F^{\prime }_3$
above a (resp. b). By the first statement of the proposition and the torsion properties of the cuspidal subgroup of the
$F_3$
, each of the three terms of the right-hand side is of order dividing
$3$
.
Recall that the dessin for
$X^{\prime }_{N}$
is a graph with the following additional structure: the vertices are bicolored (white and black) and the of set edges attached to any given vertex are endowed with a cyclic ordering (a transitive action of
${\mathbb {Z}}$
). The vertices are the cusps of
$X^{\prime }_{N}$
above
$0$
and
$\infty $
. The edges form the coset
$\Phi ^{\prime }_{N}\backslash \Gamma (2)\simeq H_{{\mathbb {Z}}/N{\mathbb {Z}}}$
, which is in bijection with
$({\mathbb {Z}}/N{\mathbb {Z}})^{3}$
. the edge associated with
$\Phi ^{\prime }_{N}g$
has extremities
$\Phi ^{\prime }_{N}g0$
and
$\Phi ^{\prime }_{N}g\infty $
. The cyclic ordering of the edges attached to the vertices
$\Phi ^{\prime }_{N}g0$
(resp.
$\Phi ^{\prime }_{N}g\infty $
) is given by the action of B (resp.
$A^{-1}$
). To sum up, the dessin can be drawn on
$X^{\prime }_{N}$
.
To be more concrete, each edge is in bijection with
${\mathbb {Z}}/N{\mathbb {Z}}\times {\mathbb {Z}}/N'{\mathbb {Z}}\times {\mathbb {Z}}/N{\mathbb {Z}}$
, via the map
$\Phi ^{\prime }_{N}A^{a}C^{c}B^{b}\mapsto (a,c,b)$
. The edge thus labeled
$(a,c,b)$
is connected to the edge labeled
$(a,c,b+1)$
via a black vertex (cusp above
$0$
) and the edge labeled
$(a,c,b)$
is connected to the edge labeled
$(a-1,c-ab,b)$
via a white vertex (cusp above
$\infty $
). The line segments represent the arcs on
$X^{\prime }_3$
above the geodesic arc from
$0$
to
$\infty $
in the upper half-plane.
We illustrate all this for
$N=3$
. In that case, the genus of
$X^{\prime }_{3}$
is equal to
$1$
. According to these rules, the drawing (dessin) for
$X_3'$
is given as follows.
As the group
$\Phi _{3}$
is not a congruence subgroup [Reference Phillips and Sarnak14],
$\Phi ^{\prime }_{3}$
is a fortiori not a congruence subgroup. The latter fact can be derived alternately from Wolfart’s criterion and an examination of the dessin. Indeed, the width of the each cusps is equal to
$6$
and
$[\Gamma (2):\Phi ^{\prime }_3]=27$
. Wolfart’s criterion, to check that
$\Phi ^{\prime }_3$
is a congruence subgroup or not it is enough to check
$\Gamma (6) \subset \Phi ^{\prime }_3 \subset \Gamma (2)$
. However,
$[\Gamma (2):\Gamma (6)]=144$
is not divisible by the index
$27$
.
4.10 About the failure of the Manin–Drinfeld principle for
$F^{\prime }_5$
Suppose
$N=5$
. We show that the Manin–Drinfeld theorem fails for the Heisenberg covering
${\mathcal {F}}^{\prime }_5$
of
${\mathcal {F}}_5$
. Consider the scheme
${\mathcal {C}}_5$
over
$\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _{5},1/5])$
given by the system of equations
$$ \begin{align*}T_\zeta^5=\frac{(-Y+\zeta)(-Y+\zeta^2)^2}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}, \end{align*} $$
where
$\zeta $
runs through the primitive fifth roots of unity in
$\mathbb {Q}(\mu _{5})$
. It is smooth, as can be shown by applying the Jacobian criterion. One has an obvious morphism of schemes
${\mathcal {F}}^{\prime }_5\rightarrow {\mathcal {C}}_5$
.
Denote by
$C_{5}$
the generic fiber of
${\mathcal {C}}_5$
. Over
$\mathbb {C}$
,
$C_5$
identifies to a modular curve as follows. Consider the morphism
$\bar \Gamma (2)\rightarrow H_{5,5,5}$
and the inverse image
$\Gamma '$
of the subgroup of
$H_{5,5,5}$
generated by B. Then
$\Gamma '$
defines a corresponding modular curve isomorphic to the Riemann surface
$C_5(\mathbb {C})$
.
The curve
$C_{5}$
possesses
$19$
cusps, given by the following planar coordinates
$(Y,T_{\zeta })$
:
$(0,\epsilon )$
,
$(\infty , \epsilon )$
,
$(1, -\delta )$
,
$(\zeta ,0)$
,
$(\zeta ^2,0)$
,
$(\zeta ^{-1},\infty )$
,
$(\zeta ^{-2},\infty )$
, where
$\epsilon $
and
$\delta $
run through the fifth roots of unity. Set
$T=T_{\zeta }$
. The function fields of
$F^{\prime }_{5}$
and
$C_{5}$
are
$\mathbf {Q}(\zeta ,X,Y,T)$
and
$\mathbf {Q}(\zeta ,Y,T)$
, respectively.
The obvious morphism
$\pi $
:
$F^{\prime }_5\rightarrow C_5$
sends the cusps of
$F^{\prime }_5$
to the cusps of
$C_5$
. We show that
$C_5$
does not satisfy the Manin–Drinfeld principle. Since
${\mathcal {C}}_5$
is smooth, the Jacobian of
$C_5$
extends to an abelian scheme
${\mathcal {J}}_5$
over
$\operatorname {{\mathrm {Spec}}}(\mathbf {Z}[\mu _5,1/5])$
.
Proposition 4.14 There exists a divisor of infinite order supported on the cusps of
$C_{5}$
.
Proof We suppose that all cuspidal divisors are torsion in
$C_{5}$
. Our proof is organized around the following calculation. One has
$$ \begin{align} T^5+1=\frac{(1-Y)(2Y^2+(2-2(\zeta^2+\zeta^{-2})-\zeta-\zeta^{-1})Y+2)}{(-Y+\zeta^{-1})(-Y+\zeta^{-2})^2}. \end{align} $$
Let
$y_1$
and
$y_2$
be the roots of the polynomial
$2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
. Let
$\zeta _1$
be a fifth root of unity in
$\mathbf {Z}[\mu _5]$
. Consider the function
$T+\zeta _1$
, which divides
$T^5+1$
. The divisor of the function
$T+\zeta _1$
is (in terms of planar coordinates for
$(Y,T)$
):
$(1,-\zeta _1)+(y_1,-\zeta _1)+(y_2,-\zeta _1)-D$
, where
$D=(\zeta ^{-1},\infty )+2(\zeta ^{-2},\infty )$
. Apparently fortuitously, this divisor is cuspidal in the fibers at
$11$
and at
$2$
of
$C_{5}$
.
Lemma 4.15 Let
$\zeta _1$
and
$\zeta _2$
be distinct primitive fifth roots of unity in
${\mathbb {Z}}[\mu _5]$
. The divisors
$3(1,\zeta _1)-3(1,\zeta _2)$
and
$3(1,\zeta _1)-D$
are principal in any fiber above
$11$
of
$C_5$
.
Proof In characteristic
$11$
, the polynomial
$2Y^2+(2-2(\zeta ^2+\zeta ^{-2})-\zeta -\zeta ^{-1})Y+2$
has the providential property of having a double root equal to
$1$
. Therefore, the divisor of the function
$T+\zeta _1$
over
$\mathbb {F}_{11}$
is cuspidal and equal to
$3(1,\zeta _1)-D$
. It follows that the function
$(T+\zeta _1)/(T+\zeta _2)$
has divisor
$3(1,\zeta _1)-3(1,\zeta _2)$
.
We return to the proof of the proposition. By our Manin–Drinfeld assumption in
$C_{5}$
, the divisor
$3(1,\zeta _1)-D$
is torsion in the Jacobian of
$C_{5}$
. It extends to a torsion point of
${\mathcal {J}}_5$
, whose order is determined in any special fiber at a prime
$\pi $
of residual characteristic p, provided
$p-1>e$
, where e is the ramification index at
$\pi $
of the extension
${\mathbb {Q}}(\mu _5)|{\mathbb {Q}}$
[Reference Mazur11]. This applies for any prime except perhaps
$p=2$
and
$p=5$
. The calculation for
$p=11$
ensures that the divisors
$3(1,\zeta _1)-3(1,\zeta _2)$
and
$3(1,\zeta _1)-D$
are principal in
$C_{5}$
.
Therefore, those divisors are principal in any special fiber of
${\mathcal {C}}_5$
. Consider any fiber
$\bar {C}$
above
$2$
of
$C_{5}$
. In that fiber, the function
$T-\zeta =T+\zeta $
has divisor, in view of Equation (4.1),
$(0,\zeta )+(1,\zeta )+(\infty ,\zeta )-D_{\zeta }$
, which is principal. Thus, by taking
$\zeta _{1}=\zeta $
, the divisor
$$\begin{align*}(3(1,\zeta)-D_{\zeta})-((0,\zeta)+(1,\zeta)+(\infty,\zeta)-D_{\zeta})=2(1,\zeta)-(0,\zeta)-(1,\zeta) \end{align*}$$
is principal in
$\bar C$
. Thus, there exists f:
${\bar C}\rightarrow {\mathbb {P}}^{1}$
of degree
$2$
. So
$\bar {C}$
is hyperelliptic. The principality of the divisor
$3(1,\zeta _1)-3(1,\zeta _2)$
ensures that there is a degree
$3$
morphism
$\bar C\rightarrow {\mathbb {P}}^{1}$
. By Castelnuovo–Severi-type inequalities, this imposes that the genus of
$\bar {C}$
is
$\le 2$
. But the genus of
$\bar C$
equals the genus of
$C_{5}$
; it is equal to
$6$
and we have reached a contradiction.
