Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-09T02:17:19.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for Polynomials with a Prescribed Zero

Published online by Cambridge University Press:  20 November 2018

Abdul Aziz
Abdul Aziz*
Affiliation:
University of Kashmir, Kashmir, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If P(z) is a polynomial of degree n, then the inequality

1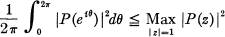

is trivial. It was asked by Callahan [1], what improvement results from supposing that P(z) has a zero on |z| = 1 and he answered the question by showing that if P( l ) = 0, then

2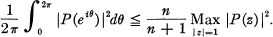

Donaldson and Rahman [3] have shown that if P(z) is a polynomial of degree n such that P(β) = 0 where β is an arbitrary non-negative number, then

3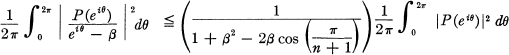

whereas if the polynomial P(z) is such that P(l) = 0, then [4]

4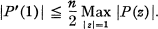

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 737 - 740
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Callahan, F. P., Jr., An extremal problem for polynomials, Proc. Amer. Math. Soc. 10 (1959), 754–755.Google Scholar
2. Van Der Corput, J. G. and Visser, C., Inequalities concerning polynomials and trigonometric polynomials, Nederl. Akad Wetensch., Proc. 49 (1946), 383–392.Google Scholar
3. Donaldson, J. D. and Rahman, Q. I., Inequalities for polynomials with a prescribed zero, Pacific J. Math. 41 (1972), 375–378.Google Scholar
4. Rahman, Q. I. and Mohammad, Q. G., Remarks on Schwarz’ slemma, Pacific J. Math. 28 (1967), 139–142.Google Scholar
5. Szasz, O., Elementare extremal problème uber nicht negative trigonometrische polynôme, Bayer, S. B.. Akad. Wiss. Math. Phys. Kl. (1927), 185–196.Google Scholar