Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-08T14:40:08.994Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotropic Immersions

Published online by Cambridge University Press:  20 November 2018

Sadahiro Maeda
Sadahiro Maeda*
Affiliation:
Kumamoto Institute of Technology, Kumamoto, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, Ferus ([5], [6]) classified connected Riemannian manifolds with parallel second fundamental form in a real space form of constant curvature 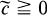. In this paper we may restrict our attention to isotropic submanifolds with parallel second fundamental form in the Euclidean sphere Sm(k) of constant curvature k. Due to Ferus, we find that an isotropic submanifold with parallel second fundamental form in Sm is locally congruent to one of compact symmetric spaces of rank one and the immersion is locally equivalent to the second or the first standard immersion according as M is a sphere or not. In Section 2, we characterize the first standard immersion of a complex projective space into a sphere in terms of isotropic immersions.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 416 - 430
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Chen, B. Y. and Ogiue, K., On totally real submanifolds, Trans. Amer. Math. Soc. 193 (1974), 257–266.Google Scholar
2. Chen, B. Y. and Ogiue, K., Two theorems on Kaehler manifolds, Michigan Math. J. 21 (1974), 28–229.Google Scholar
3. Chen, B. Y. and Vanhecke, L., Differential geometry of geodesic spheres, J. Reine Angew. Math. 325 (1981), 28–67.Google Scholar
4. Egiri, N., Totally real minimal immersions of n-dimensional real space forms into n-dimensional complex space forms, Proc. Amer. Math. Soc. 84 (1982), 243–246.Google Scholar
5. Ferus, D., Immersions with parallel second fundamental form, Math. Z. 140 (1974), 87–93.Google Scholar
6. Ferus, D., Symmetric submanifolds of Euclidean space, Math. Ann. 247 (1980), 81–93.Google Scholar
7. Kleinjohann, N. and Walter, R., Nonnegativity of the curvature operator and isotropy for isometric immersions, Math. Z. 181 (1982), 129–142.Google Scholar
8. Naitoh, H., Isotropic submanifolds with parallel second fundamental form in Pm(c), Osaka J. Math. 18 (1981), 427–464.Google Scholar
9. Nakagawa, H. and Itoh, T., On isotropic immersions of space forms into a sphere, Proc. of Japan-United States Seminar on minimal submanifolds, including Geodesies (1978).Google Scholar
10. O'Neill, B., Isotropic and Kaehler immersions, Can. J. Math. 17 (1965), 905–915.Google Scholar
11. Nomizu, K., A characterization of the Veronese varieties, Nagoya Math. J. 60 (1976), 181–188.Google Scholar
12. Nomizu, K. and Yano, K., On circles and spheres in Riemannian geometry, Math. Ann. 210 (1974), 163–170.Google Scholar
13. Sakamoto, K., Planar geodesic immersions, Tohoku Math. J. 29 (1977), 25–56.Google Scholar
14. Tashiro, Y. and Tachibana, S., On Fubinian and C-Fubinian manifolds, Kodai Math. Sem. Rep. 75 (1963), 176–183.Google Scholar
15. Yano, K., Kon, M. and Ishihara, I., Anti-invariant submanifolds with flat normal connection, J. Diff. Geom. 13 (1978), 577–588.Google Scholar