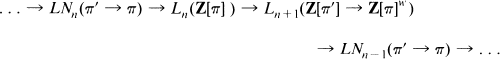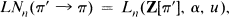Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Muranov, Yu V
and
Repovs, D
1997.
Groups of obstructions to surgery and splitting for a manifold pair.
Sbornik: Mathematics,
Vol. 188,
Issue. 3,
p.
449.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Реповш, Душан
and
Repovs, Dusan
1997.
Группы препятствий к перестройкам и расщеплениям для пары многообразий.
Математический сборник,
Vol. 188,
Issue. 3,
p.
127.
Muranov, Yu. V.
and
Repovš, D.
1998.
Surgery of closed manifolds with dihedral fundamental group.
Mathematical Notes,
Vol. 64,
Issue. 2,
p.
202.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Реповш, Душан
and
Repovs, Dusan
1998.
Перестройки замкнутых многообразий с диэдральной фундаментальной группой.
Математические заметки,
Vol. 64,
Issue. 2,
p.
238.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Хэмблтон, И
and
Hambleton, Ian
1999.
Проективные группы препятствий к расщеплению вдоль односторонних подмногообразий.
Математический сборник,
Vol. 190,
Issue. 10,
p.
65.
Muranov, Yu V
and
Hambleton, I
1999.
Projective splitting obstruction groups for one-sided submanifolds.
Sbornik: Mathematics,
Vol. 190,
Issue. 10,
p.
1465.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Реповш, Душан
and
Repovs, Dusan
2001.
Группы $LS$ и морфизмы квадратичных расширений.
Математические заметки,
Vol. 70,
Issue. 3,
p.
419.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Реповш, Душан
and
Repovs, Dusan
2002.
Геометрические свойства спектральной последовательности теории перестроек.
Успехи математических наук,
Vol. 57,
Issue. 6,
p.
191.
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Реповш, Душан
Repovs, Dusan
Спаггиари, Фульвиа
and
Spaggiari, Fulvia
2003.
Перестройка троек многообразий.
Математический сборник,
Vol. 194,
Issue. 8,
p.
139.
Mahmoudi, M. G.
2005.
Hermitian forms and the u-invariant.
manuscripta mathematica,
Vol. 116,
Issue. 4,
p.
493.
Grenier-Boley, N.
and
Mahmoudi, M.G.
2005.
EXACT SEQUENCES OF WITT GROUPS.
Communications in Algebra,
Vol. 33,
Issue. 4,
p.
965.
Jimenez, Rolando
Muranov, Yu. V.
and
Repovš, Dušan
2008.
Splitting along a submanifold pair.
Journal of K-Theory,
Vol. 2,
Issue. 2,
p.
385.
Бак, Энтони
Bak, Anthony
Муранов, Юрий Владимирович
and
Muranov, Yury Vladimirovich
2008.
Расщепление простой гомотопической эквивалентности вдоль подмногообразия с фильтрацией.
Математический сборник,
Vol. 199,
Issue. 6,
p.
3.
Cavicchioli, Alberto
Muranov, Yuri V.
and
Spaggiari, Fulvia
2009.
Surgery on pairs of closed manifolds.
Czechoslovak Mathematical Journal,
Vol. 59,
Issue. 2,
p.
551.
Кавиччоли, Альберто
Cavicchioli, Alberto
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Муранов, Юрий Владимирович
Muranov, Yury Vladimirovich
Спаггиари, Фульвиа
Spaggiari, Fulvia
Хегенбарт, Фридрих
and
Hegenbarth, Friedrich
2009.
Об итерированных инвариантах Браудера - Ливси.
Математические заметки,
Vol. 86,
Issue. 2,
p.
213.
Cavicchioli, Alberto
Muranov, Yuri V.
and
Spaggiari, Fulvia
2009.
Assembly maps and realization of splitting obstructions.
Monatshefte für Mathematik,
Vol. 158,
Issue. 4,
p.
367.
Cavicchioli, A.
Muranov, Yu. V.
Spaggiari, F.
and
Hegenbarth, F.
2009.
On iterated Browder-Livesay invariants.
Mathematical Notes,
Vol. 86,
Issue. 1-2,
p.
196.
Hegenbarth, F.
Muranov, Yu. V.
and
Repovš, D.
2013.
Browder-Livesay Filtrations and the Example of Cappell and Shaneson.
Milan Journal of Mathematics,
Vol. 81,
Issue. 1,
p.
79.
Akhmet'ev, Petr Mikhailovich
and
Muranov, Yury Vladimirovich
2023.
Об арф-инвариантах в коразмерности 1 в группе Уолла диэдральной группы.
Математический сборник,
Vol. 214,
Issue. 5,
p.
3.
Akhmet'ev, Petr Mikhailovich
and
Muranov, Yury Vladimirovich
2023.
Arf invariants of codimension one in a Wall group of the dihedral group.
Sbornik: Mathematics,
Vol. 214,
Issue. 5,
p.
613.