Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-01T21:31:43.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Marcinkiewicz Multipliers and Lipschitz Spaces on Heisenberg Groups

Part of: Harmonic analysis in several variables Abstract harmonic analysis

Published online by Cambridge University Press:  09 January 2019

Yanchang Han ,
Yongsheng Han ,
Ji Li  and
Chaoqiang Tan
Yanchang Han
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou, 510631, China Email: 20051017@m.scnu.edu.cn
Yongsheng Han
Affiliation:
Department of Mathematics, Auburn University, Auburn, AL 36849, USA Email: hanyong@auburn.edu
Ji Li*
Affiliation:
Department of Mathematics, Macquarie University, Sydney NSW 2109, Australia Email: ji.li@mq.edu.au
Chaoqiang Tan
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515041, China Email: cqtan@stu.edu.cn
*
*Ji Li is the corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Marcinkiewicz multipliers are 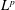$L^{p}$ bounded for $1<p<\infty$ on the Heisenberg group 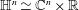$\mathbb{H}^{n}\simeq \mathbb{C}^{n}\times \mathbb{R}$ (Müller, Ricci, and Stein). This is surprising in the sense that these multipliers are invariant under a two parameter group of dilations on 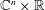$\mathbb{C}^{n}\times \mathbb{R}$, while there is no two parameter group of automorphic dilations on 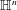$\mathbb{H}^{n}$. The purpose of this paper is to establish a theory of the flag Lipschitz space on the Heisenberg group 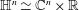$\mathbb{H}^{n}\simeq \mathbb{C}^{n}\times \mathbb{R}$ that is, in a sense, intermediate between that of the classical Lipschitz space on the Heisenberg group 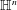$\mathbb{H}^{n}$ and the product Lipschitz space on 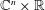$\mathbb{C}^{n}\times \mathbb{R}$. We characterize this flag Lipschitz space via the Littlewood–Paley theory and prove that flag singular integral operators, which include the Marcinkiewicz multipliers, are bounded on these flag Lipschitz spaces.

Keywords

Heisenberg groupMarcinkiewicz multiplierflag singular integralflag Lipschitz spacereproducing formuladiscrete Littlewood–Paley analysis

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory 42B35: Function spaces arising in harmonic analysis 43A17: Analysis on ordered groups, $H^p$-theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 3 , June 2019 , pp. 607 - 627
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The first author is supported by National Natural Science Foundation of China (Grant No. 11471338) and Guangdong Province Natural Science Foundation (Grant No. 2017A030313028); The third author is supported by the Australian Research Council under Grant No. ARC-DP160100153 and by Macquarie University Seeding Grant.

References

Carleson, L., A counterexample for measures bounded on H p for the bidisc. Mittag-Leffler Report, 7, 1974.Google Scholar
Cheeger, J., Differentiability of Lipschitz functions on metric measure spaces . Geom. Funct. Anal. 9(1999), no. 3, 428–517. https://doi.org/10.1007/s000390050094.Google Scholar
Chang, S-Y. A., Carleson measures on the bi-disc . Ann. of Math. 109(1979), 613–620. https://doi.org/10.2307/1971229.Google Scholar
Chang, S-Y. A. and Fefferman, R., Some recent developments in Fourier analysis and H p theory on product domains . Bull. Amer. Math. Soc. 12(1985), 1–43. https://doi.org/10.1090/S0273-0979-1985-15291-7.Google Scholar
Chang, S-Y. A. and Fefferman, R., The Calderón–Zygmund decomposition on product domains . Amer. J. Math. 104(1982), 455–468. https://doi.org/10.2307/2374150.Google Scholar
Chang, S-Y. A. and Fefferman, R., A continuous version of duality of H 1 with BMO on the bidisc . Ann. of Math. 112(1980), 179–201. https://doi.org/10.2307/1971324.Google Scholar
Fefferman, C. and Stein, E. M., H p spaces of several variables . Acta Math. 129(1972), 137–193. https://doi.org/10.1007/BF02392215.Google Scholar
Fefferman, R., Multi-parameter Fourier analysis . Beijing Lectures in Harmonic Analysis, Ann. of Math. Stud., 112, Princeton University Press, Princeton, NJ, 1986, pp. 47–130.Google Scholar
Fefferman, R., Harmonic analysis on product spaces . Ann. of Math. 126(1987), 109–130. https://doi.org/10.2307/1971346.Google Scholar
Fefferman, R., Multiparameter Calderón–Zygmund theory . In: Harmonic analysis and partial differential equations (Chicago, IL, 1996), Chicago Lectures in Math., Univ. Chicago Press, Chicago, IL, 1999, pp. 207–221.Google Scholar
Fefferman, R., Singular integrals on product spaces . Adv. Math. 45(1982), 117–143. https://doi.org/10.1016/S0001-8708(82)80001-7.Google Scholar
Geller, D. and Mayeli, A., Continuous wavelets and frames on stratified Lie groups . I. J. Fourier Anal. Appl. 12(2006), 543–579. https://doi.org/10.1007/s00041-006-6002-4.Google Scholar
Gundy, R. and Stein, E. M., H p theory for the polydisk . Proc. Nat. Acad. Sci. 76(1979), no. 3, 1026–1029. https://doi.org/10.1073/pnas.76.3.1026.Google Scholar
Han, Y., Lu, G., and Sawyer, E., Flag Hardy spaces and Marcinkiewicz multipliers on the Heisenberg group . Anal. PDE 7(2014), no. 7, 1465–1534. https://doi.org/10.2140/apde.2014.7.1465.Google Scholar
Harboure, E., Salinas, O., and Viviani, B., Boundedness of the fractional integral on weighted Lebesgue and Lipschitz spaces . Trans. Amer. Math. Soc. 349(1997), no. 1, 235–255. https://doi.org/10.1090/S0002-9947-97-01644-9.Google Scholar
Jansono, S., Taibleson, M., and Weiss, G., Elementary characterizations of the Morrey-Campanato spaces . In: Harmonic analysis (Cortona, 1982), Lecture Notes in Math., 992, Springer, Berlin, 1983, pp. 101–114.Google Scholar
Journé, J. L., Calderón–Zygmund operators on product spaces . Rev. Mat. Iberoamericana 1(1985), 55–91. https://doi.org/10.4171/RMI/15.Google Scholar
Journé, J. L., A covering lemma for product spaces . Proc. Amer. Math. Soc. 96(1986), 593–598. https://doi.org/10.1090/S0002-9939-1986-0826486-9.Google Scholar
Journé, J. L., Two problems of Calderón–Zygmund theory on product spaces . Ann. Inst. Fourier(Grenoble) 38(1988), 111–132. https://doi.org/10.5802/aif.1125.Google Scholar
Krantz, S. G., Geometric Lipschitz spaces and applications to complex function theory and nilpotent groups . J. Funct. Anal. 34(1979), no. 3, 456–471. https://doi.org/10.1016/0022-1236(79)90087-9.Google Scholar
Krantz, S. G., Lipschitz spaces on stratified groups . Trans. Amer. Math. Soc. 269(1982), no. 1, 39–66. https://doi.org/10.1090/S0002-9947-1982-0637028-6.Google Scholar
Madych, W. R. and Rivière, N. M., Multiplies of the Hölder classes . J. Funct. Anal. 21(1976), no. 4, 369–379. https://doi.org/10.1016/0022-1236(76)90032-X.Google Scholar
Müller, D., Ricci, F., and Stein, E. M., Marcinkiewicz multipliers and multi-parameter structure on Heisenberg(-type) groups. I . Invent. Math. 119(1995), 119–233. https://doi.org/10.1007/BF01245180.Google Scholar
Müller, D., Ricci, F., and Stein, E. M., Marcinkiewicz multipliers and multi-parameter structure on Heisenberg(-type) groups. II . Math. Z. 221(1996), 267–291. https://doi.org/10.1007/BF02622116.Google Scholar
Nagel, A., Ricci, F., and Stein, E. M., Singular integrals with flag kernels and analysis on quadratic CR manifolds . J. Func. Anal. 181(2001), 29–118. https://doi.org/10.1006/jfan.2000.3714.Google Scholar
Nagel, A., Ricci, F., Stein, E. M., and Wainger, S., Singular integrals with flag kernels on homogeneous groups. I . Rev. Mat. Iberoam. 28(2012), 631–722. https://doi.org/10.4171/RMI/688.Google Scholar
Nagel, A., Ricci, F., Stein, E. M., and Wainger, S., Algebras of singular integral operators with kernels controlled by multiple norms. arxiv:1511.05702.Google Scholar
Phong, D. H. and Stein, E. M., Some further classes of pseudo-differential and singular integral operators arising in boundary valve problems. I. composition of operators . Amer. J. Math. 104(1982), 141–172. https://doi.org/10.2307/2374071.Google Scholar
Pipher, J., Journé’s covering lemma and its extension to higher dimensions . Duke Math. J. 53(1986), 683–690. https://doi.org/10.1215/S0012-7094-86-05337-8.Google Scholar
Stein, E. M., Singular integral and differentiability properties of functions. Princeton Univ. Press 30(1970).Google Scholar
Stein, E. M., Singular integrals and estimates for the Cauchy-Riemann equations . Bull. Amer. Math. Soc. 79(1973), no. 2, 440–445. https://doi.org/10.1090/S0002-9904-1973-13205-7.Google Scholar