Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-08T20:47:54.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Motions of Matrix Rings

Published online by Cambridge University Press:  20 November 2018

Roy F. Keller
Roy F. Keller*
Affiliation:
University of Missouri, Columbia, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Metric spaces in which the distances are not real numbers have been studied by several people (2, 3, 4, 7, 9). Any ring R together with a mapping, X —> ϕ(X), of R into a lattice A with 0 and 1 satisfying

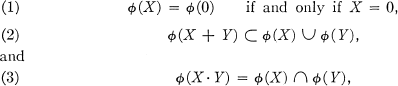
is called a "lattice-valued ring," where the operations union, ∪, and intersection, ∩, are the usual lattice operations. The mapping ϕ is called a "valuation" and A is a 'Valuation lattice." If R is a lattice-valued ring and a mapping d is defined by

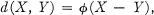
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 159 - 165
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Albert, A. A., Structure of algebras, American Mathematical Society Colloquium Publications, Vol. 24 (New York, 1939).Google Scholar
2. Blumenthal, L. M., Boolean geometry I, Rend. Circ. Mat. Palermo, (2), 1 (1952), 343–360.Google Scholar
3. Ellis, David, Autometrized Boolean algebras I, Can. J. Math., 8 (1951), 87–93.Google Scholar
4. Ellis, David, -Geometry in abstract distance spaces, Publ. Math. Debrecen, 2 (1951), 1–25.Google Scholar
5. Jacobson, Nathan, Lectures in abstract algebras II (New York, 1953).Google Scholar
6. MacDuffee, Cyrus, Introduction to abstract algebra (London, 1940).Google Scholar
7. Menger, Karl, Beitrdge zur Gruppentheorie I, Math. Z., 83 (1931), 396–418.Google Scholar
8. Taussky, Olga, Zur Metrik der Gruppen, Anz. Akad. Wiss. Wien (1930), 140–142.Google Scholar
9. Zemmer, J. L., A Boolean geometry for the integers, Amer. Math. Monthly, 67 (1960), 56–57.Google Scholar