Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-01T21:39:22.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Multidimensional Vinogradov-type Estimates in Function Fields

Published online by Cambridge University Press:  20 November 2018

Wentang Kuo ,
Yu-Ru Liu  and
Xiaomei Zhao
Wentang Kuo
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics, University of Waterloo, Waterloo, ON N2L 3G1. e-mail: wtkuo@math.uwaterloo.ca, yrliu@math.uwaterloo.ca
Yu-Ru Liu
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics, University of Waterloo, Waterloo, ON N2L 3G1. e-mail: wtkuo@math.uwaterloo.ca, yrliu@math.uwaterloo.ca
Xiaomei Zhao
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan, Hubei, China 430079. e-mail: x8zhao@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 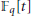${{\mathbb{F}}_{q}}\left[ t \right]$ denote the polynomial ring over the finite field 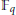${{\mathbb{F}}_{q}}$. We employ Wooley's new efficient congruencing method to prove certain multidimensional Vinogradov-type estimates in 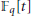${{\mathbb{F}}_{q}}\left[ t \right]$. These results allow us to apply a variant of the circle method to obtain asymptotic formulas for a system connected to the problem about linear spaces lying on hypersurfaces defined over 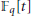${{\mathbb{F}}_{q}}\left[ t \right]$.

Keywords

16T3018D3520B3018D1020F55
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 844 - 873
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The research of the first two authors are supported by NSERC discovery grants, and the research of the third author is supported by NSFC (11126191) and NSFC(11201163). This work was completed when the third author visited the University of Waterloo in 2012, and she would like to thank the Department of Pure Mathematics for its hospitality.

References

[1] Birch, B. J., Homogeneous forms of odd degree in a large number of variables. Mathematika 4(1957), 102–105. http://dx.doi.org/10.1112/S0025579300001145 CrossRefGoogle Scholar
[2] Brauer, R., A note on systems of homogeneous algebraic equations. Bull. Amer. Math. Soc. 51(1945), 749–755. http://dx.doi.org/10.1090/S0002-9904-1945-08440-7 CrossRefGoogle Scholar
[3] Davenport, H. and Lewis, D. J., Homogeneous additive equations. Proc. Roy. Soc. Ser. A. 274(1963), 443–460. http://dx.doi.org/10.1098/rspa.1963.0143 Google Scholar
[4] Kubota, R. M., Waring's problem for Fq[x]. Ph. D. Thesis, University of Michigan, Ann Arbor, 1971.Google Scholar
[5] Lang, S., On quasi-algebraic closure. Ann. of Math. 55(1952), 373–390. http://dx.doi.org/10.2307/1969785 CrossRefGoogle Scholar
[6] Liu, Y.-R. and Wooley, T. D., Waring's problem in function fields. J. Reine Angew. Math. 638(2010), 1–67. http://dx.doi.org/10.1515/crelle.2010.001 CrossRefGoogle Scholar
[7] Parsell, S. T., A generalization of Vinogradov's mean value theorem. Proc. London Math. Soc. (3) 91(2005), no. 1, 1–32. http://dx.doi.org/10.1112/S002461150501525X CrossRefGoogle Scholar
[8] Parsell, S. T.,Asymptotic estimates for rational linear spaces on hypersurfaces. Trans. Amer. Math. Soc. 361(2009), no. 6, 2929–2957. http://dx.doi.org/10.1090/S0002-9947-09-04821-1 CrossRefGoogle Scholar
[9] Parsell, S. T., Prendivlle, S. M., and Wooley, T. D., Near-optimal mean value estimates for multidimensional Weyl sums. http://arxiv:1205.6331 Google Scholar
[10] Wooley, T. D., Large improvements in Waring's problem. Ann. of Math. 135(1992), no. 1, 131–164. http://dx.doi.org/10.2307/2946566 Google Scholar
[11] Wooley, T. D., A note on simultaneous congruences. J. Number Theory 58(1996), no. 2, 288–297. http://dx.doi.org/10.1006/jnth.1996.0078 CrossRefGoogle Scholar
[12] Wooley, T. D., Vinogradov's mean value theorem via efficient congruencing. Ann. of Math. 175(2012), no. 3, 1575–1627. http://dx.doi.org/10.4007/annals.2012.175.3.12 CrossRefGoogle Scholar
[13] Wooley, T. D., Vinogradov's mean value theorem via efficient congruencing. II. Duke Math. J. 162(2013), no. 4, 673–730. http://dx.doi.org/10.1215/00127094-2079905 CrossRefGoogle Scholar
[14] Wooley, T. D., The asymptotic formula in Waring's problem. Int. Math. Res. Not. IMRN 2012, no. 7, 1485–1504.Google Scholar
[15] Zhao, X., A note on multiple exponential sums in function fields. Finite Fields Appl. 18(2012), no. 1, 35–55. http://dx.doi.org/10.1016/j.ffa.2011.06.003 CrossRefGoogle Scholar
[16] Zhao, X., Asymptotic estimates for rational spaces on hypersurfaces in function fields. Proc. Lond. Math. Soc.(3) 104(2012), no. 2, 287–322. http://dx.doi.org/10.1112/plms/pdr031 CrossRefGoogle Scholar