Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-01T18:57:23.802Z Has data issue: false hasContentIssue false
  • English
  • Français

The Multiple Q-Construction

Published online by Cambridge University Press:  20 November 2018

J. F. Jardine
J. F. Jardine*
Affiliation:
University of Western Ontario, London, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Products, and closely associated questions of infinite loop space structure, have always been a source of trouble in higher algebraic K-theory. From the first description of the product in terms of the plus construction, up to the current tendency to let the infinite loop space machines do it, the constructions have never been completely explicit, and many mistakes have resulted.

Since Waldhausen introduced the double Q-construction [16], there has been the tantalizing prospect of an infinite loop space structure for the nerve 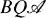of the Q-construction 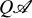of an exact category 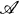, which would be understandable to the man on the street, and which also would be well-behaved with respect to products induced by biexact pairings. Gillet [3] showed that most of these conditions could be met with his introduction of the multiple Q-construction 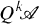. Shimakawa [14] filled in some of the details later.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 5 , 01 October 1987 , pp. 1174 - 1209
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Bousfield, A. K. and Friedlander, E. M., Homotopy theory of Γ-spaces, spectra and bisimplicial sets, Springer Lecture Notes in Math. 658 (1978), 80–150.Google Scholar
2. Gabriel, P. and Zisman, M., Calculus of fractions and homotopy theory, (Springer-Verlag, New York, 1967).CrossRefGoogle Scholar
3. Gillet, H., Riemann-Roch theorems for higher algebraic K-theory\, Advances in Math. 40 (1981), 203–289.Google Scholar
4. Grayson, D., Higher algebraic K-theory II, Springer Lecture Notes in Math. 551 (1976), 217–240.CrossRefGoogle Scholar
5. Grayson, D., Products in K-theory and intersecting algebraic cycles, Inv. Math. 47 (1978), 71–83.Google Scholar
6. Jardine, J. F., Simplicial presheaves, to appear in J. Pure Applied Algebra.Google Scholar
7. Jardine, J. F., Stable homotopy theory of simplicial presheaves, to appear in Can. J. Math.Google Scholar
8. Loday, J.-L., K-théorie algébrique et représentations de groupes, Ann. scient. Éc. Norm. Sup., 4e série, t. 9 (1976), 309–377.Google Scholar
9. May, J. P., Pairings of categories and spectra, J. Pure Applied Algebra 19 (1980), 299–346.Google Scholar
10. Quillen, D., Homotopical algebra, Springer Lecture Notes in Math. 43 (1967).CrossRefGoogle Scholar
11. Quillen, D., Higher algebraic K-theory I, Springer Lecture Notes in Math. 341 (1973), 85–147.CrossRefGoogle Scholar
12. Segal, G., Categories and cohomology theories, Topology 13 (1974), 293–312.Google Scholar
13. Grothendieck, A. et al., Revêtements étales et groupe fondamental (SGA 1), Springer Lecture Notes in Math. 224 (1971).Google Scholar
14. Shimakawa, K., Multiple categories and algebraic K-theory, to appear in J. Pure Applied Algebra.Google Scholar
15. Thomason, R., Algebraic K-theory and étale cohomology, Ann. Scient. Éc. Norm. Sup., 4e série 18 (1985), 437–552.Google Scholar
16. Waldhausen, F., Algebraic K-theory of generalized free products, Part I, Ann. Math. 108 (1978), 135–204.Google Scholar