Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-01T19:43:43.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplication Operators

Published online by Cambridge University Press:  20 November 2018

Martin Schechter
Martin Schechter*
Affiliation:
University of California, Irvine, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let V(x) ≧ 0 be given on Rn and define

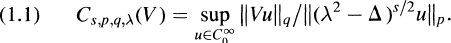
This constant has played a role in many investigation. For n — 3 it was shown in Courant-Hilbert [7] p. 446 that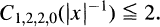 In [10], Kato estimates C2,2,2,ƛ(V) in terms of the L2 +L∞ norm of V in R3. Stummel [22] showed that C2,2,2,1(V) is bounded by 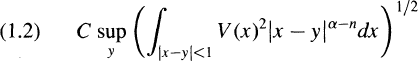in Rn, n > 2, provided α < 4. Browder [6] and Balslev [3] showed that Cs,q,q,ƛ(V) is bounded by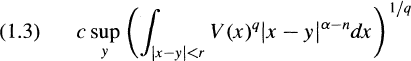

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 2 , 01 April 1989 , pp. 234 - 249
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Adams, D.R., On the existence of capacitary strong type estimates in Rn , Ark. Mat. 14 (1976), 125–140.Google Scholar
2. Aronszajn, N. and Smith, K.T., Theory of Bessel potentials, Ann. Inst. Fourier, Grenable 11 (1961), 385–475.Google Scholar
3. Balslev, E., The essential spectrum of elliptic differential operators in LP(Rn), Trans. Amer. Math. Soc. 116 (1965), 193–217.Google Scholar
4. Berger, M.S. and Schechter, M., Embedding theorems and quasi-linear elliptic boundary value problems for unbounded domains, Trans. Amer. Math. Soc. 172 (1972), 261–278.Google Scholar
5. Bergh, J. and Lofstrom, J., Interpolation spaces, (Springer-Verlag, 1976).Google Scholar
6. Browder, F.E., On the spectral theory of elliptic differential operators, Math. Ann. 142 (1961), 22–130.Google Scholar
7. Courant, R. and Hilbert, D., Methods of mathematical physics, I (Interscience, 1953).Google Scholar
8. Fefferman, C.L., The uncertainty principle, Bull. Amer. Math. Soc. 9 (1983), 129–206.Google Scholar
9. Fournier, J. and Stewart, J., Amalgams of Lp and Ip , Bull. Amer. Math. Soc. 13 (1985), 1–21.Google Scholar
10. Kato, T., Fundamental properties of Hamiltonian operators of Schrodinger type, Trans. Amer. Math. Soc. 70(1951), 195–211.Google Scholar
11. Kerman, R. and Sawyer, E., The trace inequality and eigenvalue estimates for Schrodinger operators, to appear.Google Scholar
12. Mazja, V.G., On the negative spectrum of multidimensional Schrodinger operator, Dokl. Akad. Dauk SSSR 144 (1962), 721–722.Google Scholar
13. Muckenhoupt, B. and Wheeden, R.L., Weighted norm inequalities for fractional inequalities, Trans. Amer. Math. Soc. 192 (1974), 251–275.Google Scholar
14. Schechter, M., Imbedding estimates involving new norms and applications, Bull. Amer. Math. Soc. 11 (1984) 163–166.Google Scholar
15. Schechter, M., Self adjoint operators, spectral and scattering theory, variational techniques, non-linear partial differential equations and related topics, Differential Equations, (North Holland Mathematics Studies 92, Amsterdam, 1984), 501–509.Google Scholar
16. Schechter, M., Spectra of partial differential operators (North Holland,Amsterdam, 1986).Google Scholar
17. Schechter, M., Hamiltonians for singular potentials, Indiana Univ. Math. J. 22 (1972), 483–503.Google Scholar
18. Schechter, M., On the essential spectrum of an elliptic operator perturbed by a potential, J. d'Analyse Math. 22 (1969), 87–115.Google Scholar
19. Schechter, M., On the invariance of the essential spectrum of an arbitrary operator 11, Ricerche di Mat. 16 (1967), 3–26.Google Scholar
20. Schechter, M., The spectrum of the Schrodinger operators, to appear.Google Scholar
21. Simon, B. Quantum mechanics for Hamiltonians defined as quadratic forms (Princeton Univ. Press, 1971).Google Scholar
22. Stummel, F., Singular e elliptische Differential operatoren in Hilbertschen Raumen, Math. Ann. 132 (1956), 150–176.Google Scholar