Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T21:54:04.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent Orbit Varieties and the Atomic Decomposition of the Q-Kostka Polynomials

Published online by Cambridge University Press:  20 November 2018

William Brockman  and
Mark Haiman
William Brockman
Affiliation:
Dept. of Mathematics, Wells Hall Michigan State Univ. East Lansing, MI 48824 USA, e-mail: brockman@math.msu.edu
Mark Haiman
Affiliation:
Dept. of Mathematics Univ. California San Diego La Jolla, CA, 92093-0112 USA, e-mail: mhaiman@macaulay.ucsd.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the coordinate rings of 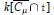$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$ scheme-theoretic intersections of nilpotent orbit closures with the diagonal matrices. Here 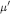${\mu }'$ gives the Jordan block structure of the nilpotent matrix. de Concini and Procesi [5] proved a conjecture of Kraft [12] that these rings are isomorphic to the cohomology rings of the varieties constructed by Springer [22, 23]. The famous $q$-Kostka polynomial 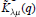${{\tilde{K}}_{\lambda \mu }}(q)$ is the Hilbert series for the multiplicity of the irreducible symmetric group representation indexed by 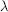$\lambda $ in the ring 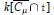$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$. Lascoux and Schützenberger [15, 13] gave combinatorially a decomposition of 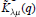${{\tilde{K}}_{\lambda \mu }}(q)$ as a sum of “atomic” polynomials with non-negative integer coefficients, and Lascoux proposed a corresponding decomposition in the cohomology model.

Our work provides a geometric interpretation of the atomic decomposition. The Frobenius-splitting results of Mehta and van der Kallen [19] imply a direct-sum decomposition of the ideals of nilpotent orbit closures, arising from the inclusions of the corresponding sets. We carry out the restriction to the diagonal using a recent theorem of Broer [3]. This gives a direct-sum decomposition of the ideals yielding the 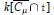$k\left[ \overline{{{\text{C}}_{\mu }}}\,\bigcap \,\text{t} \right]$, and a new proof of the atomic decomposition of the $q$-Kostka polynomials.

Keywords

05E1014M9920G0505E15q-Kostka polynomialsatomic decompositionnilpotent conjugacy classesnilpotent orbit varieties
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 525 - 537
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Bayer, D. and Stillman, M., Macaulay 2: A systemfor computation in algebraic geometry and commutative algebra. Computer software, 1996–7. http://www.math.uiuc.edu/Macaulay2/. Google Scholar
2. Bergeron, N. and Garsia, A., On certain spaces of harmonic polynomials. Contemporary Math. (86) 138, 1992.Google Scholar
3. Broer, A., The sum of generalized exponents and Chevalley's restriction theorem for modules of covariants. Indag. Math. (N.S.) (4) 6(1995), 385–396.Google Scholar
4. Carrell, J.B., Orbits of the Weyl group and a theorem of de Concini and Procesi. Compositio Math. (1) 60(1986), 45–52.Google Scholar
5. de Concini, C. and Procesi, C., Symmetric functions, conjugacy classes, and the flag variety. Invent.Math. 64(1981), 203–219.Google Scholar
6. Foulkes, H.O., A survey of some combinatorial aspects of symmetric functions. In: Permutations (Actes Colloq. Université René Descartes, Paris, 10-13 juillet 1972), 79–92. Gauthier-Villars, Paris, 1974.Google Scholar
7. Garsia, A. and Procesi, C., On certain graded Sn-modules and the q-Kostka polynomials. Adv. Math. 94(1992), 82–138.Google Scholar
8. Gutkin, E.A., Representations of the Weyl group in the space of vectors of zero weight. Uspehi. Mat. Nauk 28(1973), 237–238.Google Scholar
9. Hotta, R. and Springer, T.A., A specialization theorem for certain Weyl group representations and an application to the Green polynomials of unitary groups. Invent. Math. 41(1977), 113–127.Google Scholar
10. Kostant, B., Lie group representations on polynomial rings. Amer. J.Math. 86(1963), 327–404.Google Scholar
11. Kostant, B., On Macdonald's η-function formula, the Laplacian and generalized exponents. Adv. Math. 20(1976), 179–212.Google Scholar
12. Kraft, H., Conjugacy classes and Weyl group representations. Astérisque 87–88(1981), 191–205.Google Scholar
13. Lascoux, A., Cyclic permutations on words, tableaux, and harmonic polynomials. In: Proceedings of the Hyderabad Conference on Algebraic Groups (Hyderabad, 1989). Manoj Prakashan, Madras, 1991. 323–347.Google Scholar
14. Lascoux, A. and Schützenberger, M. P., Croissance des polynômes Foulkes-Green. C. R. Acad. Sci. Paris Sér. A 288(1979), 95–98.Google Scholar
15. Lascoux, A. and Schützenberger, M. P., Le monoïde plaxique. In: Noncommutative structures in Algebra and Geometric Combinatorics 109. CNR, Rome, 1981, 129–156.Google Scholar
16. Lusztig, G., Green polynomials and singularities of unipotent classes. Adv. inMath. 42(1981), 169–178.Google Scholar
17. Lusztig, G., Singularities, character formulas, and a q-analog of weight multiplicities. Analyse et topologie sur les espaces singuliers (II-III), Astérisque 101–102(1983), 208–227.Google Scholar
18. Macdonald, I.G., Symmetric Functions and Hall Polynomials. Oxford Mathematical Monographs. Second edition, Oxford University Press, 1995.Google Scholar
19. Mehta, V.B. and van der Kallen, W., A simultaneous Frobenius splitting for closures of conjugacy classes of nilpotent matrices. Compositio Math. (2) 84(1992), 211–221.Google Scholar
20. Schützenberger, M., Propriétés nouvelles des tableaux de Young. In: Théorie des nombres: Séminaire Delange-Pisot-Poitou, 19e année, volume 2, Paris, 1978. SecrétariatMath. (Exp. 26, 14 pages).Google Scholar
21. Spaltenstein, N., On the fixed point set of a unipotent transformation on the flag manifold. Proc. Kon. Nederl. Akad. Wetensch. 79(1976), 452–456.Google Scholar
22. Springer, T.A., Trigonometric sums, Green functions of finite groups and representations of Weyl groups. Invent. Math. 36(1976), 173–207.Google Scholar
23. Springer, T.A. , A construction of representations of Weyl groups. Invent. Math. 44(1978), 279–293.Google Scholar
24. Steinberg, R., On the desingularization of the unipotent variety. Invent. Math. 36(1976), 209–224.Google Scholar
25. Tanisaki, T., Defining ideals of the closures of the conjugacy classes and representations of the Weyl groups. Tôhoku Math. J. 34(1982), 575–585.Google Scholar
26. Weyman, J., The equations of conjugacy classes of nilpotent matrices. Invent. Math. (2) 98(1989), 229–245.Google Scholar