Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-08T20:14:28.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonzero Symmetry Classes of Smallest Dimension

Published online by Cambridge University Press:  20 November 2018

G. H. Chan  and
M. H. Lim
G. H. Chan
Affiliation:
Nanyang University, Singapore
M. H. Lim
Affiliation:
University of Malaya, Kuala Lumpur, Malaysia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let U be a k-dimensional vector space over the complex numbers. Let ⊗m U denote the mth tensor power of U where m ≧ 2. For each permutation σ in the symmetric group Sm, there exists a linear mapping P(σ) on ⊗mU such that

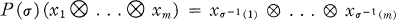
for all x1, …, xm in U.

Let G be a subgroup of Sm and λ an irreducible (complex) character on G. The symmetrizer

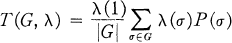
is a projection of ⊗ mU. Its range is denoted by Uλm(G) or simply Uλ(G) and is called the symmetry class of tensors corresponding to G and λ.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 4 , April 1980 , pp. 957 - 968
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Boerner, H., Representations of groups (North Holland/American Elsevier, Amsterdam-London/New York, 1970).Google Scholar
2. Brauer, R., Investigations on group characters, Ann. of Math. 42 (1941), 926–985.Google Scholar
3. Burnside, W., Theory of groups of finite order (Reprinted by Dover, New York, 1955).Google Scholar
4. Chan, G. H., On a class of permutation groups, Nanta Math. 6 (1973), 100–105.Google Scholar
5. Chan, G. H., Construction of minimal (k)-groups, Nanta Math. 7 (1974), 30–35.Google Scholar
6. Chan, G. H., A characterization of minimal (k)-groups of degree n ≧ 3k, Linear and Multilinear Algebra 4 (1977), 285–305.Google Scholar
7. Chan, G. H., On the triviality of symmetry class of tensors, Linear and Multilinear Algebra 6 (1978), 73–82.Google Scholar
8. Chan, G. H., (k)-character and the triviality of symmetry classes, Linear Algebra Appl. (to appear).CrossRefGoogle Scholar
9. Chan, G. H., A note on symmetrizers of rank one, Nanta Math. 11 (1979), 130–133.Google Scholar
10. Chang, S. C., On the vanishing of a (G,a) space, Chinese J. Math. 4 (1976), 1–7.Google Scholar
11. Curtis, U. C. and Reiner, I., Representation theory of finite groups and associative algebras (Interscience, New York-London, 1962).Google Scholar
12. Dieudonné, J. and Carrell, J. B., Invariant theory, old and new (Academic Press, New York, 1971).Google Scholar
13. Freese, R., Inequalities for generalized matrix functions based on arbitrary characters, Linear Algebra Appl. 7 (1973), 337–345.Google Scholar
14. Grone, R., A note on the dimension of an orbital subspace, Linear Algebra Appl. 17 (1977), 283–286.Google Scholar
15. Kerber, A., Representations of permutation groups I, Lecture Notes in Mathematics 240 (Springer-Verlag, New York, 1971).CrossRefGoogle Scholar
15. Lim, M. H., Regular symmetry classes of tensors, Nanta Math. 8 (1975), 42–46.Google Scholar
17. Marcus, M., Finite dimensional multilinear algebra, Part 1 (Marcel Dekker, New-York, 1973).Google Scholar
18. Marcus, M., Finite dimensional multilinear algebra, Part II (Marcel Dekker, New York, 1975).Google Scholar
19. Merris, R., The dimensions of certain symmetry classes of tensors II, Linear and Multilinear Algebra 4 (1976), 205–207.'Google Scholar
20. Merris, R., Relations among generalized matrix functions, Pacific J. Math. 62 (1970), 153–161.Google Scholar
21. Merris, R., Nonzero decomposable symmetrized tensors, Linear Algebra Appl. 17 (1977), 287–292.Google Scholar
22. Merris, R., On vanishing decomposable symmetrized tensors, Linear and Multilinear Algebra 5 (1977), 79–86.Google Scholar
23. Merris, R., Recent advances in symmetry classes of tensors, preprint.CrossRefGoogle Scholar
24. Merris, R. and Pierce, S., Elementary divisors of higher degree associated transformations, Linear and Multilinear Algebra 1 (1973), 241–250.Google Scholar
25. Merris, R. and Rashid, M. A., The dimensions of certain symmetry classes of tensors, Linear and Multilinear Algebra 2 (1974), 245–248.Google Scholar
26. Singh, K., On the vanishing of a pure product in a (G,a) space, Ph.D. Thesis, University of British Columbia (1967).Google Scholar
27. Westwick, R., A note on symmetry classes of tensors, J. Algebra, 15 (1970), 309–311.Google Scholar
28. Williamson, S. G., Symmetry operators of Kranz products, J. Comb. Theory 11 (1971), 122–138.Google Scholar