Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-01T06:04:09.189Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Young's Raising Operator

Published online by Cambridge University Press:  20 November 2018

Glânffrwd P. Thomas
Glânffrwd P. Thomas*
Affiliation:
Open University Production Centre, Milton Keynes, Great Britain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the following formula due to Young [7] for the calculation of the homogeneous product sum, hλ, in terms of Schur functions;

where the operation Srs is defined as follows:

Y1: Srs, where r < s, “represents the operation of moving one letter from the s-th row up to the r-th row; and the resulting term is regarded as zero, when any row becomes less than a row below it, or when letters from the same row overlap; as, for instance, happens when λ1 = λ2 in the case of S13S23.“

The following example of the above is given by Robinson [4].

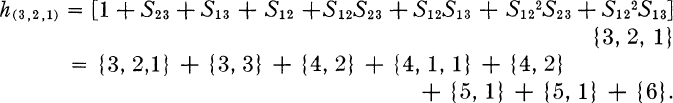
Calculation by other means shows that the above analysis of h(3,2,1) is correct; however, it will be noticed that the operator S123S23 does not appear in the above yet it is not specifically excluded by the rule Y1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 49 - 54
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Hall, P., The algebra of partitions, From the proceedings of the Fourth Canadian Math. Congress, Banff (1957), 147–159.Google Scholar
2. Littlewood, D. E., On certain symmetric functions, Proc. London Math. Soc. 11 (1961), 485–498.Google Scholar
3. Read, R. C., The use of S-functions in combinatorial analysis, Can. J. Math. 20 (1968), 808–841.Google Scholar
4. de, G., Robinson, B., On the representations of the symmetric group, Amer. J. Math. 60 (1938), 745–760.Google Scholar
5. Thomas, G. P., Schur functions and Baxter algebras, Ph.D. Thesis, University College of Swansea, Wales (1974).Google Scholar
6. Thomas, G. P., Further results on Baxter sequences and generalized Schur functions, in Combinatoire et représentation du groupe symétrique, Lecture Notes in Mathematics 579 (Springer-Verlag, Berlin/Heidelberg/New York), 155–167.Google Scholar
7. Young, A., Quantitive substitutional analysis, Part VI, Proc. London Math. Soc. 34 (1932), 196–230.Google Scholar