Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-08T20:50:13.937Z Has data issue: false hasContentIssue false
  • English
  • Français

Note Upon The Generalized Cayleyan Operator

Published online by Cambridge University Press:  20 November 2018

H. W. Turnbull
H. W. Turnbull*
Affiliation:
The University, St. Andrews, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following note which deals with the effect of a certain determinantal operator when it acts upon a product of determinants was suggested by the original proof which Dr. Alfred Young gave of the property

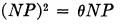
subsisting between the positive P and the negative N substitutional operators, θ being a positive integer. This result which establishes the idempotency of the expression θ−1NP within an appropriate algebra is fundamental in the Quantitative Substitutional Analysis that Young developed.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 1 , Issue 1 , 01 February 1949 , pp. 48 - 56
Copyright
Copyright © Canadian Mathematical Society 1949

References

[1] Capelli, A., Math. Ami., vol. 29 (1887), 331–338.Google Scholar
[2] Cayley, A., Collected Works, vol. 1 (1845), 80-94, 95–112.Google Scholar
[3] Grace, J. H. and Young, A., The Algebra of Invariants (Cambridge, 1903), 259.Google Scholar
[4] Turnbull, H. W., Theory of Determinants, Matrices and Invariants (Glasgow, 1928; 2nd ed. 1945).Google Scholar
[5] Young, A., “Quantitative Substitutional Analysis,” Troc. London Math. Soc. (1) vol. 34 (1902), 361–397, in particular p. 364.Google Scholar