No CrossRef data available.
Article contents
On a Certain Residual Spectrum of Sp8
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let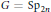 
$G=\text{S}{{\text{p}}_{\text{2n}}}$ be the symplectic group defined over a number field 
$F$. Let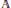 
$\mathbb{A}$ be the ring of adeles. A fundamental problem in the theory of automorphic forms is to decompose the right regular representation of 
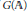$G\left( \mathbb{A} \right)$ acting on the Hilbert space 
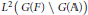${{L}^{2}}\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)$. Main contributions have been made by Langlands. He described, using his theory of Eisenstein series, an orthogonal decomposition of this space of the form:
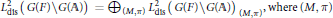$L_{dis}^{2}\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)\,=\,{{\oplus }_{\left( M,\,\pi \right)}}L_{dis}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\,\pi \right)}},\,\text{where}\,\left( M,\,\pi \right)$ is a Levi subgroup with a cuspidal automorphic representation 
$\pi $ taken modulo conjugacy. (Here we normalize $\pi $ so that the action of the maximal split torus in the center of 
$G$ at the archimedean places is trivial.) and
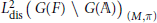$L_{\text{dis}}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\pi \right)}}$ is a space of residues of Eisenstein series associated to 
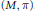$\left( M,\,\pi \right)$. In this paper, we will completely determine the space
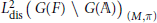$L_{\text{dis}}^{2}{{\left( G\left( F \right)\backslash G\left( \mathbb{A} \right) \right)}_{\left( M,\pi \right)}}$, when 
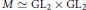$M\simeq \text{G}{{\text{L}}_{2}}\times \text{G}{{\text{L}}_{2}}$. This is the first result on the residual spectrum for non-maximal, non-Borel parabolic subgroups, other than 
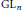$\text{G}{{\text{L}}_{n}}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
[1] Arthur, J., Eisenstein series and the trace formula. In: Proc. Sympos. in Pure Mathematics, Part I
33, Amer. Math. Soc., Providence, RI, 1979, 253–274.Google Scholar
[2] Arthur, J., On some problems suggested by the trace formula. In: Lie group representations II, Lecture Notes in Math. 1041, Springer-Verlag, 1984, 1–49.Google Scholar
[3] Borel, A., Automorphic L-functions, Automorphic Forms and Automorphic Representations. In: Proc. Sympos. Pure Mathematics, Part II 33, Amer. Math. Soc., Providence, RI, 1979, 27–61.Google Scholar
[4] Borel, A. and Wallach, N., Continuous cohomolgy, discrete subgroups, and representations of reductive groups. In: Ann. of Math. Stud.
94
Princeton University Press, Princeton, 1980.Google Scholar
[5] Casselmam, W. and Shahidi, F., On irreducibility of standard modules for generic representations. Ann. Sci. École Norm. Sup.
31(1998), 561–589.Google Scholar
[6] Gelbart, S., Automorphic forms on Adele groups. In: Ann. of Math. Stud.
83, Princeton University Press, Princeton, 1975.Google Scholar
[7] Gelbart, S. and Jacquet, H., A relation between automorphic representations of GL(2) and GL(3)
. Ann. Sci. École Norm. Sup.
11(1978), 471–552.Google Scholar
[8] Gelbart, S. and Shahidi, F., Analytic Properties of Automorphic L-functions. In: Perspect. Math.
6, Academic Press, New York, 1988.Google Scholar
[9] Goldberg, D., Reducibility of induced representations for Sp(2n) and SO(n)
. Amer. J. Math.
116(1994), 1101–1151.Google Scholar
[10] Jacquet, H., On the residual spectrum of GL(n)
. In: Lie Group Representations II, Lecture Notes in Math. 1041, Springer-Verlag, 1983, 185–208.Google Scholar
[11] Jacquet, H. and Langlands, R. P., Automorphic Forms on GL(2). Lecture Notes in Math. 114, Springer-Verlag, 1970.Google Scholar
[12] Jantzen, C. and Kim, H., Parameterization of the image of normalized intertwining operators. Pacific J. Math., to appear.Google Scholar
[13] Keys, C. D., On the decomposition of reducible principal series representations of p-adic Chevalley groups. Pacific J. Math.
101(1982), 351–388.Google Scholar
[14] Keys, C. D. and Shahidi, F., Artin L-functions and normalization of intertwining operators. Ann. Sci. École Norm. Sup.
21(1988), 67–89.Google Scholar
[16] Kim, H., Residual spectrum of odd-orthogonal groups. Int. Math. Res. Not.
17(2001), 873–906.Google Scholar
[18] Kim, H., The residual spectrum of split classical groups: contribution from Borel subgroups. Pacific J. Math., to appear.Google Scholar
[19] Kim, H. and Shahidi, F., Quadratic unipotent Arthur parameters and residual spectrum of Sp2
n
. Amer. J. Math. (2)
118(1996), 401–425.Google Scholar
[20] Kim, H. and Shahidi, F., Symmetric cube L-functions for GL2
are entire. Ann. of Math.
150(1999), 645–662.Google Scholar
[21] Konno, Takuya, The residual spectrum of U(2; 2)
, Trans. Amer. Math. Soc. (4)
350(1998), 1285–1358.Google Scholar
[22] Kudla, Stephen S., Rallis, Stephen and Soudry, David, On the degree 5 L-function for Sp2
. Invent. Math. (3)
107(1992), 483–541.Google Scholar
[23] Labesse, J. P. and Langlands, R. P., L-indistinguishability for SL(2)
. Canad. J. Math.
31(1979), 726–785.Google Scholar
[25] Langlands, R. P., On the Functional Equations Satisfied by Eisenstein Series. In: Lecture Notes in Math.
544, Springer-Verlag, 1976.Google Scholar
[26] Moeglin, C., Orbites unipotentes et spectre discret non ramiè, Le cas des groupes classiques déployś. Compositio Math.
77(1991), 1–54.Google Scholar
[27] Moeglin, C., Représentations unipotentes et formes automorphes de carré intégrable. Forum Math.
6(1994), 651–744.Google Scholar
[28] Moeglin, C. and Waldspurger, J. L., Décomposition spectrale et séries d'Eisenstein, paraphrase sur l'Ecriture. In: Progress in Math., Birkhäuser, 1994.Google Scholar
[29] Moeglin, C. and Waldspurger, J. L., Le spectre résiduel de GL(n)
. Ann. Sci. École Norm. Sup.
22(1989), 605–674.Google Scholar
[30] Shahidi, F., Automorphic L-functions: a survey. In: Automorphic forms, Shimura varieties, and L-functions
II, Ann Arbor, MI, 1988, 1990, Academic Press, 415–437.Google Scholar
[32] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measure; complementary series for p-adic groups. Ann. of Math.
132(1990), 273–330.Google Scholar
[33] Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions. Ann. of Math.
127(1988), 547–584.Google Scholar
[34] Zampera, S., The residual spectrum of the group of the type G2
. J. Math. Pures Appl. (9) 76(1997), 805–835.Google Scholar
You have
Access