Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-01T19:44:02.388Z Has data issue: false hasContentIssue false
  • English
  • Français

On Certain Polynomials of Gaussian Type

Published online by Cambridge University Press:  20 November 2018

Daniel Reich
Daniel Reich*
Affiliation:
Temple University, Philadelphia, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. We shall consider functions of the form

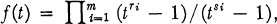
where {ri} and {si} are sets of positive integers. Such functions were studied by E. Grosswald in [2], who took {si} to be pairwise relatively prime, and asked the following two questions:

(a) When is ƒ(t) a polynomial?

(b) When does ƒ(t) have positive coefficients?

These questions arise naturally from the work of Allday and Halperin, who show in [1] that under suitable circumstance ƒ(t) will be the Poincare polynomial of the orbit space of a certain Lie group action. Grosswald gives a complete answer to (a), but (b) is a much harder question, and a complete answer is provided only for the case m = 2. His treatment involves the representation of the coefficients of ƒ(t) by partition functions, and uses a classical description by Sylvester of the semigroup generated by {si}.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 274 - 281
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Allday, C. and Halperin, S., Lie group actions on spaces of finite rank, Quart. J. of Math., Oxford, (to appear).Google Scholar
2. Grosswald, E., Reducible rational fractions of the type of Gaussian polynomials with only nonnegative coefficientsj Canadian Math. Bull., (to appear).Google Scholar
3. Nijenhuis, A. and Wilf, H., Representations of integers by linear forms in non-negative integers, J. of Number Theor. 4 (1972), 98–106.Google Scholar
4. Sylvester, J., A constructive theory of partitions, Amer. J. Math. 5 (1882), 251–330.Google Scholar
5. Sylvester, J., Mathematical questions with their solutions, Educational Times 41 (1884), p. 21.Google Scholar