No CrossRef data available.
Article contents
On Conics Over a Finite Field
Published online by Cambridge University Press: 20 November 2018
Extract
Let F denote a Galois field of order q and odd characteristic p, and F* = F\{0}. Let Sn denote an n-dimensional affine space with base field F. E. Cohen [1] had proved that if n ≧ 4, there is no hyperplane of Sn contained in the complement of the quadric Qn of Sn defined by
1.1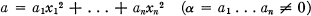
and in S3, there are q + 1 or 0 planes contained in the complement of Q3 according as — aα is not or is a square of F.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974




