Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-06-08T13:16:30.075Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Existence of Positive Decaying Entire Solutions for a Class of Sublinear Elliptic Equations

Published online by Cambridge University Press:  20 November 2018

Yasuhiro Furusho  and
Takaŝi Kusano
Yasuhiro Furusho
Affiliation:
Saga University, Saga, Japan
Takaŝi Kusano
Affiliation:
Hiroshima University, Hiroshima, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent years there has been a growing interest in the existence and asymptotic behavior of entire solutions for second order nonlinear elliptic equations. By an entire solution we mean a solution of the elliptic equation under consideration which is guaranteed to exist in the whole Euclidean N-space RN, N ≧ 2. For standard results on the subject the reader is referred to the papers [2-7, 9-21].

The study of entire solutions, which at an early stage was restricted to simple equations of the form Δu + f(x, u) = 0, x ∊ RN, Δ being the N-dimensional Laplacian, has now been extended and generalized to elliptic equations of the type

A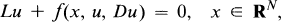

where

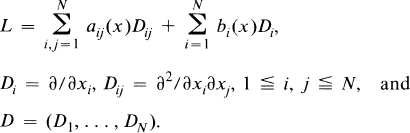
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1156 - 1173
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Akô, K. and Kusano, T., On bounded solutions of second order elliptic differential equations, J. Fac. Sci. Univ. Tokyo, Sect. I 11 (1964), 29–37.Google Scholar
2. Allegretto, W., On positive L°° solutions of a class of elliptic systems, Math. Z. 191 (1986), 479–484.Google Scholar
3. Allegretto, W. and Huang, Y. X., Positive solutions of semilinear elliptic equations with specified behaviour at ∞, (to appear).Google Scholar
4. Berestycki, H. and Lions, P. L., Nonlinear scalar field equations I; II, Arch. Rational Mech. Anal. 82 (1983), 313–345; 347–375.Google Scholar
5. Fukagai, N., Existence and uniqueness of entire solutions of second order sublinear elliptic equations, Funkcial. Ekvac. 29 (1986), 151–165.Google Scholar
6. Furusho, Y., Positive solutions of linear and quasilinear elliptic equations in unbounded domains, Hiroshima Math. J. 15 (1985), 173–220.Google Scholar
7. Furusho, Y., Existence of global positive solutions of quasilinear elliptic equations in unbounded domains, Funkcial. Ekvac, (to appear).Google Scholar
8. Furusho, Y. and Ogura, Y., On the solutions of linear elliptic equations in exterior domains, J. Differential Equations 50 (1983), 348–374.Google Scholar
9. Gidas, B., Ni, W.-M. and Nirenberg, L., Symmetry of positive solutions of nonlinear elliptic equations in RN , Advances in Math. Supplementary Studies 7A (1984), 369–402.Google Scholar
10. Kawano, N., On bounded entire solutions of semilinear elliptic equations, Hiroshima Math. J. 74 (1984), 125–158.Google Scholar
11. Kusano, T. and Naito, M., Positive entire solutions of superlinear elliptic equations, Hiroshima Math. J. 16 (1986), 361–366.Google Scholar
12. Kusano, T. and Oharu, S., On entire solutions of second order semilinear elliptic equations, J. Math. Anal. Appl. 113 (1986), 123–135.Google Scholar
13. Kusano, T. and Swanson, C. A., Decaying entire positive solutions of quasilinear elliptic equations, Monatsh. Math. 101 (1986), 39–51.Google Scholar
14. Kusano, T. and Usami, H., Positive solutions of a class of second order semilinear elliptic equations in the plane, Math. Ann. 268 (1984), 255–264.Google Scholar
15. Ni, W.-M., On the elliptic equation Δu + K(x)u(n + 2)/(n − 2) = 0, its generalizations, and applications in geometry, Indiana Univ. Math. J. 31 (1982), 493–529.Google Scholar
16. Noussair, E. S. and Swanson, C. A., Positive solutions of quasilinear elliptic equations in exterior domains, J. Math. Anal. Appl. 75 (1980), 121–133.Google Scholar
17. Noussair, E. S. and Swanson, C. A., Decaying entire solutions of quasilinear elliptic equations, Funkcial. Ekvac. (to appear).Google Scholar
18. Noussair, E. S. and Swanson, C. A., Positive decaying entire solutions of superlinear elliptic equations, Indiana Univ. Math. J. (to appear).Google Scholar
19. Swanson, C. A., Positive solutions of —Δw = f(x, u), Nonlinear Anal. 9 (1985), 1319–1323.Google Scholar
20. Usami, H., On bounded positive entire solutions of semilinear elliptic equations, Funkcial. Ekvac. 29 (1986), 189–195.Google Scholar
21. Walter, W., Entire solutions of the differential equation Δu = f(u), J. Austral. Math. Soc. 50 (1981), 366–368.Google Scholar