Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-05-04T07:04:10.326Z Has data issue: false hasContentIssue false
  • English
  • Français

On the pluriclosed flow on Oeljeklaus–Toma manifolds

Part of: Global differential geometry

Published online by Cambridge University Press:  27 December 2022

Elia Fusi  and
Luigi Vezzoni Open the ORCID record for Luigi Vezzoni [Opens in a new window]
Elia Fusi
Affiliation:
Dipartimento di Matematica G. Peano, Università di Torino, Via Carlo Alberto 10, 10123 Torino, Italy e-mail: elia.fusi@unito.it
Luigi Vezzoni*
Affiliation:
Dipartimento di Matematica G. Peano, Università di Torino, Via Carlo Alberto 10, 10123 Torino, Italy e-mail: elia.fusi@unito.it
*
e-mail: luigi.vezzoni@unito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the pluriclosed flow on Oeljeklaus–Toma manifolds. We parameterize left-invariant pluriclosed metrics on Oeljeklaus–Toma manifolds, and we classify the ones which lift to an algebraic soliton of the pluriclosed flow on the universal covering. We further show that the pluriclosed flow starting from a left-invariant pluriclosed metric has a long-time solution 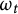$\omega _t$ which once normalized collapses to a torus in the Gromov–Hausdorff sense. Moreover, the lift of 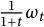$\tfrac {1}{1+t}\omega _t$ to the universal covering of the manifold converges in the Cheeger–Gromov sense to 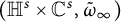$(\mathbb H^s\times \mathbb C^s, \tilde {\omega }_{\infty })$, where 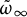$\tilde {\omega }_{\infty }$ is an algebraic soliton.

Keywords

Special Hermitian geometrypluriclosed flowOeljeklaus–Toma manifolds

MSC classification

Primary: 53C55: Hermitian and Kählerian manifolds
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 1 , February 2024 , pp. 39 - 65
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the GNSAGA of INdAM

References

Angella, D., Dubickas, A., Otiman, A., and Stelzig, J., On metric and cohomological properties of Oeljeklaus–Toma manifolds. Preprint, 2022. arXiv:2201.06377 Google Scholar
Angella, D. and Tosatti, V., Leafwise flat forms on Inoue–Bombieri surfaces. Preprint, 2021. arXiv:2106.16141 Google Scholar
Arroyo, R. M. and Lafuente, R. A., The long-time behavior of the homogeneous pluriclosed flow . Proc. Lond. Math. Soc. (3) 119(2019), no. 1, 266–289.CrossRefGoogle Scholar
Bismut, J.-M., A local index theorem for non-Kähler manifolds . Math. Ann. 284(1989), no. 4, 681–699.CrossRefGoogle Scholar
Boling, J., Homogeneous solutions of pluriclosed flow on closed complex surfaces . J. Geom. Anal. 26(2016), no. 3, 2130–2154.CrossRefGoogle Scholar
Enrietti, N., Fino, A., and Vezzoni, L., The pluriclosed flow on nilmanifolds and Tamed symplectic forms . J. Geom. Anal. 25(2015), no. 2, 883–909.CrossRefGoogle Scholar
Fang, S., Tosatti, V., Weinkove, B., and Zheng, T., Inoue surfaces and the Chern–Ricci flow . J. Funct. Anal. 271(2016), no. 11, 3162–3185.CrossRefGoogle Scholar
Fino, A., Kasuya, H., and Vezzoni, L., SKT and Tamed symplectic structures on solvmanifolds . Tohoku Math. J. (2) 67(2015), no. 1, 19–37.CrossRefGoogle Scholar
Garcia-Fernandez, M., Jordan, J., and Streets, J., Non-Kähler Calabi–Yau geometry and pluriclosed flow. Preprint. 2021. arXiv:2106.13716 Google Scholar
Gill, M., Convergence of the parabolic complex Monge–Ampère equation on compact Hermitian manifolds . Comm. Anal. Geom. 19(2011), 277–303.CrossRefGoogle Scholar
Inoue, M., On surfaces of Class  $VI{I}_0$ . Invent. Math. 24(1974), no.4, 269–320.CrossRefGoogle Scholar
Jordan, J. and Streets, J., On a Calabi-type estimate for pluriclosed flow . Adv. Math. 366(2020), Article no. 107097, 18 pp.CrossRefGoogle Scholar
Kasuya, H., Vaisman metrics on solvmanifolds and Oeljeklaus–Toma manifolds . Bull. Lond. Math. Soc. 45(2013), no. 1, 15–26.CrossRefGoogle Scholar
Lauret, J., Convergence of homogeneous manifolds . J. Lond. Math. Soc. (2) 86(2012), no. 3, 701–727.CrossRefGoogle Scholar
Lauret, J., Curvature flows for almost-Hermitian Lie groups . Trans. Amer. Math. Soc. 367(2015), no. 10, 7453–7480.CrossRefGoogle Scholar
Lauret, J. and Rodríguez Valencia, E. A., On the Chern–Ricci flow and its solitons for Lie group . Math. Nachr. 288(2015), no. 13, 1512–1526.CrossRefGoogle Scholar
Oeljeklaus, K. and Toma, M., Non-Kähler compact complex manifolds associated to number fields . Ann. Inst. Fourier (Grenoble) 55(2005), no. 1, 161–171.CrossRefGoogle Scholar
Otiman, A., Special Hermitian metrics on Oeljeklaus–Toma manifolds . Bull. Lond. Math. Soc. 54(2022), 655–667.CrossRefGoogle Scholar
Pujia, M. and Vezzoni, L., A remark on the Bismut–Ricci form on  $2$ -step nilmanifolds . C. R. Math. Acad. Sci. Paris 356(2018), no. 2, 222–226.CrossRefGoogle Scholar
Streets, J., Pluriclosed flow, Born–Infeld geometry, and rigidity results for generalized Kähler manifolds . Comm. Partial Differential Equations 41(2016), no. 2, 318–374.CrossRefGoogle Scholar
Streets, J., Pluriclosed flow on manifolds with globally generated bundles . Complex Manifolds 3(2016), 222–230.CrossRefGoogle Scholar
Streets, J., Pluriclosed flow on generalized Kähler manifolds with split tangent bundle . J. Reine Angew. Math. 739(2018), 241–276.CrossRefGoogle Scholar
Streets, J., Classification of solitons for pluriclosed flow on complex surfaces . Math. Ann. 375(2019), nos. 3–4, 1555–1595.CrossRefGoogle Scholar
Streets, J., Pluriclosed flow and the geometrization of complex surfaces . Prog. Math. 333(2020), 471–510.CrossRefGoogle Scholar
Streets, J. and Tian, G., A parabolic flow of pluriclosed metrics . Int. Math. Res. Not. IMRN 2010(2010), 3101–3133.Google Scholar
Streets, J. and Tian, G., Hermitian curvature flow . J. Eur. Math. Soc. (JEMS) 13(2011), no. 3, 601–634.Google Scholar
Streets, J. and Tian, G., Regularity results for pluriclosed flow . Geom. Topol. 17(2013), no. 4, 2389–2429.CrossRefGoogle Scholar
Tosatti, V. and Weinkove, B., The Chern–Ricci flow on complex surfaces . Compos. Math. 149(2013), no. 12, 2101–2138.CrossRefGoogle Scholar
Tosatti, V. and Weinkove, B., On the evolution of a Hermitian metric by its Chern–Ricci form . J. Differential Geom. 99(2015), no. 1, 125–163.CrossRefGoogle Scholar
Verbitsky, S., Surfaces on Oeljeklaus–Toma manifolds. Preprint, 2013. arXiv:1306.2456 Google Scholar
Vezzoni, L., A note on canonical Ricci forms on 2-step nilmanifolds . Proc. Amer. Math. Soc. 141(2013), no. 1, 325–333.CrossRefGoogle Scholar
Zheng, T., The Chern–Ricci flow on Oeljeklaus–Toma manifolds . Canad. J. Math. 69(2017), no. 1, 220–240.CrossRefGoogle Scholar