Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-28T06:02:48.935Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sieve of Eratosthenes

Published online by Cambridge University Press:  20 November 2018

M. Ram Murty  and
S. Saradha
M. Ram Murty
Affiliation:
McGill University, Montréal, Québec
S. Saradha
Affiliation:
Concordia University, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let v(n) denote the number of distinct prime factors of a natural number n. A classical theorem of Hardy and Ramanujan states that the normal order of v(n) is log log n. That is, given any , the number of natural numbers not exceeding x which fail to satisfy the inequality

1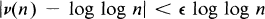

is o(x) as x → ∞. A very simple proof of this was subsequently given by Turán. He showed that

2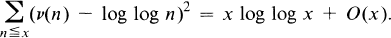

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 5 , 01 October 1987 , pp. 1107 - 1122
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Elliott, P. D. T. A., Probabilistic number theory I and II, (Springer Verlag, New York, 1980).CrossRefGoogle Scholar
2. Erdös, P., On the normal number oj prime factors of p — 1 and some related problems concerning the Euler's ϕ function, Quarterly Journal of Mathematics 6 (1935), 205–213.Google Scholar
3. Erdös, P. and Pomerance, C., On the normal number of prime factors of ϕ(n), Rocky Mountain Journal 75 (1985), 343–352.Google Scholar
4. Murty, M. Ram and Murty, V. Kumar, Prime divisors of Rourier coefficients of modular forms, Duke Math. Journal 51 (1984), 57–76.Google Scholar
5. Murty, M. Ram and Murty, V. Kumar, An analogue of the Erdös-Kac theorem for Rourier coefficients of modular forms, Indian Journal of Pure and App. Math. 15 (1984), 1090–1101.Google Scholar