Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-01T22:21:32.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive Finite Energy Solutions of Critical Semilinear Elliptic Problems

Published online by Cambridge University Press:  20 November 2018

Ezzat S. Noussair ,
Charles A. Swanson  and
Yang Jianfu
Ezzat S. Noussair
Affiliation:
School of Mathematics, University of New South Wales, Kensington, N.S.W., Australia 2033
Charles A. Swanson
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, British Columbia, V6T 1Y4
Yang Jianfu
Affiliation:
Department of Mathematics, Jiangxi University, Nanchang, Jiangxi 330047, People's Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

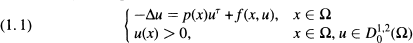Existence theorems and asymptotic properties will be obtained for boundary value problems of the form in an unbounded domain Ω⊆ RN(N ≥3) with smooth boundary, where Δ denotes the TV-dimensional Laplacian, τ — (N+ 2)/ (N — 2) is the critical Sobolev exponent, and 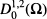is the completion of 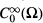in the L2(Ω) norm of .

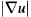Keywords

35J60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 5 , 01 October 1992 , pp. 1014 - 1029
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Ambrosetti, A. and Rabinowitz, P.H., Dual variational methods in critical point theory and applications, J. Funct. Anal. 14(1973), 349–381.Google Scholar
2. Benci, V. and Cerami, G., Existence of positive solutions of the equation — Δu+a(x)u = u(N+2)/(N-2), preprint.Google Scholar
3. Berestycki, H. and Lions, P.L., Nonlinear scalar field equations, I & II, Arch. Rational Mech. Anal. 82(1983), 313–375.Google Scholar
4. Brezis, H., Some variational problems with lack of compactness, Proc. Symp. in Pure Math. 45(1986), 165–201.Google Scholar
5. Brezis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Comm. Pure Appl. Math 36(1983), 437–477.Google Scholar
6. Brezis, H. and Lieb, E.H., A relation between pointwise convergence of functions and convergence of junctionals, Proc. Amer. Math. Soc. 88(1983), 486–490.Google Scholar
7. Ding, W.-Y. and W.-Ni, M., On the elliptic equation Δu+Ku(n+2)l(n-2) = 0 and related topics, Duke Math. J. 52(1985), 485–506.Google Scholar
8. Egnell, H., Semilinear elliptic equations involving critical Sobolev exponents, Arch. Rational Mech. Anal. 104(1988), 27–56.Google Scholar
9. Egnell, H., Elliptic boundary value problems with singular coefficients and critical nonlinearities, Indiana Univ. Math. J. 38(1989), 235–251.Google Scholar
10. Egnell, H., Existence results for some quasilinear elliptic equations, Proc. of the conference “Variational Problems”, Paris, June, 1988, to appear.Google Scholar
11. Egnell, H., Asymptotic results for finite energy solutions of semilinear elliptic equations, preprint.Google Scholar
12. Escobar, J.F., Positive solutions for some semilinear elliptic equations with critical Sobolev exponents, Comm. Pure Appl. Math. 40(1987), 623–657.Google Scholar
13. Gidas, B. and Spruck, J., Global and local behavior of positive solutions of nonlinear elliptic equations, Comm. Pure Appl. Math. 34(1981), 525–598.Google Scholar
14. Guedda, M. and Veron, L., Quasilinear elliptic equations involving critical Sobolev exponents, Nonlinear Anal. 13(1989), 879–902.Google Scholar
15. Li, Y. and W.-Ni, M., On conformai scalar curvature in RN, Duke. Math. J. 57(1988), 895–924.Google Scholar
16. Lieb, E.H., Sharp constants in the Hardy-Littlewood-Sobolev inequality and related inequalties, Ann. Of Math. (2)118(1983), 349–374.Google Scholar
17. Lions, P.L., The concentration-compactness principle in the Calculus of Variations. The locally compact case, Parts 1 & 2, Ann. Inst. H. Poincaré: Anal, non linéaire 1(1984), 109–145.& 223-283.Google Scholar
18. Lions, P.L., The concentration-compactness principle in the Calculus of Variations. The limit case, Parts 1 & 2, Revista Math. Iberoamericana(l) 1(1985), 145–201. (2) 1(1985), 46–120.Google Scholar
19. Ni, W.-M., On the elliptic equation δu + K(x)u(n+2)/(n-2) = 0, its generalizations, and applications to geometry, Indiana Univ. Math. J. 31(1982), 493–529.Google Scholar
20. Ni, W.-M. and Yotsutani, S., Semilinear elliptic equations of Matukuma-type and related topics, Japan J. Appl. Math. 5(1988), 1–32.Google Scholar
21. Noussair, E.S. and Swanson, C.A., Ground states for critical semilinear scalar field equations, Differential and Integral Equations, 5(1990), 875–887.Google Scholar
22. Talenti, G., Best constants in Sobolev inequality, Ann. Mat. Pura Appl. 110(1976), 353–372.Google Scholar
23. Taubes, C., The existence of a non-minimal solution to the SU(2) Yang-Mills-Higgs equations on R3, Comm. Math. Phys. 86(1982), 257–298.Google Scholar
24. Zhang, Dong, Positive solutions of nonlinear scalar field equations involving critical Sobolev exponent, Acta Math. Sinica N.S. 3(1987), 27–37.Google Scholar