Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-08T16:08:39.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of Harmonic Functions of Three Real Variables Given by Bergman-Whittaker Operators

Published online by Cambridge University Press:  20 November 2018

Josephine Mitchell
Josephine Mitchell*
Affiliation:
Pennsylvania State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 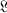be a closed rectifiable curve, not going through the origin, which bounds a domain Ω in the complex ζ-plane. Let X = (x, y, z) be a point in three-dimensional euclidean space E3 and set

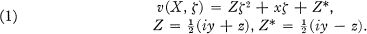
The Bergman-Whittaker operator defined by

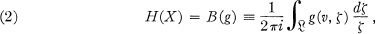
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 157 - 168
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Bergman, S., Zur Théorie der ein- und mehrwertigen harmonischen Funktionen des dreidimensionalen Raumes, Math. Z. 24 (1926), 641–669.Google Scholar
2. Bergman, S., On solutions with algebraic character of linear partial differential equations, Trans. Amer. Math. Soc. 68 (1950), 461–507.Google Scholar
3. Bergman, S., Integral operators in the theory of linear partial differential equations , Ergebnisse der Math. N. F. 23, Springer (1961).Google Scholar
4 Bergman, S., Some properties of a harmonic function of three variables given by its series development, Archive for Rational Mech. and Anal. (1961), 207-222.Google Scholar
5. Boas, R. P. Jr. , Entire functions, New York (1954).Google Scholar
6. Lindelôf, E., Le calcul des résidus et ses applications à la théorie des fonctions, London (1947).Google Scholar
7. Mitchell, J., Representation theorems for solutions of linear partial differential equations in three variables, Archive for Rational Mech. and Anal., 3 (1959), 439–459.Google Scholar
8. Titchmarsh, E. G., The theory of functions, 2nd éd., London (1939).Google Scholar