Hostname: page-component-84b7d79bbc-lrf7s Total loading time: 0 Render date: 2024-07-26T19:06:24.207Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on BMW Algebra, q-Schur Algebras and Categorification

Published online by Cambridge University Press:  20 November 2018

Pedro Vaz  and
Emmanuel Wagner
Pedro Vaz
Affiliation:
CAMGSD, Instituto Superior Técnico, Avenida Rovisco Pais, 1049-001 Lisboa, Portugal Institut de Recherche en Mathématique et Physique, Université Catholique de Louvain, Chemin du Cyclotron 2, 1348 Louvain-la-Neuve, Belgique. e-mail: pedro.vaz@uclouvain.be
Emmanuel Wagner
Affiliation:
Institut de Mathématiques de Bourgogne UMR 5584 du CNRS, 7 avenue Alain Savary BP 47870 21078 Dijon Cedex, France. e-mail: emmanuel.wagner@u-bourgogne.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the two-variable 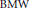$\text{BMW}$ algebra embeds into an algebra constructed from the 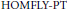$\text{HOMFLY-PT}$ polynomial. We also prove that the 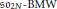$\mathfrak{s}{{\mathfrak{O}}_{2N}}-\text{BMW}$ algebra embeds in the $q$-Schur algebra of type $A$. We use these results to suggest a schema providing categorifications of the 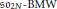$\mathfrak{s}{{\mathfrak{D}}_{2N}}-\text{BMW}$ algebra.

Keywords

57M2781R5017B3716W99tangle algebrasBMW algebraHOMFLY-PT Skein algebraq-Schur algebracategorification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 2 , 01 April 2014 , pp. 453 - 480
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Birman, J. and Wenzl, H., Braids, link polyonomials and a new algebra. Trans. Amer. Math. Soc. 313(1989), 249–273. http://dx.doi.org/10.1090/S0002-9947-1989-0992598-X Google Scholar
[2] Cautis, S., Kamnitzer, J., and Morrison, S., Webs and quantum skew howe duality. arxiv:1210.6437[math.QA]. Google Scholar
[3] Doty, S. and Giaquinto, A., Presenting Schur algebras. Internat. Math. Res. Not. 36(2002), 1907–1944.Google Scholar
[4] Hoste, J., Ocneanu, A., Millet, K., Freyd,W, A.. Lickorish, and D. Yetter, A new polynomial invariant of knots and links. Bull. Amer. Math. Soc. 12(1985), 239–246. http://dx.doi.org/10.1090/S0273-0979-1985-15361-3 Google Scholar
[5] Kauffman, L., An invariant of regular isotopy. Trans. Amer. Math. Soc. 318(1990), 417–471. http://dx.doi.org/10.1090/S0002-9947-1990-0958895-7 Google Scholar
[6] Kauffman, L., Knots and Physics. Third edition,World Scientific, River Edge, NJ, 1991.Google Scholar
[7] Kauffman, L. and Vogel, P., Link polynomials and a graphical calculus. J. Knot Theory Ramif. 1(1992), 59–104. http://dx.doi.org/10.1142/S0218216592000069 Google Scholar
[8] Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras. Invent. Math. 53(1979), 165–184. http://dx.doi.org/10.1007/BF01390031 Google Scholar
[9] Khovanov, M., Triply-graded link homology and Hochschild homology of Soergel bimodules. Internat. J. Math. 18(2007), 869–885. http://dx.doi.org/10.1142/S0129167X07004400 Google Scholar
[10] Khovanov, M. and Lauda, A., A categorification of quantum sl(n). Quantum Topol. 1(2010), 1–92. http://dx.doi.org/10.4171/QT/1 Google Scholar
[11] Khovanov, M., Erratum to A categorification of quantum sl(n). Quantum Topol. 2(2011), 97–99. http://dx.doi.org/10.4171/QT/15 Google Scholar
[12] Khovanov, M., Mazorchuk, V., and Stroppel, C., A brief review of abelian categorifications. Th. Appl. Categ. 22(2009), 479–508.Google Scholar
[13] Khovanov, M. and Rozansky, L., Matrix Factorizations and link homology. Fund. Math. 199(2008), 1–91. http://dx.doi.org/10.4064/fm199-1-1 Google Scholar
[14] Khovanov, M., Matrix Factorizations and link homology II. Geom. Topol. 12(2008), 1387–1425. http://dx.doi.org/10.2140/gt.2008.12.1387 Google Scholar
[15] Khovanov, M. and Rozansky, L., Virtual crossings, convolutions and a categorification of the SO(2N) Kauffman polynomial. J. Gökova Geom. Topol. 1(2007), 116–214.Google Scholar
[16] Mackaay, M., Stošić, M., and Vaz, P., A diagrammatic categorification of the q-Schur algebra. Quantum Topol. 4(2013), 1–75. http://dx.doi.org/10.4171/QT/34 Google Scholar
[17] Mazorchuk, V. and C. Stroppel, , Categorification of (induced) cell modules and the rough structure of generalised Verma modules. Adv. Math. 219(2008), 1363–1326. http://dx.doi.org/10.1016/j.aim.2008.06.019 Google Scholar
[18] Morrison, S., A diagrammatic category for the representation theory of Uq (sl(N)), UC Berkeley Ph.D. thesis, 2007, arxiv:0704.1503. Google Scholar
[19] Morton, H., A basis for the Birman–Wenzl algebra. arxiv:1012.3116[math.QA]. Google Scholar
[20] Murakami, H., Ohtsuki, T., and Yamada, S., HOMFLY polynomial via an invariant of colored plane graphs. Enseign. Math. 33(1998), 325–360.Google Scholar
[21] Murakami, J., The Kauffman polynomial of links and representation theory. Osaka J. Math. 24(1987), 745–758.Google Scholar
[22] Przytycki, J. and Traczyk, P., Invariants of links of Conway type. Kobe J. Math. 4(1987), 115–139.Google Scholar
[23] Ringel, C., Tame algebras and integral quadratic forms. Lecture Notes in Math. 1099, Springer, Berlin, 1984.Google Scholar
[24] Soergel, W., Kazhdan–Lusztig–Polynome und unzerlegbare Bimoduln über Polynomringen. J. Inst. Math. Jussieu 6(2007), 501–525. http://dx.doi.org/10.1017/S1474748007000023 Google Scholar
[25] Stošić, M., Indecomposable 1-morphisms of and the canonical basis of . arxiv:1105.4458v1[math.QA]. Google Scholar
[26] Wu, H., On the Kauffman–Vogel and Murakami–Ohtsuki–Yamada graph polynomials. arxiv:1107.5333[math.GT]. Google Scholar