Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-31T07:58:30.782Z Has data issue: false hasContentIssue false
  • English
  • Français

The Representation Type of Algebras and Subalgebras

Published online by Cambridge University Press:  20 November 2018

J. P. Jans
J. P. Jans*
Affiliation:
Ohio State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For A an associative algebra with identity over a field K, [A : K] < ∞, and d an integer, we define gΛ(d) to be the number of inequivalent indecomposable Λ-modules of degree d over K. Following (6), we define Λ to be of finite representation type if 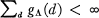. Λis said to be of bounded representation type if there exists d0 such that gΛ(d) = 0 for d ⩾ d0; Λ is of unbounded representation type if not of bounded type.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 39 - 44
Copyright
Copyright © Canadian Mathematical Society 1958

References

1. Artin, E., Galois Theory, Notre Dame Mathematical Lectures, 2 (1944).Google Scholar
2. Cartan, H. and Eilenberg, S., Homological Algebra (Princeton, 1956).Google Scholar
3. Higman, D. G., Indecomposable representations at characteristic p, Duke Math. J., 21 (1954), 377-381.Google Scholar
4. Higman, D. G., Induced and produced modules, Can. J. Math., 7 (1955), 490–508.Google Scholar
5. Jacobson, N., Lectures in Abstract Algebra (New York, 1951).Google Scholar
6. Jans, J. P. , On the indecomposable representations of algebras (forthcoming in the Annals of Mathematics),Google Scholar
7. Yoshii, T., Note on algebras of strongly unbounded representation type, Proc. Japan Acad., 32 (1956), 383-387.Google Scholar