Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thijsse, G. Philip A.
1978.
On solutions of elliptic differential equations with operator coefficients.
Integral Equations and Operator Theory,
Vol. 1,
Issue. 4,
p.
567.
Gohberg, I.
Lerer, L.
and
Rodman, L.
1978.
On canonical factorization of operator polynomials, spectral divisors and toeplitz matrices.
Integral Equations and Operator Theory,
Vol. 1,
Issue. 2,
p.
176.
Gohberg, I.
and
Rodman, L.
1979.
On the spectral structure of monic matrix polynomials and the extension problem.
Linear Algebra and its Applications,
Vol. 24,
Issue. ,
p.
157.
Rodman, Leiba
1979.
On analytic equivalence of operator polynomials.
Integral Equations and Operator Theory,
Vol. 2,
Issue. 1,
p.
48.
Gohberg, I.
Lancaster, P.
and
Rodman, L.
1979.
Perturbation Theory for Divisors of Operator Polynomials.
SIAM Journal on Mathematical Analysis,
Vol. 10,
Issue. 6,
p.
1161.
den Boer, H.
and
Thijsse, G. Ph. A.
1980.
Semi-stability of sums of partial multiplicities under additive perturbation.
Integral Equations and Operator Theory,
Vol. 3,
Issue. 1,
p.
23.
Gohberg, I
Lerer, L
and
Rodman, L
1980.
Stable factorization of operator polynomials, I. Spectral divisors simply behaved at infinity.
Journal of Mathematical Analysis and Applications,
Vol. 74,
Issue. 2,
p.
401.
Gohberg, I
Lerer, L
and
Rodman, L
1980.
Stable factorization of operator polynomials. II. Main results and applications to Toeplitz operators.
Journal of Mathematical Analysis and Applications,
Vol. 75,
Issue. 1,
p.
1.
Kaashoek, M. A.
van der Mee, C. V. M.
and
Rodman, L.
1981.
Analytic operator functions with compact spectrum. I. Spectral nodes, linearization and equivalence.
Integral Equations and Operator Theory,
Vol. 4,
Issue. 4,
p.
504.
Lancaster, P.
1981.
Minimal Factorization of Matrix and Operator Functions (H. Bart, I. Gohberg, and M. A. Kaashoek).
SIAM Review,
Vol. 23,
Issue. 4,
p.
551.
Wimmer, Harald K.
1981.
The structure of nonsingular polynomial matrices.
Mathematical Systems Theory,
Vol. 14,
Issue. 1,
p.
367.
Kaashoek, M. A.
van der Mee, C. V. M.
and
Rodman, L.
1982.
Analytic operator functions with compact spectrum. II. Spectral pairs and factorization.
Integral Equations and Operator Theory,
Vol. 5,
Issue. 1,
p.
791.
Fuhrmann, Paul A.
1982.
Feedback Control of Linear and Nonlinear Systems.
Vol. 39,
Issue. ,
p.
78.
Cohen, Nir
1983.
Spectral analysis of regular matrix polynomials.
Integral Equations and Operator Theory,
Vol. 6,
Issue. 1,
p.
161.
Fuhrmann, Paul A.
1983.
On symmetric rational transfer functions.
Linear Algebra and its Applications,
Vol. 50,
Issue. ,
p.
167.
Takahashi, Katsutoshi
1983.
On relative primeness of operator polynomials.
Linear Algebra and its Applications,
Vol. 50,
Issue. ,
p.
521.
Cohen, Nir
1983.
On minimal factorizations of rational matrix functions.
Integral Equations and Operator Theory,
Vol. 6,
Issue. 1,
p.
647.
Lerer, L
Rodman, L
and
Tismenetsky, M
1984.
Bezoutian and Schur-Cohn problem for operator polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 103,
Issue. 1,
p.
83.
Ball, Joseph A.
Gohberg, Israel
and
Rodman, Leiba
1990.
Interpolation of Rational Matrix Functions.
p.
40.
Ball, Joseph A.
Gohberg, Israel
and
Rodman, Leiba
1990.
Interpolation of Rational Matrix Functions.
p.
213.
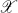 be a complex Banach space and
be a complex Banach space and 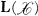 the algebra of bounded linear operators on
the algebra of bounded linear operators on 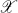 . In this paper we study functions from the complex numbers to
. In this paper we study functions from the complex numbers to 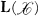 of the form
of the form