Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-01T22:32:44.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of the (р2 - 1)-Dimensional Lie Algebras of R. E. Block

Published online by Cambridge University Press:  20 November 2018

Helmut Strade
Helmut Strade*
Affiliation:
Mathematisches Seminar Universität Hamburg2000 Hamburg 13 FRG
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For all algebras G, such that 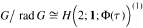is an algebra mentioned in the title, the modules of dimension ≤ p2 are determined. The module homomorphisms from the tensor product of these modules into a third module of the same type are described. We also give the central extensions of the algebras .

Keywords

17B5017B20
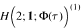Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 3 , 01 June 1991 , pp. 580 - 616
Copyright
Copyright © Canadian Mathematical Society 1991

References

[Bl-58] Block, R.E., New simple Lie algebras of prime characteristic, Trans. Amer. Math. Soc. 89(1958), 421–449.Google Scholar
[BW-88] Block, R.E. and Wilson, R.L., Classsification of the restricted simple Lie algebras, J. Algebra 114(1988), 115–259.Google Scholar
[Oeh-65] Oehmke, R.H., On a class of Lie algebras, Proc. Amer. Math. Soc. 16(1965), 1107—1113. Google Scholar
[Se] Seligman, G.B., Modular Lie Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete, 40 Springer- Verlag, 1967.Google Scholar
[Sch-60] Schafer, R.D., Nodal noncommutative Jordan algebras and simple Lie algebras of characteristic p,, Trans. Amer. Math. Soc. 94(1960), 310–326.Google Scholar
[St-77] Strade, H., Representations of the Witt algebra, J. Algebra 49(1977), 595–605.Google Scholar
[St-89/1] Strade, H., The absolute toral rank of a Lie algebra, in: G.M.Benkart and J.M.Osborn (eds), Lie algebras. Madison 1987, Lecture Notes in Math. 1373(1989), Springer Berlin-New York, 1–28.Google Scholar
[St-89/2] Strade, H., The classification of the simple modular Lie algebras: I. Determination of the two-sections,, Ann. of Math. 130(1990), 643–677.Google Scholar
[St-89/3] Strade, H., Lie algebra representations of dimension > p2 , Trans. Amer. Math. Soc. 316(1989), 1–21. [St-1] , The classification of the simple modular Lie algebras: II. The toral structure, J. Algebra, (to appear).+p2+,+Trans.+Amer.+Math.+Soc.+316(1989),+1–21.+[St-1]+,+The+classification+of+the+simple+modular+Lie+algebras:+II.+The+toral+structure,+J.+Algebra,+(to+appear).>Google Scholar
[St-2] Strade, H., The classification of the simple modular Lie algebras: III. Solution of the classical case, Ann. of Math, (to appear).Google Scholar
[St-3] Strade, H., New methods for the classification of the simple modular Lie algebras, Mat. Sbornik 181(1990), 1391–1402.Google Scholar
[St-4] Strade, H., The classification of the simple modular Lie algebras: IV. The determination of the associated graded algebra, submitted.Google Scholar
[SF-88] Strade, H. and Farnsteiner, R., Modular Lie algebras and their representations. Marcel Dekker Textbooks and Monographs 116, 1988.Google Scholar
[W-76] Wilson, R.L., A structural characterization of the simple Lie algebras of generalized Cartan type over fields of prime characteristic, J. Algebra 40(1976), 418–465.Google Scholar